고역통과필터

목차

1.필터란?

2.고역 통과 필터

3.필터의 종류

4.수동소자 필터

5.1차 함수와 1차 회로

본문내용

사인파를 저지시키고, 고주파의 사인파를 통과시키는 데 사용된다. 우리는 저지 대역( < c)과 통과 대역 ( > c)를 구분하기 위해 차단 주파수 c를 사용한다. 이상적인 고역-통과 여파기는 그림 9-4에 보인 크기 곡선과 위상 곡선으로 특징지어진다. 저지 대역에서의 크기 함수가 0이므로, 그곳에서의 위상 특성의 모양은 중요하지 않다.
이와 같은 이상적인 고역-통과 특성을 갖는 회로를 실현하는 것은 불가능하다. 실제의 회로들은 이상적인 고역-통과 특성에 근사한 특성을 나타낸다. 전달 함수의 차수가 높으면 높을수록, 회로의 특성이 이상적인 특성에 가까워질 것이다. 그러나, 전달 함수의 차수를 높이면, 회로를 적절히 동작시키기 위해 조정해야 할 부품의 수가 훨씬 많아지므로, 실제로 회로를 실현하는 것이 그만큼 어려워진다. 여기서 우리는, 1차 및 2차 함수들과 회로들에 대해서만 논의할 것이다.
1차 함수와 1차 회로
1차 고역-통과 함수는 다음과 같이 주어진다.
T1(s) =
{ s} over {s+ c }
=
{ s/ c} over {s/ c + 1 }
이 함수가 이상적인 고역-통과 특성을 근사한 것인지를 알아 보기 위해,
s = j 로 놓은 다음, 크기 함수와 위상 함수를 구하면
T1(j ) =
{ j / c} over {j / c + 1 }
T1(j ) =
{ / c} over {SQRT { 1 + {( / c) }^{ 2}} }
1( ) =
{ } over {2 }
{ - tan}^{-1}[{ } over { c }]
가 얻어질 것이다.
(a) (b)
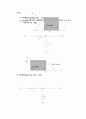
그림 1-3
이들 두 함수를 그림 1-3(a)와 (b)에 각각 도시해면 그림 1-3(a)에서, 크기 함수의 특성이 저지 대역과 통과 대역을 주파수에 따라 명확히 구분지울 수 있는 급격한 크기의 상승을 보이지는 않는다는 점에 유의하기 바란다. 그럼에도 불구하고, 주파수가 무한대일 때의 크기 값의 1/
SQRT { 2}
배 되는 크기를 갖는 주파수 즉 c를 우리는 차단 주파수 또는 반전력 주파수로 간주한다. c의 단위가 라디안/초 이므로, 헤르치 단위의 차단 주파수는 fc = c/2 로 주어진다. 차단 주파수는 저지 대역폭을 나타내기도 한다. 그림 9-5(b)는 고역-통과 함수의 위상 특성이 점진적으로 0에 접근한다는 것을 보여준다. 따라서, 만일 우리가 이상적인 위상-특성 곡선에서 k와 곡선의 기울기 모두를 0으로 취한다면, 위상 곡선은 통과 대역내에서 이상적인 위상 곡선과 비슷해질 것이다.
T1(s) =
{ s} over {s+{ }_{c } }
=
{ s/{ }_{c }} over {s/{ }_{c }+1 }
식으로 주어진 1차 고역-통과 함수는 그림 1-3에 보인 두 회로망으로 실현할(1보다 작은 스케일 인수로)수 있을 것이다. 이들 두 회로망은 모두 입력 저항 Rs와 부하 저항 RL 사이에서 동작하며, 다음의 전달 함수로 표현된다.
T(s) =
{ V0} over {Vi }
=
{ RL} over {Rs + RL }
(
{ s} over {s + c }
)
(a) (b)
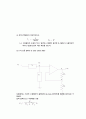
그림 1-4
여기서,
c =
{1 } over {(Rs +RL)C }
(RC회로)
c =
{RsRL } over {Rs + RL }
{1} over {L }
(RL회로)
이다. 이 식들은, 입력 저항과 부하 저항이 주어졌거나 이미 알고 있을 경우, 특정한 차단 주파수를 얻기 위한 C의 값[그림 9-5(a)의 회로의 경우]또는 L의 값[그림 1-4(b)의 회로의 경우]을 구하는 데 사용된다. 스케일 인수 RL/(Rs+RL)은 모든 주파수에 대해 동등하게 영향을 미치므로, 특성 곡선의 모양을 변형시키지 않을 것이다. 다만, 그 값이 1보다 작기 때문에, 통과대역내의 신호를 감쇠시키기만 할 것이다(저지 대역내의 신호도 같이 감쇠된다). 만일 1차 함수로 실현한 고역-통과 특성이 우리가 원하는 특성에 만족할만한 근사를 보이지 못한다면, 우리는 2차 또는 그 이상의 차수의 함수를 사용해야 할 것이다.
2차 함수와 2차 회로
많은 2차 함수들이 고역-통과 특성을 보인다. 이 함수들은 그들의 저지-대역 특성과 통과-대역 특성에서 약간 차이가 있다. 널리 사용되는 함수들 중의 하나가
T2(s) =
{s}^{2 } over {s^{2} + s SQRT {2} c + c^{2 } }
이다.
이 식과 연관된 크기 함수와 위상 함수는 s = j 로 놓음으로써 구해진다.
즉,
T2(j )=
{- ^{2 } } over {( c^{2 }- ^{2 }) + j SQRT {2 } c }
=
{( / c)^{2 } } over {[( / c)^{2 } - 1] - j SQRT {2 }( / c)}
T2(j ) =
{ ( / c)^{2 }} over {SQRT { {[ ( / c)^{2 } - 1] }^{2 }+2{( / c)}^{2 }} }= { ( / c)^{2 }} over {SQRT { 1+{( / c) }^{ 4}} }
2( ) =
{ -tan}^{-1}[{ SQRT { 2}( / c)} over { { ( / c)}^{2 } - 1 }]
=
{ -tan}^{-1}[{ SQRT { 2}( / c)} over {1- { ( / c)}^{2 } }]
이 함수들을 그림 1-5(a)와 (b)에 각각 도시했다. 그림 9-6(a)에서, 상수 c가 = 때의 크기의 1/
SQRT {2 }
배 되는 크기를 갖는 주파수를 가리키며, 이 상수가 차단 주파수 또는 저지 대역폭을 나타내는 데 사용된다는 점에 다시 한번 주목하기 바란다. 한편, 그림 1-5(b)는, 위상 특성이 주파수가 커짐에 따라 점진적으로 0에 접근한다는 것을 보여준다.
그림 1-5
이 2차 함수와 1차 함수의 크기 특성을 비교해 나타냈다.저지 대역에서는 2차 함수의 특성 곡선이 1차 함수의 특성 곡선보다 더 아래에 있고 (따라서, 2차 함수가 입력 신호를 더 많이 감쇠시킨다).통과 대역에서는 2차 함수의 특성 곡선이 1차 함수의 특성 곡선보다 더 위에 있다(따라서, 2차 함수가 입력 신호를 더 잘 통과시킨다)는 점에 주목하기 바란다.

키워드

필터,   고주파,   부하,   수동소자,   1차 회로,   주파수