컴파일러 5장 연습 문제

목차

5.1 다음 괄호에 알맞은 단어를 쓰시오.
5.2 다음 약어에 대한 원어(full name)를 쓰시오.
5.3 다음을 간략히 정의하시오.
5.4 다음을 간단히 설명하시오
5.5 Mini C 언어에 대한 다음 구조를 문법 흐름도로 그리시오.
5.6 다음과 같은 문법이 주어졌을 때, 문장 begin d;s;s end 에 대한 좌측 유도와 우측 유도 과정을 보이시오.
5.7 생성 규칙이 다음과 같은 문법이 있다.
중략..

본문내용

), $LSLS )
┣ {q, ()), $LSLSRS)
┣ {q, ()), $LSS )
┣ {q, ()), $LS )
┣ {q, )), $LSLS )
┣ {q, ), $LSLSRS)
┣ {q, ), $LSS )
┣ {q, ), $LS )
┣ {q, ε, $LSRS )
┣ {q, ε, $S )
┣ {q, ε, ε )
5.27 다음 context-free 언어를 보고 물음에 답하시오.
L = { ωcωR | ω∈{a,b}* }
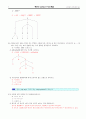
① L을 인식하는 PDA P를 top-down 방법으로 구성하시오.
G : S → aSa | bSb | c
① 다른 방법
P = 동일하고 전이함수만 변경함
δ(q1, a, S) = (q1, Sa)
δ(q1, b, S) = (q1, Sb)
δ(q1, c, S) = (q2, ε)
δ(q2, a, a) = (q2, ε)
δ(q2, b, b) = (q2, ε)
δ(q2, ε, R) = (q2, ε)
② 인식과정
(q1, abbcbba, SR)
┣ (q1, bbcbba, SaR)
┣ (q1, bcbba, SbaR)
┣ (q1, cbba, SbbaR)
┣ (q2, bba, bbaR)
┣ (q2, ba, baR)
┣ (q2, a, aR)
┣ (q2, ε, R)
┣ (q2, ε, ε)
P = ( {q1, q2}. {a, b, c}, {a, b, S, R}, δ, q1, SR, {q2} ),
δ(q1, ε, S) = { (q1, aSa) , (q1, bSb) }
δ(q1, a, aS) = (q1, S) δ(q1, b, bS) = (q1, S)
δ(q1, c, S) = (q2, ε)
δ(q2, a, a) = (q2, ε)δ(q2, b, b) = (q2, ε)
δ(q2, ε, R) = δ(q2, ε)
② P에 의해서 스트링 abbcbba를 인식하는 과정을 보이시오.
(q1, abbcbba, SR)┣ (q1, abbcbba, aSaR)
┣ (q1, bbcbba, SaR)
┣ (q1, bbcbba, bSbaR)
┣ (q1, bcbba, SbaR)
┣ (q1, bcbba, bSbbaR)
┣ (q1, cbba, SbbaR)
┣ (q2, bba, bbaR)
┣ (q2, ba, baR)
┣ (q2, a, aR)
┣ (q2, ε, R)
┣ (q2, ε, ε)
③ L을 인식하는 PDA R을 bottom-up 방법으로 구성하시오.
P = ( {q1, q2}. {a, b, c}, {a, b, $}, δ, q1, $, {q2} ),<참조 ex27>
δ(q1, a, ε ) = (q1, a)δ(q1, b, ε ) = (q1, b)
δ(q1, c, ε ) = (q2, ε)
δ(q2, a, a ) = {(q2, ε)}δ(q2, b, b ) = {(q2, ε)}
δ(q2, ε, $ ) = {(q2, ε)}
④ R에 의해서 스트링 abbcbba를 인식하는 과정을 보이시오.
(q1, abbcbba, $)┣ (q1, bbcbba, $a)
┣ (q1, bcbba, $ab)
┣ (q1, cbba, $abb)
┣ (q2, bba, $abb)
┣ (q2, ba, $ab)
┣ (q2, a, $a)
┣ (q2, ε, $)
┣ (q2, ε, ε)
5.28 다음 언어 ( ∑ = {a, b, c} )를 인식하는 PDA를 구성하시오.
① L = { anb2n | n≥0 }
G :S → aSbb | ε
P = ( {q, r}, {a, b}, {a, b, S}, δ, q, S, {r} ),
δ(q, ε, S) = { (q, aSbb), (r, ε) }
δ(q, a, aS) = (q, S)
δ(q, b, Sb) = (r, ε)
δ(r, b, b) = (r, ε)
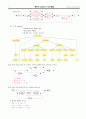
② L = { ω | na(ω) = nb(ω) }
G :S → aSb | bSa
P = ( {q}, {a, b}, {a, b, $}, δ, q, $, φ ),
δ(q, a, a) = (q, aa)
δ(q, a, b) = (q, ε)
δ(q, b, b) = (q, bb)
δ(q, b, a) = (q, ε)
δ(q, ε, $) = (q, ε)
③ L = { ω | na(ω) + nb(ω) = nc(ω) }
PDA P = ( { q }, { a, b, c }, { a, b, c, $ }, δ, q, $, φ ),
δ(q, a, $) = (q, a$)δ(q, b, $) = (q, b$)δ(q, c, $) = (q, c$)
δ(q, a, a) = (q, c)δ(q, b, a) = (q, c)δ(q, c, a) = (q, ac)
δ(q, a, b) = (q, c)δ(q, b, b) = (q, c)δ(q, c, b) = (q, bc)
δ(q, a, c) = (q, ac)δ(q, b, c) = (q, bc)δ(q, c, c) = (q, ε)
δ(q, ε, $) = {q, ε)
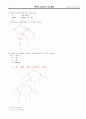
5.29 다음을 CFG로 고안하고 주어진 스트링에 대한 유도 트리를 그리시오.
① list structure :
▷ λ는 null을 나타내고 a는 atom을 나타내는 리스트 구조이다. 그리고 ℓ1, ℓ2, …, ℓk 가 리스트 구조이면, (ℓ1, ℓ2, …, ℓk)도 역시 리스트 구조이다.
▷ (((a,a),λ,(a)),a)
② nested parenthesis structure :
△ 괄호의 종류는 () 과 [] 의 두 가지이며, 항상 균형을 이룬다. 그러나 상식적으로 ([])와 ([[]])는 가능한 구조이나 ([)나 (])은 틀린 형태이다.
△ ([][])[()]
G : S → (S)S | [S]S | ε
유도과정 :
S ⇒ (S)S ⇒ ([S]S)S ⇒ ([S][S]S)S ⇒ ([S][S]S)[S]S ⇒ ([S][S]S)[(S)S]S
5.30 다음은 Tiny C (by Ian Kaplan) 문법을 EBNF로 기술한 것이다. 2개의 정수를 매개 변수로 받아 최대 공약수(GCD: Greatest Common Divisor)를 구하는 함수 gcd()를 작성하시오.
5.31 다음은 SPL (Simple Programming Language)의 문법을 EBNF로 기술한 것이다. N개의 정수 자료를 읽어 최소 값과 최대 값을 찾아 출력하는 SPL 프로그램을 작성하시오. 첫 번째 읽은 값이 자료의 개수이다.

키워드

컴파일러,   컴파일러 입문,   연습문제