본문내용
49
2.72
갈 색
A
65
64
1
1
0.02
갈 색
B
50
36
14
196
5.44
갈 색
O
40
48
-8
64
1.33
갈 색
AB
5
12
-7
49
4.08
합 계
400
400
0
18.12
분산분석(analysis of variance : ANOVA)
: 두 평균을 검정하는 데 사용하는 검정이 확장된 형태의 검정기법
개의 모집단에서 각각 표본을 독립적으로 뽑아 개의 독립인 표본을 사용하여 모집단을 비교하는 것이 분산분석의 목적이다.
분산분석은 각 표본에서 구한 개 표본평균들의 차이가 오차에 의한 것으로 생각할 수 있을 만큼 작은 것인지, 아니면 그 차이가 오차에 의한 것으로 보기에는 너무 커서 각 표본이 서로 다른 모집단에서 추출되었다고 보아야 하는지를 판단하는데 사용
일원배치법(one-way classification)
: 관찰치가 단 하나의 분류기준에 근거하여 여러 처리군으로 나누어지는 경우
분산분석법을 적용하기 위해서는 몇 가지 기본적인 가정이 필요
각 표본은 확률표본이고, 서로 독립이라고 가정
확률변수는 정규분포를 따르고, 그 분포의 분산이 일정하다고 가정한다.
표본평균들이 매우 작은 차이를 보이면, 가 사실일 가능성이 크다고 생각하고, 표본평균들이 차이가 크면 보다는 가 사실일 가능성이 더 크다고 생각할 수 있다.
가설검정과정에서 표본 평균간의 차이 뿐만아니라 각 표본 내의 변동도 고려해야만 한다.
표본 평균간의 변동이 표본내의 변동에 비해서 클 때 대립가설을 받아들여야 되겠다는 생각을 가질 수 있다. 그러나 어느 정도로 커야 대립가설을 받아들이느냐 하는 기준 설정이 필요.
급내 변도 또는 급내 제곱합(within sum of squares)
각 표본이 동일한 관찰치의 개수 으로 구성된다고 가정한다.
관찰치 : (는 모집단, 는 모집단의 번째 관찰치)
전체평균 , , ,
모분산에 대한 불편 추정치
, ,
분산 의 분편 추정치
⇒
오차제곱합(error sum of squares ; SSE) or 제곱합(within sum of squares)
SSE의 자유도 :
급간제곱합(between sum of squares)
가 참이고 각 모집단의 분산이 동일하면 개의 표본들을 평균 및 분산 을 갖는 동일한 모집단에서 추출한 하나의 커다란 표본으로 간주할 수 있다.
의 분산
; 표본평균의 분산에 관한 불편추정치
의 불편추정치 ; 귀무가설이 참일 경우의 의 또 다른 불편추정치의 분산 이므로 의 추정치
평균간제곱합(sum of squares between means) or 근간제곱합(between sum of squares ; SSB)
가설검정
귀무가설이 참이면 두 개의 추정치 와 는 의 분편추정치이고 비슷한 값을 갖게 된다.
이를 비교하기 위하여 분산비(ratio of variance)를 사용한다.
⇒ 이 통계량은 자유도 을 갖는 분포를 한다.
이 분산비가 1에서 약간 벗어나는 것은 우연 변동으로 들릴 수 있으나, 분산비가 1보다 훨씬 크면 의 타당성에 의심을 품게 된다.
⇒ 가 참이 아니면 은 실험오차뿐만 아니라 모집단 평균간 실질적인 차이에 의해서도 영향을 받으므로 은 을 과대추정하는 경향이 있다.
분산분석표
귀무가설이 참이면 의 또다른 추정치
, (은 총 관찰치의 개수)
총제곱합(total sum of squares ; SST) :
SST의 자유도 :
SST의 자유도는 SSB와 SSE의 자유도의 합이다.
평균제곱(means square) : 제곱합을 자유도로 나눈 제곱합의 평균
일반적인 분산분석
모집단이 개이고 표본의 크기도 같지 않은 경우
개의 독립인 표본들의 크기를 각각 라 하면...
표본1
표본2
표본
…
…
…
표본 크기
표본 총계
표본 평균
…
…
…
; 번째 모집단의 번째 관찰치
오차항 는 서로 독립이고 모두 을 따르는 확률변수라고 가정하면,는 을 따른다.
이제 다음의 귀무가설을 검정하자.
귀무가설 ;
대립가설 ; 적어도 두 개 이상의 모평균은 다르다
제곱합을 정의하자
(총 제곱합)
(급간 제곱합)
(급내 제곱합)
는 총평균으로 (은 관찰치의 총수로 이다)
는 번째 표본의 평균으로 , 이다.
자유도
, ,
의 자유도는
의 자유도는
의 자유도는
제곱합을 계산할 때 보통 다음과 같이 변형된 식을 사용한다.
여기서
수정항(correction term) ;, (번째 표본의 총합)
변 인
급 간
급 내
전 체
F의 값이 크면 클수록 대립가설이 참일 가능성이 높아지는데, 의 분포는 하에서 자유도가 인 분포라는 것이 알려져 있으므로 검정기준은 아래와 같이 된다.
일 때 를 기각한다.
예제) 어느 한 작업자의 생산성이 일주일(5일)동안에 변함이 없는지를 검정하기 위해, 그 작업자에게는 알리지 않고 고용주가 표에서 보는 바와 같이 18일을 임의로 택하여 기록하였다.(생산성은 작업자가 생산한 품목의 경상 시장가격으로 측정하였다.) 에서 검정하라.
요일별 15일간의 생산성
월
화
수
목
금
143
128
110
162
136
144
158
160
132
180
160
138
138
168
120
110
130
135
표본 크기
표본 합계
표본 평균
3
381
127
4
600
150
4
770
154
3
426
142
3
375
125
풀이) 먼저 작업자의 생산성은 동일한 분산을 갖는 정규분포를 따르고, 그의 매일 매일의 생산성은 다음날의 생산성에 여향을 미치지 않는다고 가정한다. 검정 절차는 다음과 같다.
1.
2. : 적어도 두 개의 평균은 같지 않다. 즉 적어도 두 요인 간의 평균 생산성은 서로 다르다.
3. 계산과정
변 인
급 간
2517
4
629.3
2.05
급 내
4000
13
307.7
전 체
6517
17
4. 자유도가 (4,13)이므로 이다. 따라서, 분산비값이 3.18보다 크면 를 기각한다.
5. 분산분석표에서 계산된 값이 2.05이므로 를 기각하지 않는다.즉, 작업자의 평균 생산성이 5일 동안에 서로 다름을 입증할 수 없다.
분포 : 두 정규모집단의 분산을 비교하거나 분산분석 등에 사용
정의 : , ; 과 는 독립
⇒ ; 자유도(, )인 분포
자유도에 따른 분포의 밀도함수 변화
일 때
일 때
일 때
2.72
갈 색
A
65
64
1
1
0.02
갈 색
B
50
36
14
196
5.44
갈 색
O
40
48
-8
64
1.33
갈 색
AB
5
12
-7
49
4.08
합 계
400
400
0
18.12
분산분석(analysis of variance : ANOVA)
: 두 평균을 검정하는 데 사용하는 검정이 확장된 형태의 검정기법
개의 모집단에서 각각 표본을 독립적으로 뽑아 개의 독립인 표본을 사용하여 모집단을 비교하는 것이 분산분석의 목적이다.
분산분석은 각 표본에서 구한 개 표본평균들의 차이가 오차에 의한 것으로 생각할 수 있을 만큼 작은 것인지, 아니면 그 차이가 오차에 의한 것으로 보기에는 너무 커서 각 표본이 서로 다른 모집단에서 추출되었다고 보아야 하는지를 판단하는데 사용
일원배치법(one-way classification)
: 관찰치가 단 하나의 분류기준에 근거하여 여러 처리군으로 나누어지는 경우
분산분석법을 적용하기 위해서는 몇 가지 기본적인 가정이 필요
각 표본은 확률표본이고, 서로 독립이라고 가정
확률변수는 정규분포를 따르고, 그 분포의 분산이 일정하다고 가정한다.
표본평균들이 매우 작은 차이를 보이면, 가 사실일 가능성이 크다고 생각하고, 표본평균들이 차이가 크면 보다는 가 사실일 가능성이 더 크다고 생각할 수 있다.
가설검정과정에서 표본 평균간의 차이 뿐만아니라 각 표본 내의 변동도 고려해야만 한다.
표본 평균간의 변동이 표본내의 변동에 비해서 클 때 대립가설을 받아들여야 되겠다는 생각을 가질 수 있다. 그러나 어느 정도로 커야 대립가설을 받아들이느냐 하는 기준 설정이 필요.
급내 변도 또는 급내 제곱합(within sum of squares)
각 표본이 동일한 관찰치의 개수 으로 구성된다고 가정한다.
관찰치 : (는 모집단, 는 모집단의 번째 관찰치)
전체평균 , , ,
모분산에 대한 불편 추정치
, ,
분산 의 분편 추정치
⇒
오차제곱합(error sum of squares ; SSE) or 제곱합(within sum of squares)
SSE의 자유도 :
급간제곱합(between sum of squares)
가 참이고 각 모집단의 분산이 동일하면 개의 표본들을 평균 및 분산 을 갖는 동일한 모집단에서 추출한 하나의 커다란 표본으로 간주할 수 있다.
의 분산
; 표본평균의 분산에 관한 불편추정치
의 불편추정치 ; 귀무가설이 참일 경우의 의 또 다른 불편추정치의 분산 이므로 의 추정치
평균간제곱합(sum of squares between means) or 근간제곱합(between sum of squares ; SSB)
가설검정
귀무가설이 참이면 두 개의 추정치 와 는 의 분편추정치이고 비슷한 값을 갖게 된다.
이를 비교하기 위하여 분산비(ratio of variance)를 사용한다.
⇒ 이 통계량은 자유도 을 갖는 분포를 한다.
이 분산비가 1에서 약간 벗어나는 것은 우연 변동으로 들릴 수 있으나, 분산비가 1보다 훨씬 크면 의 타당성에 의심을 품게 된다.
⇒ 가 참이 아니면 은 실험오차뿐만 아니라 모집단 평균간 실질적인 차이에 의해서도 영향을 받으므로 은 을 과대추정하는 경향이 있다.
분산분석표
귀무가설이 참이면 의 또다른 추정치
, (은 총 관찰치의 개수)
총제곱합(total sum of squares ; SST) :
SST의 자유도 :
SST의 자유도는 SSB와 SSE의 자유도의 합이다.
평균제곱(means square) : 제곱합을 자유도로 나눈 제곱합의 평균
일반적인 분산분석
모집단이 개이고 표본의 크기도 같지 않은 경우
개의 독립인 표본들의 크기를 각각 라 하면...
표본1
표본2
표본
…
…
…
표본 크기
표본 총계
표본 평균
…
…
…
; 번째 모집단의 번째 관찰치
오차항 는 서로 독립이고 모두 을 따르는 확률변수라고 가정하면,는 을 따른다.
이제 다음의 귀무가설을 검정하자.
귀무가설 ;
대립가설 ; 적어도 두 개 이상의 모평균은 다르다
제곱합을 정의하자
(총 제곱합)
(급간 제곱합)
(급내 제곱합)
는 총평균으로 (은 관찰치의 총수로 이다)
는 번째 표본의 평균으로 , 이다.
자유도
, ,
의 자유도는
의 자유도는
의 자유도는
제곱합을 계산할 때 보통 다음과 같이 변형된 식을 사용한다.
여기서
수정항(correction term) ;, (번째 표본의 총합)
변 인
급 간
급 내
전 체
F의 값이 크면 클수록 대립가설이 참일 가능성이 높아지는데, 의 분포는 하에서 자유도가 인 분포라는 것이 알려져 있으므로 검정기준은 아래와 같이 된다.
일 때 를 기각한다.
예제) 어느 한 작업자의 생산성이 일주일(5일)동안에 변함이 없는지를 검정하기 위해, 그 작업자에게는 알리지 않고 고용주가 표에서 보는 바와 같이 18일을 임의로 택하여 기록하였다.(생산성은 작업자가 생산한 품목의 경상 시장가격으로 측정하였다.) 에서 검정하라.
요일별 15일간의 생산성
월
화
수
목
금
143
128
110
162
136
144
158
160
132
180
160
138
138
168
120
110
130
135
표본 크기
표본 합계
표본 평균
3
381
127
4
600
150
4
770
154
3
426
142
3
375
125
풀이) 먼저 작업자의 생산성은 동일한 분산을 갖는 정규분포를 따르고, 그의 매일 매일의 생산성은 다음날의 생산성에 여향을 미치지 않는다고 가정한다. 검정 절차는 다음과 같다.
1.
2. : 적어도 두 개의 평균은 같지 않다. 즉 적어도 두 요인 간의 평균 생산성은 서로 다르다.
3. 계산과정
변 인
급 간
2517
4
629.3
2.05
급 내
4000
13
307.7
전 체
6517
17
4. 자유도가 (4,13)이므로 이다. 따라서, 분산비값이 3.18보다 크면 를 기각한다.
5. 분산분석표에서 계산된 값이 2.05이므로 를 기각하지 않는다.즉, 작업자의 평균 생산성이 5일 동안에 서로 다름을 입증할 수 없다.
분포 : 두 정규모집단의 분산을 비교하거나 분산분석 등에 사용
정의 : , ; 과 는 독립
⇒ ; 자유도(, )인 분포
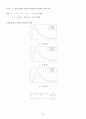
자유도에 따른 분포의 밀도함수 변화
일 때
일 때
일 때





















































소개글