RC미분적분회로예비보고서

소개글

RC미분적분회로예비보고서에 대한 보고서 자료입니다.

목차

1 실험 제목

2. 실험 목적

3. 기초 이론

4. 실험 방법 회로

본문내용

sin PHI)sin omega t=0
가 모든 t에서 성립되기 위해서는 위의 두식이 성립해야하고, 위의 두식으로 부터.
PHI
를 구해낼 수 있다. 즉,
{1}over{omegaC}cos PHI=R sin PHI
tan PHI={sin PHI}over{cos PHI}={1}over{R omega C}
와 같고, 이 식에 따라,
PHI=arctan{1}over{R omegaC}
이 된다.
{I}_{p}
를 구하기 위해서는
PHI
의 결과를
R cos PHI + {1}over{omegaC}sin PHI -{{V}_{p}}over{{I}_{p}}=0
에 대입하고, 이 식을 정리하면,
R{R}over{ SQRT {{R}^{2}+{({1}over{omegaC})}^{2} } }+{1}over{omegaC}{{1}over{omegaC}}over{SQRT{{R}^{2}+{({1}over{omegaC})}^{2}}}={{V}_{p}}over{{I}_{p}}=0
이된다.
이에따라
{I}_{p}={{V}_{p}}over{SQRT{{R}^{2}+{({1}over{omegaC})}^{2}}}
식이 유도된다.
따라서, 회로내에 흐르게 되는 전류는,
i={{V}_{p}}over{SQRT{{R}^{2}+{({1}over{omegaC})}^{2}}}sin(omegat+ PHI)
이다.
저항에 걸리는 출력전압은 다음과 같이 되며,
{v}_{o}=R{I}_{p}sin(omegat+PHI)
이 식을 이용하여 입력전압의 rms값에 대한 출력전압의 비를 나타내면,
{{V}_{o}}over{{V}_{i}}={1}over{SQRT{1+{({1}over{omegaRC})}^{2}}}
와 같이 된다.
이러한 RC직렬회로에서 저항과 커패시턴스 값이 상당히 작아 입력된 주파수 범위 내에서
omega R C<<1
이 성립한다고 본다면, 이때의 출력전압은 위에 계산된 식들을 이용하여,
{v}_{o}={V}_{p}omegaRCsin(omegat+{pi}over{2})={V}_{p}omegaRCcos omegat
이다.
또한 이것을 입력신호의 시간에 대한 도함수를 표현할 수있다.
{d{v}_{i}}over{dt}=omega{V}_{p}cos omegat
위의 두 식을 결합하게 되면,
{v}_{o}=RC{d{v}_{i}}over{dt}
가 된다. 즉,
omega RC<<1
의 조건이 있을경우에는 RC필터회로에서의 저항에서의 출력 전압은 입력전압의 도함수의 꼴이 된다. 이를 이용하여 RC필터회로를 가지고 입력전압의 미분치를 구할수 있는 것이다. 따라서
{v}_{c}>>{v}_{o}
의 조건이 충족되어야 RC회로가 보다 정확한 미분동작을 하기 때문에 커패시터의 용량성 리액턴스값을 이 조건에 충족시키려면 용량이 작은 커패시터를 사용하고(용량성 리액턴스는 커패시터의 용량에 반비례하므로) 저항은 그 값이 아주 작은 것을 사용한다면 보다 정밀한 미분회로를 꾸밀 수 있는 것이다.
3) 적분회로
RC회로에서 저항에서 출력되는 전압은 미분동작을 하는 반면, 커패시터에 걸리는 출력전압을 생각해 보면,
i={dq}over{dt}=C{dv}over{dt}
에 의해 흐르는 전류의 적분이 된다. 즉,
{v}_{c}={1}over{C} INT {I}_{p}sin (omegat+PHI)dt=-{{I}_{p}}over{omegaC}cos (omegat+PHI)
와 같다. 여기서 R과C를 매우 크게하면
omegaRC>>1
이 되며, 이때는
{I}_{p}={{V}_{p}}over{R},PHI=0
이므로, 위 식은,
{v}_{c}=-{{V}_{p}}over{RC omega}cos omegat
이 된다. 이 식과 입력전압의 정의식,
{v}_{i}={V}_{p}sin omegat
을 이용하여
{v}_{c}=-{{V}_{p}}over{RC omega}cos omegat
식을 정리하면 다음과 같이 나타낼 수 있다.
{v}_{c}={1}over{RC} INT {v}_{i}dt
즉 커패시터에서의 출력전압은 입력전압의 적분값이다. 이때에도 역시 미분회로와 마찬가지로
{V}_{R}>>{V}_{o}
의 조건이 충족되어야 한다, 즉 이 조건을 충족시키기 위해서는 큰 용량의 커패시터(용량성 리액턴스와 커패시터의 용량은 반비례관계에 있으므로)와 큰 값의 저항을 사용하면 된다.
4. 실험 방법. 및 회로
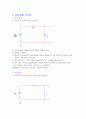
1. 미분회로
1) 이론과 맞게 회로도를 작성한다.
2) 주파수 1kHz, 최대진폭 5V의 정현파 파형을 만든다.
3) 파형을 기록한다.
4) 회로에서 저항에서의 출력전압의 파형을 관찰하고, 이를 종이에 기록하여 입력
전원의 미분치인지 알아본다.
5) 파형 발생기로 주파수 1kHz, 최대진폭 5V인 구형파를 발생시킨다.
6) 위와 같은 과정으로 입력전압의 파형과 회로의 저항에서의 출력저항의 파형
을 비교하여 실제 미분이 이루어지는지 관찰한다.
7)PSPICE로 회로도를 작성하고 시뮬레이션 한다.
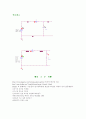
2. 적분회로
1) 이론에 맞게 다음과 같이 회로도를 작성한다..
2) 파형발생기를 이용하여 주파수 1kHz, 최대진폭 5V의 정현파를 발생시킨다.
3) 파형을 기록한다.
4) 오실로스코프를 이용하여 커패시터에서의 출력전압의 파형을 관찰, 기록한
입력전압의 파형과 비교하여 실제 적분이 이루어 졌는지 관찰한다.
5) 주파수 1kHz, 최대진폭 5V의 구형파를 발생시킨 후, 위와 같은 과정을 거쳐
실제 적분이 이루어지는지 관찰한다.
6) PSPICE로 작성한 회로도를 가지고 시뮬레이션 한다.
미분회로
적분회로
◈참 고 문 헌◈
http://www.eleparts.co.kr/html/p_index/cap.html 캐패시티에관한 내용
http://user.chollian.net/~kimjh94/junja/junja_7/junja7-2.html
Pspice 와 함께하는 기초전자 전기공학실험 홍순관 박진홍 이영석 공저 홍릉출판사
신전기학 김의균. 박세환
전기이론 김응목 지문사
전자물리학 실험 박태영 원광대학교출판국
대학전자물리실험 최경석 김태진 塔出版社 1981
전자통신 기초 실험 연규호저
대학물리학 김용은 대웅

키워드

RC,   RC미분,   RC적분,   캐패시터,   Capacitor,   RC직렬회로