목차
MATLAB 개요와 응용
10장 수치해석
일변수 방정식의 풀이
함수의 최소값 또는 최대값 구하기
수치적분
상미분 방정식
응용예제
일변수 방정식의 풀이
함수의 최소값 또는 최대값 구하기
수치적분
상미분 방정식
응용예제
본문내용
과학과 공학에서 식으로 표현된 수학 문제에서 정확한 해를 얻기가 어렵거나 불가능한 경우에는 일반적으로 수치적인 방법들을 사용한다.
MATLAB은 광범위한 수학문제들을 수치적으로 풀기 위한 많은 함수 라이브러리를 가지고 있는데, 이 장에서는 이러한 함수들 중에서 가장 빈번하게 사용되는 함수들의 사용방법에 대해 설명한다.
여기서는 MATLAB의 사용방법에 대해 설명하며, 수치해석에 대한 자세한 사항은 수치해석 관련 책을 참조하도록 한다.
이 장에서는 미지수가 한 개인 방정식의 풀이, 함수의 최소값 또는 최대값 구하기, 수치적분, 일차 상미분방정식 등의 주제들을 다룬다.
일변수 방정식 f(x)=0의 해는 함수가 x축과 교차하는(함수 값이 0이 되는) 값, 또는 함수의 부호가 바뀌는 값이다.
정확한 해는 함수의 값이 정확히 0이 되는 x의 값이다. 만일 이러한 값이 존재하지 않거나 구하기 어렵다면, 함수의 부호가 바뀌는, 즉 축과 교차하는 점에 매우 근접한 수치해 x를 구한다. 수치해는 반복과정을 통해 해에 더 가까운 x 값을 구하며, 반복을 해도 더 이상 해가 어떤 한도보다 변하지 않으면 더 이상의 반복을 중지한다.
MATLAB에서 함수의 영점(zero)은 명령어 fzero를 이용하여 구한다:
해를 구할 함수인 입력인자 function의 입력 방법
수학식을 문자열로 입력하는 방법.
ex) x=fzero('x^2-2*x-3', 2)
함수를 함수 파일에서 사용자정의 함수로 만든 다음, 이 함수의 핸들을 입력하는 방법. ex) func.m 파일에 함수가 정의되어 있을 때, x=fzero(@func, 2)
함수를 먼저 익명함수로 정의한 다음, 이 익명함수의 이름을 입력하는 방법.
함수는 표준 형태로 쓴다. 예) 식이 xe-x=0.2 일 때, 'x*exp(-x)-0.2'와 같이 입력.
함수를 문자열로 입력하는 경우, 미리 정의된 변수는 식에 포함될 수 없다.
ex) b=0.2가 정의되어 있을 때, 'x*exp(-x)-b'의 입력은 허용되지 않는다.
x0는 스칼라 또는 두 원소의 벡터가 될 수 있다.
x0가 스칼라인 경우: 함수가 x축과 교차하는 점 근처의 x 값을 x0로 입력한다.
x0가 벡터인 경우: f(x0(1))ⅹf(x0(2)) < 0 이 되도록 두 원소는 해의 반대쪽에 있어야 한다. 해가 둘 이상이면, 하나씩 해를 분리해서 구한다.
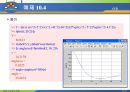
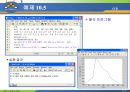
해의 위치의 대략적인 파악을 위해 먼저 함수의 그래프를 그려보는 것이 좋다
fzero 명령어는 함수가 x축과 교차하는 점에서만 함수의 영점(zero)을 구한다. 따라서 함수가 x축에 닿지만 교차하지 않는 점에서는 영점을 구하지 못한다. 해를 구할 수 없으면, NaN을 돌려준다
MATLAB은 광범위한 수학문제들을 수치적으로 풀기 위한 많은 함수 라이브러리를 가지고 있는데, 이 장에서는 이러한 함수들 중에서 가장 빈번하게 사용되는 함수들의 사용방법에 대해 설명한다.
여기서는 MATLAB의 사용방법에 대해 설명하며, 수치해석에 대한 자세한 사항은 수치해석 관련 책을 참조하도록 한다.
이 장에서는 미지수가 한 개인 방정식의 풀이, 함수의 최소값 또는 최대값 구하기, 수치적분, 일차 상미분방정식 등의 주제들을 다룬다.
일변수 방정식 f(x)=0의 해는 함수가 x축과 교차하는(함수 값이 0이 되는) 값, 또는 함수의 부호가 바뀌는 값이다.
정확한 해는 함수의 값이 정확히 0이 되는 x의 값이다. 만일 이러한 값이 존재하지 않거나 구하기 어렵다면, 함수의 부호가 바뀌는, 즉 축과 교차하는 점에 매우 근접한 수치해 x를 구한다. 수치해는 반복과정을 통해 해에 더 가까운 x 값을 구하며, 반복을 해도 더 이상 해가 어떤 한도보다 변하지 않으면 더 이상의 반복을 중지한다.
MATLAB에서 함수의 영점(zero)은 명령어 fzero를 이용하여 구한다:
해를 구할 함수인 입력인자 function의 입력 방법
수학식을 문자열로 입력하는 방법.
ex) x=fzero('x^2-2*x-3', 2)
함수를 함수 파일에서 사용자정의 함수로 만든 다음, 이 함수의 핸들을 입력하는 방법. ex) func.m 파일에 함수가 정의되어 있을 때, x=fzero(@func, 2)
함수를 먼저 익명함수로 정의한 다음, 이 익명함수의 이름을 입력하는 방법.
함수는 표준 형태로 쓴다. 예) 식이 xe-x=0.2 일 때, 'x*exp(-x)-0.2'와 같이 입력.
함수를 문자열로 입력하는 경우, 미리 정의된 변수는 식에 포함될 수 없다.
ex) b=0.2가 정의되어 있을 때, 'x*exp(-x)-b'의 입력은 허용되지 않는다.
x0는 스칼라 또는 두 원소의 벡터가 될 수 있다.
x0가 스칼라인 경우: 함수가 x축과 교차하는 점 근처의 x 값을 x0로 입력한다.
x0가 벡터인 경우: f(x0(1))ⅹf(x0(2)) < 0 이 되도록 두 원소는 해의 반대쪽에 있어야 한다. 해가 둘 이상이면, 하나씩 해를 분리해서 구한다.
해의 위치의 대략적인 파악을 위해 먼저 함수의 그래프를 그려보는 것이 좋다
fzero 명령어는 함수가 x축과 교차하는 점에서만 함수의 영점(zero)을 구한다. 따라서 함수가 x축에 닿지만 교차하지 않는 점에서는 영점을 구하지 못한다. 해를 구할 수 없으면, NaN을 돌려준다
키워드
추천자료
 GIS의 개념 및 개요
GIS의 개념 및 개요 정보시스템 감리의 개요
정보시스템 감리의 개요 지리정보시스템(GIS) 개요
지리정보시스템(GIS) 개요 P2P의 정의, 소리바다 사건의 개요 및 쟁점, 외국 P2P의 현황, 우리나라 소리바다 사용에 대...
P2P의 정의, 소리바다 사건의 개요 및 쟁점, 외국 P2P의 현황, 우리나라 소리바다 사용에 대... 친환경 생태마을 조성 방안, 생태마을 개요, 원리와 유형, 계획기범
친환경 생태마을 조성 방안, 생태마을 개요, 원리와 유형, 계획기범 터치스크린의 정의 및 개요, 동작원리 및 기대효과 및 관련특허, 시장전망
터치스크린의 정의 및 개요, 동작원리 및 기대효과 및 관련특허, 시장전망 지식경영(KM)의 개요와 구조, KM 전략과 전망
지식경영(KM)의 개요와 구조, KM 전략과 전망 e-비즈니스(e-business)의 개요와 구성
e-비즈니스(e-business)의 개요와 구성 모바일 커머스(m-commerce)의 개요, 정의와 관련기술
모바일 커머스(m-commerce)의 개요, 정의와 관련기술 [객체지향프로그래밍][객체지향]객체지향프로그래밍의 개요, 객체지향프로그래밍의 정의, 객...
[객체지향프로그래밍][객체지향]객체지향프로그래밍의 개요, 객체지향프로그래밍의 정의, 객... PLC(프로그램형 제어기)의 개요, PLC(프로그램형 제어기)의 정의, PLC(프로그램형 제어기)의 ...
PLC(프로그램형 제어기)의 개요, PLC(프로그램형 제어기)의 정의, PLC(프로그램형 제어기)의 ... [동작경제원칙] 동작경제원칙의 개요(개념)와 동작경제3원칙(신체부위사용,작업장배치,도구와...
[동작경제원칙] 동작경제원칙의 개요(개념)와 동작경제3원칙(신체부위사용,작업장배치,도구와... [IT] 임베디드 시스템 개요
[IT] 임베디드 시스템 개요 스마트 의류, 소재 조사 자료, 개요, 정보
스마트 의류, 소재 조사 자료, 개요, 정보
















































소개글