토질역학실험-삼축압축실험

소개글

토질역학실험-삼축압축실험에 대한 보고서 자료입니다.

목차

☉개요
☉목적
☉이론적 배경
☉실험방법
☉결과
☉고찰

본문내용

공시체에 따라 다르나 보통 24시간으로 한다.
⑦ 압밀이 완료되면 체적변화량과 압밀침하량을 기록한 다음 모든 밸브를 잠그고 축방향력을 가한다. 압축 속도는 매분 1%의 변형률이 생기도록 한다.
⑧ 압축이 완료되면 파괴 상황을 기록하고 함수비를 측정한다.
결과
○아래 물성치를 이용해 단위중량, 건조단위중량, 포화도, 간극비를 유추해 냈다.
구속압(Kpa)
직경(cm)
높이(cm)
함수비(%)
시료무게(g)
LL(%)
PL(%)
100
5
10
55.2
326.5
44.2
26.6
150
5
10
55
327.5
44.2
26.6
200
5
10
55.4
327.3
44.2
26.6
Gs
2.72
구속압
단위중량(kg/m)
건조단위중량(kg/m)
간극비
포화도
간극률
100
1662.851
1071.425
1.539
0.976
0.606
150
1666.416
1075.107
1.530
0.978
0.605
200
1666.925
1072.667
1.536
0.981
0.606
단위중량 , 건조단위중량
간극비는 을 통해 구할수있다.
또한 포화도는 식을 이용한다.
예를 들어 구속압이 100Kpa일때의 단위중량은 이다.
이때의 건조 단위중량은
간극비 e는 이며 그에따른 포화도 S는
이때의 간극률은 0.606이었다.
○축차응력 는 표에 주어진 axial force를 삼축압축계의 면적으로 나눈 값이다.
따라서 축차응력은 로 나타낼수가 있다.
예를 들어 구속압이 100kpa의 12번째 자료를 통해 축차응력을 구해보겠다.
축력이 20N이고 시료의 지름이 50mm이므로 이에대한 축차응력은 아래와 같이 나타낼수 있다.
○구속압 는 Cell pressure에서 Back pressure(배압)을 뺌으로서 알수 있다.
예를 들어 구속압이 100kpa의 12번째 자료를 통해 구속압을 구해보겠다.
Cell pressure 가 199.9kpa, Back pressure 가 99.9kpa으로 주워져 있으므로, 구속압은 다음과 같이 구할수 있다.
시간에따른 구속압이 정확히 100으로 계속유지는 되지 않지만 그 오차범위가 0.2내외이 므로 100Kpa이라고 정했다.
○구속압과 축차응력을 구했으면 그 둘을 이용해서 최대 응력 을 구할수 있다.
예를 들어 구속압이 100kpa의 12번째 자료를 통해 최대응력을 구해보면 다음과 같다.
kpa
○간극수압()은 가장 처음회 pore press값이 기준이되어 매회에서 처음값 인 100.1kpa을 빼면 얻을수 있다.
예를 들어 구속압이 100kpa의 12번째 자료를 통한 간극수압을 구해보면 다음과 같다.
100.7kpa-100.1kpa=0.6kpa
○간극 수압을 구했으면 과 의 유효응력 을 구할수있다. 이는 전응력에서 간극 수압을 빼면 얻을수 있는 값이다.
구속압이 100kpa의 12번째 자료로 예를 들어보면
○이 자료들을 p,q diagram상에 나타내어 이에 따른 수정파괴포락선과 응력경로를 알기위 해서 p,q ,p',q'값을 구해야 한다. 이 또한 구속압 100kpa에서 12번째 자료를 예를 들면
105.09, 109.59+99.4)=104.49
과 같다.
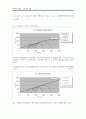
○수정파괴 포락선은 다음과 같다.
시료내의 대표점에서의 응력변화를 나타낸 응력경로를 p-q diagram상에 그려보면 위와 같은 결과를 보여준다. 이 응력경로는 전응력의 결과 즉, 간극수압을 빼지않은 값들의 결과 값이다.
○수정파괴포락선 즉,p-q diagram상에 나타낸 것이 아닌 mohr-Coulomb의 전응력에대한 파괴 포락선은
이는 수정파괴 포락선에서의 점착력(a)과 내부마찰각()으로 다음의 관계를 통해 구했다.
수정 파괴포락선의 값과 mohr-Coulomb의 파괴 포락선의 강도정수중에 mohr-Coulomb의 파괴 포락선을 통한 강도 정수를 사용하기 때문에 파괴포락선의 강도 정수를 구해보았다.
점착력 c=4.9408kpa 이고 내부마찰각 =17.9678이 나왔다.
○수정파괴포락선
앞에서 구한 방법과 같게 계산해보면 이 값들을 쉽게 얻을수 있다.
○파괴포락선
유효응력에 대한 mohr-Coulomb의 파괴 포락선을 통한 강도정수 점착력(c)은 3.0729kpa 이 나왔고 내부마찰각()은 27.0534이다.
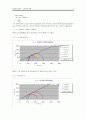
○구속압별 축차응력-변형율 그래프
변형률 은 원래 주어진 축변위 data를 100으로 나눈 백분율 값을 이용하였다.
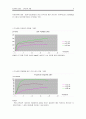
○구속압별 변형률에 따른 간극수압의 변화 그래프
고찰
직접 삼축압축 시험기를 사용해가며 실험을 하지는 않았지만 매우 복잡하고 까다로운 시 험일것이라는 느낌을 데이터를 정리하는 내내 들었다.
우선 CU-test로서 전 응력과 축차응력을 통한 간극수압을 알수 있고 그에 따른 유효응력 도 계산해 낼수 있었다. 수업시간에 교수님께서 중요한 부분이라서 설명을 많이 해주셨는 데 이렇게 데이터를 정리하다보니깐 그때 이해가지 않던 부분이 더욱 이해가 잘되는 것 같 았다. 그래프들로 미루어 봤을때는 선행 압밀을 받지 않은 NC clay류의 흙일꺼 같다는 느 낌을 받았다. 우선 과압밀 점토이면 축차응력-변형률 그래프에서 첨두점을 찍고 내려와야 하는데 여기서 나온 그래프에서는 NC-clay의 특성을 나타내었다. 또한 축차응력으로 인한 간극수압-축변형률 그래프에서도 과압밀 토라면 음의간극수압(부압)이 발생할텐데 구한 그 래프에서는 나타나지 않은 이유에서 정규 압밀 점토라고 미루어 짐작해보았다.
또한 p-q diagram상에 응력경로를 표시하는 과정에서 원래 유효응력에 대한 p‘값은 전응 력에대한 p값에서 간극수압 u를 빼서 계산하는 것 이고 q값은 전응력에 대한 값이나 유효 응력에 대한 값이 같다고 배웠는데 시험결과 역시 그와 같게 나왔다. 유효응력에 대한 응 력경로의 선이 직선이 아닌 구부러진 곡선 형태로 나왔는데 이 이유는 좀더 생각해 보아야 할것같다.
또한 전응력에 대한 파괴포락선의 내부마찰각이 유효응력에 의한 파괴포락선의 내부마찰각 보다 적게나왔다.
이번시험을 통해서 수업시간에 배운 내용들을 완벽하게 숙지할수있는 계기가 되어서 기쁘 다. 한편으로는 중간고사 전에 이 시험을 했더라면 시험공부에 훨씬 도움이 되었을 텐데 라는 아쉬움이 남기도 한다.

키워드

토질역학실험,   삼축압축시험,   레포트,   인하대학교,   토목과