Mass Transfer modeling for Fabrication of titanium-oxide-based solar panels

소개글

Mass Transfer modeling for Fabrication of titanium-oxide-based solar panels에 대한 보고서 자료입니다.

목차

1. Introduction
2. Problem Description & Development
3. Coding & Results
4. Conclusion
5. References

본문내용

e of H₂ Diffused] =
따라서 최종적으로, 을 얻을 수 있다.
에서 , 에서 을 적용하여 적분하면,
→ →
이상으로 필요한 식들을 얻을 수 있었으며, 이제부터는 Matlab Coding을 이용하여 시간에 대하여 가 어떤 식으로 거동하는지 알아보겠다.
3. Coding & Results
1) Matlab을 이용한 Numerical method
코딩은 다음과 같다.
clc
clear all
D=0.01; %D: molecular diffusion coefficient (cm2/s)
C=1.354*10^-5; %C: Solubility of H2 in TiO2(mol H2/cm3)
M=47.9; %M: Molecular weight of Ti(s)(g/mol)
e=2.6; %e: density of Solid nanoporous Ti(s)(g/cm3)
A=(D*C*M/e)*10^8;
%initial condition
y1(1)=0.1; %y1: thickness (μm)
t1(1)=0;
dt=0.001
t1=[0:dt:16];
%numerical method
for n=2:size(t1,2)
y1(n)=A/2*(1/y1(n-1))*dt+y1(n-1);
end
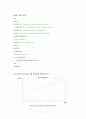
plot(t1,y1)
2) Integration으로 얻은 식을 Matlab을 이용하여 Plot
코딩은 다음과 같다.
clc
clear all
D=0.01; %D: molecular diffusion coefficient (cm2/s)
C=1.354*10^-5; %C: Solubility of H2 in TiO2(mol H2/cm3)
M=47.9; %M: Molecular weight of Ti(s)(g/mol)
e=2.6; %e: density of Solid nanoporous Ti(s)(g/cm3)
t1(1)=0;
dt=0.001;
t1=[0:dt:16];
y1=zeros(length(t1)); %y1: thickness (μm)
y1=(M.*C.*D./e).^0.5*t1.^0.5;
y1=y1*10^4;
% 단위가 cm 이기 때문에 10^4 곱해서 μm 단위로 만들어줌
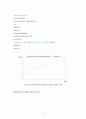
plot(t1,y1)
3) Numerical method로 얻은 데이터와 Integration으로 얻은 데이터의 비교분석
우선, 코딩은 다음과 같다.
clc
clear all
D=0.01; %D: molecular diffusion coefficient (cm2/s)
C=1.354*10^-5; %C: Solubility of H2 in TiO2(mol H2/cm3)
M=47.9; %M: Molecular weight of Ti(s)(g/mol)
e=2.6; %e: density of Solid nanoporous Ti(s)(g/cm3)
A=(D*C*M/e)*10^8;
%initial condition
y1(1)=0.1; %y1: thickness (μm)
t1(1)=0;
dt=0.001
t1=[0:dt:16];
%numerical method
for n=2:size(t1,2)
y1(n)=A/2*(1/y1(n-1))*dt+y1(n-1);
end
plot(t1,y1)
hold on;
y2=zeros(length(t1));
y2=(M.*C.*D./e).^0.5*t1.^0.5;
y2=y2*10^4;
% 단위가 cm 이기 때문에 10^4 곱해서 μm 단위로 만들어줌
plot(t1,y2)
hold on;
육안으로는 잘 구분되지 않는 수준이다.
하지만 그래프를 확대하여 보면 미세한 차이가 있음을 알 수 있다.
이 그래프를 보면, 두 그래프간의 차이점은 존재하는 것을 알 수 있다. 우리는 어느 정도의 오차가 발생하는지 확인하기 위해 Matlab을 이용하여 분석하여 보았다.
코딩은 다음과 같다.
clc
clear all
D=0.01;
C=1.354*10^-5;
M=47.9;
e=2.6;
A=(D*C*M/e)*10^8;
%initial condition
y1(1)=0.1;
t1(1)=0;
dt=0.001
t1=[0:dt:16];
%numerical method
for n=2:size(t1,2)
y1(n)=A/2*(1/y1(n-1))*dt+y1(n-1);
end
y2=zeros(length(t1));
y2=(M.*C.*D./e).^0.5*t1.^0.5;
y2=y2*10^4;
%평균 error 를 계산
error = y1-y2;
average = 0;
for n=1:16001
average = average + error(n);
end
average = average/16001
average = 0.0301
평균 error는 0.0301μm로서 무시할 만한 수준임을 알 수 있었다.
4. Conclusion
Matlab을 이용하여 태양전지 판 Titanium가공 공정에서 시간에 따른 두께 변화를 그래프 화 할 수 있었다. 두께 증가 속도는 시간이 흐름에 따라 감소함을 알 수 있었다. 또한 Numerical method로 얻은 데이터와 Integration을 통해 얻은 데이터를 비교함으로써 Numerical method의 신뢰성을 확인할 수 있었고, Mass-transfer에서 사용되는 다른 여러 가지 미분방정식에 Numerical method를 충분히 적용할 수 있음을 확인했다.
졸업 후 여러 가지 기업과 현장에 진출하게 된다면 화학공학을 전공한 Engineer로서, Mass-transfer 지식을 활용하여 다양한 분야의 공정에서 필요한 데이터들을 계산하고 예측하는 것이 요구될 것이다. 이번 프로젝트를 통해 Matlab을 활용하여 복잡한 미분방정식을 컴퓨터를 이용하여 처리하는 방법을 습득할 수 있었다. 사회에 기여하는 화학공학 엔지니어가 될 수 있도록 전공지식 활용능력을 더욱 기를 수 있도록 노력해야할 것이다.
5. References
§ 박남규, '연료감응태양전지' Polymer Science & Technology Vol.17, No.4, August 2006
§ Welty, Wicks, Wilson, Rorrer, "Fundamentals of Momentum, Heat, and Mass
Transfer" 5th Edition

키워드

Matlab,   Numerical method,   Integration,   물질이동론 프로젝트