자동제어 크레인 설계보고서

소개글

자동제어 크레인 설계보고서에 대한 보고서 자료입니다.

목차

Ⅰ. 설계 목표
1. 설계배경

Ⅱ. 설계
1. 설계조건
1) 입력 2개, 출력2개 MIMO System 구축
2) 상태방정식을 이용하여 PID 제어기 설계
3) MATLAB Simulink를 이용한 Simulation 실시
2. 모델링
1) 제어대상
2) 운동방정식
3) 상태방정식

Ⅲ. Simulation by MATLAB
1. M-File 작성
2. 제어시스템 구축
3. PID제어기 설계

Ⅳ. 설계 결과 분석 및 안정성 평가

Ⅳ. 참고 문헌

본문내용

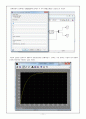
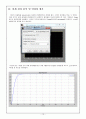
력한 각 각의 행렬을 Matrix Gain으로 주었다.
이상의 값들을 입력하고 500초의 Simulation을 실행하였고, 결과로 나온 출력은 다음과 같이 300초 근처에 안정하게 수렴하는 값을 가졌다.
3. PID제어기 설계
위와 같은 System에서는 단위입력을 주었을 때 안정한 값을 얻기까지 너무도 긴 시간이 걸린다. 이와 같은 System에서 기준입력에 대한 빠른 플랜트출력을 얻도록 하기 위해서 PID제어기를 설계한다. 제어기의 설계에 앞서 먼저 PID제어기의 특징을 살펴보면 다음과 같다.
□ 비례(P) 제어 (Proportional control)
ㆍ 제어신호를 오차신호(기준입력과 출력의 차이)를 증폭하여 얻음
ㆍ 정상상태오차를 감소시킬 수 있음
ㆍ 하지만, 정상상태오차를 완벽히 제거할 수는 없음
□ 적분(I) 제어 (Integral contrl)
ㆍ 제어신호를 오차신호로 적분하여 얻음
ㆍ 정상상태오차를 완벽히 제거할 수 있음
ㆍ 하지만, 과도응답이 악화되는 경향이 있음
□ 미분(D) 제어 (Derivative control)
ㆍ 제어신호를 오차신호로 미분하여 얻음
ㆍ 과도응답을 향상시킬수 있음
□ PID제어기의 형태
여기서, e(t) = r(t) - y(t)
r(t) : 기준입력, y(t) : 플랜트 출력
□ 전달함수
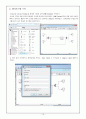
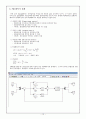
MATLAB Simulink Library를 통해 다음과 같은 PID제어기를 설계한다. 도서와 인터넷 실험실을 방문하여 문의하였다. 출력물은 부록에 첨부하도록 한다.
초기에 비례기의 Gain을 1로 하고, 적분기와 미분기의 Gain을 0으로 두었을때, 처음과 같은 출력을 얻을 수 있었다.
더욱더 안정화되고 빠른시간에 정착시간에 도달하는 시스템을 구축하기 위해서 PID제어기에 실험적으로 임의의 Gain값을 넣어가면서 반복하여 튜닝 하였고, 2가지의 안정화된 System을 얻을 수 있었다.
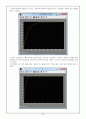
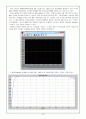
첫 번째로 나온 것은 P값을 250, I값을 0.01, D값을 0으로 두었을 때, 다음과 같은 출력을 얻을 수 있었다.
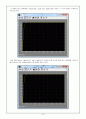
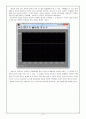
두 번째로 얻은 출력에서는 P값을 550, I값을 0.05, D값을 20을 주었다. 각 각의 출력은 부록에 첨부하도록 한다.
입력 값이 Km1*v1, Km2*v2이고, Km1 = Km2이므로 동일한 전압 v(t)에 대해 같은 출력값을 가지므로 출력 y2또한 다음 그림에서처럼 y1과 동일한 값이 나온다.
Ⅳ. 설계 결과 분석 및 안정성 평가
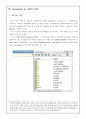
이상으로 MATLAB simulation을 통해서 PID제어기를 설계해 봤고, 2개의 결과물을 얻을 수 있었다. 이제 초기의 설계 출력값과 PID제어기의 설계후의 출력값을 비교분석해보도록 하자. 위에서는 Scope창으로 출력결과를 살펴봤다. 하지만 보기에 불편함으로 Scope데이터를 workspace에 저장하고, plot를 실행시켜서 결과를 분석 해보았다.
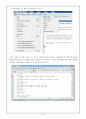
다음과 같은 그림을 얻기 위해 plot(Report1y1.time, Report1y1.signals.values)를 띄우고, grid on하고, 타이틀 및 폰트를 수정하였다.
위의 그래프는 PID제어기에서 P값을 250, I값을 0.01, D값을 0으로 주었을때의 출력이다. 우선 초기의 300초가량에서 정착화되던 시스템이 PID제어기에 의해 0.9초가량에 정착화 되는 것을 볼 수 있다.
이러한 출력을 얻기 위해서 비례기의 값을 250정도로 주었다. 비례기의 값을 크게 하면 할수록 더욱더 빠른 시간에 목표치에 도달할 수 있지만, 값이 과도하게 커지게 될 경우, 과도응답에서 오버슛이 발생하게 된다. 비례값을 높여서 더욱 빠른 정착시간을 얻을 수도 있지만, 더욱 더 많은 에너지를 필요하게 되고, 이 값을 250으로 두었을 때에는 오버슛이 발생하지 않아서 미분기의 값을 0으로 둘 수 있었고 이 설계에서는 굳이 PID제어기를 설계하지 않더라도 PI제어기 만으로도 충분히 안정화된 System을 구축할 수 있고 자원도 절약할 수 있다. 안정성의 평가를 위해서 기준으로 오차범위 기준을 ± 0.1%로 잡았고 적분기값을 0.01로 주었을 때 다음과 같이 오차율은 0.005%로 상당히 안정된 결과를 나타내었다.
두 번째 System의 설계에서는 P값을 550, I값을 0.05, D값을 20을 주었다. 결과는 다음과 같다.
전자의 결과 보다 후자의 결과가 더욱 더 좋은 System이라 할 수 있다. 비례값을 더 높은 값인 550으로 주었기 때문에 보는바와 같이 0.5초에서 정착되는 것을 볼 수 있다. 하지만, 비례값이 높아짐에 따라 오버슛이 생기는 등 과도특성이 나쁘게 나타났다. 이러한 과도응답을 향상시키기 위해서 미분기의 값을 20으로 주었을때, 오버슛은 사라지고 과도응답이 개선되었다. 마찬가지로 안정성 평가를 실시하기 위해서 동일한 오차범위 ± 0.1%로하고, 미분기 값을 0.05로 두었을 때 오차율은 0.001%로 매우 안정된 형태로 나왔다.
이상으로 트랜스퍼 크레인의 주행제어를 위한 2가지의 PID출력을 비교해 보았다. 두 결과값 모두 상당히 좋은 결과로 평가 할 수 있다. 두 결과를 비교해 봄으로써 어떠한 상황에서 사용하는가에 따라 각기 다른 값으로 설계를 할 수 있다는 것을 알게 되었다. 전자의 경우는 후자의 경우보다 약간의 오차가 더 있고 0.4초정도 더 늦게 정착하지만 에너지 절약적 측면에서 본다면 후자의 경우보다 낮다. 반면에 후자의 경우는 에너지가 조금 더 들더라도 정확도를 필요로하는 곳에 사용되기에 적합해 보인다.
Ⅴ. 참고 문헌
1. 2학년 과제 프린트
2. 김영복, 서진호, 이권순 “트랜스퍼 크레인의 모델링 및 고정도 주행제어기 설계에 관한 연구”
3. 김영복, 정황훈, 양주호 “트랜스퍼 크레인의 이송위치제어를 위한 서보계 설계 : 가중H 오차사양을 만족하는 동일차원 관측기 설계”
4. MATLAB 입문과 활용 김용수 저 출판사 : 높이깊이
5. 공학도를 위한 매트랩7 김우식 박민기 박익근 공역 출판사 : 교보문고
6. 기초부터 응용까지 MATLAB 프로그래밍 응용 여영구 역 출판사 : 아진
7. 이공계 과학도를 위한 MATLAB 사용법과 그 응용 김창근 지음
8. 프로젝트식으로 배우는 MAT/Simulink의 기초 박전수 역 출판사 : 아진

키워드

자동제어,   크레인 설계보고서,   설계결과,   제어시스템,   모델링