행정계량분석 ) 1무작위 표본 추출의 다섯 가지 방법 2

소개글

행정계량분석 ) 1무작위 표본 추출의 다섯 가지 방법 2에 대한 보고서 자료입니다.

목차

행정계량분석
다음을 간단히 설명하시오 (그림 및 수식을 활용)
1.무작위 표본 추출의 다섯 가지 방법
2.산술 평균의 개념 및 특성
3.분산과 표준편차의 개념 및 계산식
4.정규분포의 네 가지 특징
5.중심극한정리

목차

1. 무작위 표본 추출의 다섯 가지 방법
1) 복권 추첨 방식에 의한 표본 추출
2) 난수표에 의한 표본 추출
3) 체계적 표본추출(Systematic Sampling)
4) 층화표본추출(Stratified Sampling)
5) 군집표본추출(Cluster Sampling)
2. 산술 평균의 개념 및 특성
1) 산술 평균의 개념
2) 산술 평균의 특성
3. 분산과 표준편차의 개념 및 계산식
1) 분산과 표준편차의 개념
2) 분산과 표준편차의 계산식
4. 정규분포의 네 가지 특징
1) 평균()과 표준편차()가 정규분포의 모양과 위치를 결정한다.
2) 정규분포는 평균()을 중심으로 대칭인 종모양이다.
3) 정규분포는 -∞< X < +∞의 범위에서 X값을 갖는다.
4) 정규분포 곡선과 X축 사이의 면적은 1이다.
5. 중심극한정리
6. 출처 및 참고문헌

본문내용

수로 나누어 산술 평균을 구하기 때문에 나타나는 특성이다. 예를 들어 [1, 2, 3, 99]로 구성된 모집단의 평균의 값은 26.25로, 극단 값인 99를 제외했을 때의 평균인 2와는 큰 차이가 난다. 두 번째로 산술 평균의 편차의 합은 0이다. 세 번째로 분산의 크기가 가장 작게 나타난다. 마지막으로 다른 평균에 비해서 표본의 평균과 모집단의 평균의 차이가 크게 나타나지 않는다.
3. 분산과 표준편차의 개념 및 계산식
1) 분산과 표준편차의 개념
분포의 분산도를 표현할 때 분산과 표준편차가 가장 많이 사용된다. 분산이란 표본 내의 변수들이 흩어져있는 정도를 계산하는 지표로써, 각 변량이 평균에서 어느 정도 벗어나 있는지를 나타내는 지표라고 이해하면 된다. 모집단을 대상으로 분산을 표현할 때에는 보통 기호를, 표본을 대상으로 분산을 표현할 때에는 보통 기호를 사용한다.
표준 편차는 산포도(Dispersion) 중 하나이다. 여기서 산포도란 변량이 분포의 중심 값에서 흩어져 있는 정도를 말한다. 앞서 설명했듯이, 가장 빈번하게 사용되는 평균값이 산술 평균이고, 가장 빈번하게 사용되는 산포도가 표준편차이다. 표준 편차는 자료의 변량이 흩어져 있는 정도를 나타내는 값을 말한다. 모집단을 대상으로 표준편차를 표현할 때에는 보통 기호를, 표본을 대상으로 표시할 때 보통 기호를 사용한다.
보통 분산과 표준편차는 함께 언급되는데, 제곱 단위의 분산을 실제 관찰되는 값과 같은 크기로 바꾸기 위해 제곱근을 씌운 값이 표준편차이기 때문이다.
2) 분산과 표준편차의 계산식
모집단의 분산
모집단의 표준편차
표본의 분산
표본의 표준편차
표2. 분산과 표준편차의 계산식
분산은 각각의 관찰 값에 대한 평균과의 편차 값을 제곱한 후, 그 평균을 구한 것이다. 관찰 값과 평균과의 편차 값이 음(-)의 수치를 띌 수 있기 때문에 제곱하여 평균을 구한다. 그런데, 분산은 편차의 값을 제곱하여 구한 값이기 때문에 관찰 값을 그대로 반영하기 어렵다는 문제를 안고 있다. 표준편차는 이러한 문제를 해결하기 위해 분산 값에 제곱근을 씌운다. 이를 통해 관찰 값과의 유사성을 확보한다.
모집단의 분산과 표준편차를 구할 때 N(모집단을 구성하는 관찰 값의 개수)개로 나누는 데에 반하여 표본의 분산과 표준편차를 구할 때는 n-1으로 나누어 준다. 이는 모집단의 를 추정하기에 적합한 불편추정량(Unbiased Estimator)을 만들기 위함이다. 여기서의 추정량은 모집단의 모수를 추정하기 위해 추출한 표본들을 말한다. 불편추정량은 이러한 추정량의 기대값과 모수가 일치했을 때의 추정량을 말한다. 쉽게 말해서 불편추정량은 모집단의 모수와 일치하게 만드는 추정량이라고 할 수 있다.
4.정규분포의 네 가지 특징
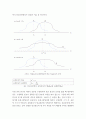
정규곡선으로부터 유래된 정규분포는 연속 확률 분포 중에서 가장 많이 활용되는 분포이다. 아래의 그래프1은 평균()과 표준편차()에 따른 정규분포의 모양을 보여준다. 그래프1을 통해서 알 수 있는 정규분포의 네 가지 특징은 다음과 같다.
1) 평균()과 표준편차()가 정규분포의 모양과 위치를 결정한다.
그래프를 통해 볼 수 있듯이, 정규분포의 평균과 표준편차가 정규분포의 모양과 위치를 결정한다. 표준편차가 동일할 경우 정규분포의 모양이 동일하고, 평균이 같을 경우에는 정규분포의 중심점이 동일하다. 그렇기 때문에 그래프에 나타난 것과 같이 다양한 모양의 정규분포가 존재할 수 있다.
2) 정규분포는 평균()을 중심으로 대칭인 종모양이다.
그래프를 통해 볼 수 있듯이, 정규분포는 평균()을 중심으로 좌우 대칭을 이루는 종 모양 형태로 그려진다. 평균에 가까운 곳에 확률 값이 많이 존재하고, 평균에서 먼 곳일수록 확률 값이 적게 존재한다. 평균()과 표준편차()의 수치에 좌우되지 않으며 정규분포는 항상 종 모양을 이룬다.
3) 정규분포는 -∞< X < +∞의 범위에서 X값을 갖는다.
그래프를 통해 볼 수 있듯이, 정규분포의 곡선은 X축에 맞닿지 않는다. 그렇기 때문에 최댓값과 최솟값이 존재하지 않아 정규분포는 항상 -∞< X < +∞의 범위에서 X값을 갖게 된다. 정규분포가 무한대(∞)의 영역을 다룬다는 점은 정규분포가 세상에 존재하는 모든 현상 연구를 다룰 수 있다는 점을 시사한다.
4) 정규분포 곡선과 X축 사이의 면적은 1이다.
분포의 평균()과 표준편차()의 값과 무관하게 정규곡선과 X축 사이의 면적은 언제나 1이다.
5. 중심극한정리
앞서서 정규분포가 연속 확률 분포 중에서 가장 많이 활용되는 분포라고 설명했다. 실제로 정규분포가 널리 사용되는 이유는 중심극한정리가 성립하기 때문이기도 하다.
중심극한정리는 평균이 , 분산이 인 모집단에서 크기가 n인 모든 표본을 추출했을 때, 모집단의 분포 형태와는 무관하게 평균의 표집분포가 평균의 크기인 n을 증가시킬수록 정규분포에 가까워진다는 이론이다. 중심극한정리는 통계학에서 가장 중요한 정리라고 해도 과언이 아니다. 모집단의 분포 모양과는 무관하게 표본의 크기를 증가시킬수록 정규분포에 가까워져, 정규분포의 성질을 이용할 수 있게 하기 때문이다. 중심극한정리는 모집단 변수의 분포가 어떠한가에 좌우되지 않는다는 점 역시 중심극한정리가 중요한 이유 중 하나이다.
표집분포의 평균
표집분포의 표준편차
표4. 중심극한정리 표집분포의 평균()과 표준편차()
사회 과학 연구를 하면서 표본을 수량화하여 표본 분포의 모양을 봤을 때 대부분의 경우, 수량화된 분포가 정확한 정규 분포의 모양을 띠지 않는다. 그런데 사회 과학 연구를 할 때 불가피한 경우를 제외하고, 비교적 큰 표본을 뽑는 경우가 많다. 그렇기에 중심극한정리가 중요하다. 중심극한정리에 따라서 모집단의 크기 즉, 표본의 크기가 커질수록 표집분포가 정규분포에 가까워지기 때문이다. 정규분포에 가까워진 분포는 앞서 설명한 정규분포의 네 가지 특징을 띄기 때문에 수치를 계량화하고 특정한 기준과 결과를 추출하기 용이해진다. 즉, 중심극한정리는 수집한 통계량을 이용하여 모집단의 특이점을 추정해낼 수 있는 수학적인 근거를 제공해준다.
6. 출처 및 참고문헌
박정식, 윤영선, 박래수, 「제5판 현대통계학」, 다산출판사, 2016

키워드

과제,   레포트,   논문,   사이버,   학점은행,   일반대학,   오프라인,   온라인,   일지