목차
1. 실험목적
2. 관련 이론
1) 벤추리 메타
(2) 급 확대관(sudden expension)
(3) 오리피스 (orifice)
(4) Elbow
3. 참고 문헌
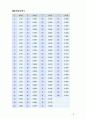
1)유량단위 환산표
2)물의점성계수
2. 관련 이론
1) 벤추리 메타
(2) 급 확대관(sudden expension)
(3) 오리피스 (orifice)
(4) Elbow
3. 참고 문헌
1)유량단위 환산표
2)물의점성계수
본문내용
되는 단면을 가진 관으로 축소부분에서 정력학적 수두의 일부는 속 도수두로 변하게 되어 관의 목 부분의 정력학적 수두보다 적게 되는데 이러한 수두의 차에 의해 직접적으로 유량을 계산할 수 있다. 오리피스에 비해 압력 손실이 적으나 값이 상대적으로 비싸고 유량변화에 따라 목 직경을 변화시킬 수 없다.
그림에서 1, 2점의 유동유체가 비압축성 유체일 경우 Bernoulli\'s 방정식에서
연속방정식에서
(m/s)
(㎡/s)
따라서, 벤츄리의 유량은
(㎡/s)
여기에서
: 벤츄리의 실제유량(m3/s) : 이론유량(m3/s) : 평균속도(m/s)
: 최대 직경(m) : 최소 직경(m) :: 물의 비중
: 마노메터 차압(m) : 유량계수(=0.98)
(2) 급 확대관(sudden expension)
급 확대관
유로의 물이 작은 지름에서 갑자기 큰 지름의 관으로 유동할 때 와류와 박리 로 인하여 큰 에너지 손실이 발생한다.
Bernoulli\'s 방정식과 연속방정식에 의해
여기에서
: 에서의 평균유속(m/s) : 에서 평균유속(m/s)
(3) 오리피스 (orifice)
그림2. orifice
- 유량측정계인 오리피스로서 압력 차를 측정하여 이론 유량을 구하고 실제 의 유량과 비교하여 오리피스 유량계수를 구한다.
- 오리피스는 설치에 비용이 적게 들고 비교적 유량측정이 정확하여 얇은 판 오리피스가 널리 이용되고 있으며 흐름의 수로 내에 설치한다. 오리피 스를 사용하는 방법은 노즐과 벤츄리 미터와 같다.
- 오리피스의 장점은 단면이 축소되는 목부분을 조절함으로써 유량이 조절 된다는 점이며, 단점은 오리피스 단면에서 커다란 수두손실이 일어난다는 점이다.
그림에서 1, 2 점의 유동유체가 비압축성 유체일 경우 베르누이 방정식에서
연속방정식에서
따라서 오리피스의 유량은
여기에서
: 벤츄리의 실제 유량 : 이론 유량 V : 평균 속도
: 최대 직경(m) : 최소 직경(m) : 물의 비중
: 마노메터 차암(m) : 유량 계수(=0.98)
(4) Elbow
구부러진 관에서의 유동은 벽면에서의 유동박리현상, 2차 유동 등으로 인하여 에너지 손실이 발생한다.
H : 손실수두(m) K : 손실계수 V : 평균속도(m/s)
Δh : 손실측정 수두(m)
엘보일 경우 K = 0.3~ 0.5 , 90 곡관일 경우 K = 0.2~ 0.3
3. 참고 문헌
기초기계공학실험 수업교재
인터넷 백과사전
1)유량단위 환산표
2)물의점성계수
그림에서 1, 2점의 유동유체가 비압축성 유체일 경우 Bernoulli\'s 방정식에서
연속방정식에서
(m/s)
(㎡/s)
따라서, 벤츄리의 유량은
(㎡/s)
여기에서
: 벤츄리의 실제유량(m3/s) : 이론유량(m3/s) : 평균속도(m/s)
: 최대 직경(m) : 최소 직경(m) :: 물의 비중
: 마노메터 차압(m) : 유량계수(=0.98)
(2) 급 확대관(sudden expension)
급 확대관
유로의 물이 작은 지름에서 갑자기 큰 지름의 관으로 유동할 때 와류와 박리 로 인하여 큰 에너지 손실이 발생한다.
Bernoulli\'s 방정식과 연속방정식에 의해
여기에서
: 에서의 평균유속(m/s) : 에서 평균유속(m/s)
(3) 오리피스 (orifice)
그림2. orifice
- 유량측정계인 오리피스로서 압력 차를 측정하여 이론 유량을 구하고 실제 의 유량과 비교하여 오리피스 유량계수를 구한다.
- 오리피스는 설치에 비용이 적게 들고 비교적 유량측정이 정확하여 얇은 판 오리피스가 널리 이용되고 있으며 흐름의 수로 내에 설치한다. 오리피 스를 사용하는 방법은 노즐과 벤츄리 미터와 같다.
- 오리피스의 장점은 단면이 축소되는 목부분을 조절함으로써 유량이 조절 된다는 점이며, 단점은 오리피스 단면에서 커다란 수두손실이 일어난다는 점이다.
그림에서 1, 2 점의 유동유체가 비압축성 유체일 경우 베르누이 방정식에서
연속방정식에서
따라서 오리피스의 유량은
여기에서
: 벤츄리의 실제 유량 : 이론 유량 V : 평균 속도
: 최대 직경(m) : 최소 직경(m) : 물의 비중
: 마노메터 차암(m) : 유량 계수(=0.98)
(4) Elbow
구부러진 관에서의 유동은 벽면에서의 유동박리현상, 2차 유동 등으로 인하여 에너지 손실이 발생한다.
H : 손실수두(m) K : 손실계수 V : 평균속도(m/s)
Δh : 손실측정 수두(m)
엘보일 경우 K = 0.3~ 0.5 , 90 곡관일 경우 K = 0.2~ 0.3
3. 참고 문헌
기초기계공학실험 수업교재
인터넷 백과사전
1)유량단위 환산표
2)물의점성계수


























소개글