2023년 1학기 방송통신대 신뢰성공학 중간과제물)2번, 3번, 4번 문제(어느 아이템 50개에 대한 수명시험 결과 다음과 같은 데이터를 얻었다 병렬계, 리던던트 시스템, 대기 리던던트 시스템의 현실적인 예 캐플런-마이어 추정법 등)

소개글

2023년 1학기 방송통신대 신뢰성공학 중간과제물)2번, 3번, 4번 문제(어느 아이템 50개에 대한 수명시험 결과 다음과 같은 데이터를 얻었다 병렬계, 리던던트 시스템, 대기 리던던트 시스템의 현실적인 예 캐플런-마이어 추정법 등)에 대한 보고서 자료입니다.

목차

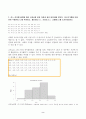
2. 어느 아이템 50개에 대한 수명시험 결과 다음과 같은 데이터를 얻었다. 히스토그램을 이용하여 수명분포를 추정하고, 불신뢰도, 신뢰도, 고장률를 도시하라(5점).

3. 병렬계, 리던던트 시스템, 대기 리던던트 시스템의 현실적인 예를 들어라. (5점)

①병렬계
②m/n 리던던트 시스템
③대기 리던던트 시스템

4. =5개의 어느 부품에 대한 수명실험에 의하여 다음과 같은 데이터가 얻어졌다.
15.4, 5.5, 10.8+, 20.6, 18.9+ (+ 표시는 중도중단시간을 나타냄)

4.1 캐플런-마이어 추정법에 의해 를 구하고, 이의 95% 신뢰구간도 구하라. (5점)
4.2 R을 이용하여 시간 t에 따른 신뢰도의 추이와 95% 신뢰구간을 그려라. (5점)

5. 참고문헌

본문내용

스템은 브레이크 패드, 브레이크 디스크, 브레이크 플루이드, 브레이크 캘리퍼 등 여러 부품으로 이루어져 있다. 이때, 일부 부품이 고장이 나더라도 충분한 수의 부품이 올바르게 동작하면 전체 시스템은 여전히 정상적으로 작동하므로, 자동차의 브레이크 제동 시스템은 m/n 리던던트 시스템의 예가 될 수 있다.
또한 대부분의 대형 항공기는 두 개 이상의 엔진을 가지고 있는데, 두 개 이상의 엔진 중 적어도 하나 이상이 작동해야 항공기가 안전하게 비행 가능하므로 m/n 리던던트 시스템의 예라고 할 수 있다.
③대기 리던던트 시스템
대기 리던던트 시스템[standby redundant system 또는 passive parallel system(수동 병렬계)]은 하나의 구성품(주부품)만 사용상태에 두고 나머지는 필요할 때까지 대기상태로 두는 시스템이다. 따라서 대기 리던던트 시스템의 수명은 주부품 1개만 있는 시스템의 수명보다 더 길다. 일상에서 쉽게 관찰할 수 있는 대기 리던던트 시스템의 예로는 가정용 발전기가 있다. 가정용 발전기는 일상 생활에서 정전이 발생했을 때 사용되는데, 이때 대기 리던던트 시스템으로 작동한다. 발전기는 일반적으로 전원 공급이 원활하지 않은 상황에서만 사용되므로, 그 외의 경우에는 대기 상태로 남겨둔다. 그리고 전기가 필요한 상황에서 발전기를 즉시 사용할 수 있다. 따라서, 가정용 발전기는 대기 리던던트 시스템의 예시 중 하나로 볼 수 있다.
4. =5개의 어느 부품에 대한 수명실험에 의하여 다음과 같은 데이터가 얻어졌다.
15.4, 5.5, 10.8+, 20.6, 18.9+ (+ 표시는 중도중단시간을 나타냄)
4.1 캐플런-마이어 추정법에 의해 를 구하고, 이의 95% 신뢰구간도 구하라. (5점)
캐플런-마이어 추정법의 순서(p67)라 중도중단시간을 포함한 관측값을 작은 것부터 큰 것으로 순차적으로 나열한 후, (5.5, 1),(10.8, 0),(15.4, 1),(18.9, 0),(20.6, 1)의 5개 관측값을 얻게 되고, 신뢰도 로 계산한다.
0≤<5.5 일 때,
5.5≤<15.4 일 때,
15.4≤<20.6 일 때,
≥20.6 일 때,
따라서 = 0.533이다.
의 표준편차 추정치는 교재 p68의 식 (4.6)에 따라 다음과 같다.
따라서 의 95% 신뢰구간은 교재 p68의 식 (4.8)에 따라 다음과 같다.
이 된다.
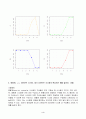
4.2 R을 이용하여 시간 t에 따른 신뢰도의 추이와 95% 신뢰구간을 그려라. (5점)
t = c(5.5, 10.8, 15.4, 18.9, 20.6)
d = c(1, 0, 1, 0, 1)
rel.data = data.frame(t, d)
library(survival)
rel <- survfit(Surv(t, d) ~ 1, type=\"kaplan-meier\", conf.type=\"plain\", data=rel.data)
summary(rel)
plot(rel, xlab=\"time\", ylab=\"reliability\")
5. 참고문헌
신뢰성공학, 백재욱·박정원 공저 2023년

키워드

방송통신대신뢰성공학,   방송대신뢰성공학,   방통대신뢰성공학