2023년 2학기 방송통신대 대학수학의이해 중간과제물)자신의 실제 CAS 사용 경험이나 학습 경험을 명시적으로 기술 CAS 등 컴퓨터 소프트웨어를 이용한 수학 학습 방법에 대해 찬성 또는 반대 실수 구간 S가 있다고 할 때 등

소개글

2023년 2학기 방송통신대 대학수학의이해 중간과제물)자신의 실제 CAS 사용 경험이나 학습 경험을 명시적으로 기술 CAS 등 컴퓨터 소프트웨어를 이용한 수학 학습 방법에 대해 찬성 또는 반대 실수 구간 S가 있다고 할 때 등에 대한 보고서 자료입니다.

목차

1. 1970년대 초부터 개발되기 시작한 CAS(Computer Algebra Systems)는 수학 연산을 쉽게 접근할 수 있게 하고 연산 시간을 줄여주어 유사한 문제를 반복적으로 학습할 수 있도록 도울 수 있다는 장점이 있다. 반면, CAS에 지나치게 의존하면 수학적 개념을 놓치고 수학의 본질적 논리 체계를 제대로 학습할 수 없다는 우려도 있다.
① 자신의 실제 CAS 사용 경험이나 학습 경험을 명시적으로 기술하고 (ex. O월 O일 O시 대학수학의 이해 교과목 동영상 강의 수강 후 학습 중 Maxima 실습) ② CAS 등 컴퓨터 소프트웨어를 이용한 수학 학습 방법에 대해 찬성 또는 반대 중 하나의 입장을 택하여 자신의 견해를 독창적으로 논하시오. (총 9점)

2. 실수 구간 S가 있다고 할 때 그 구간에 속한 실수에 관해 다음 물음에 답하시오. (총 8점)
1) 상계, 하계, 최소 상계, 최대 하계의 정의를 기술하시오. (4점)
2) 상계만 존재하고 하계, 최댓값, 최솟값은 존재하지 않는 구간의 예를 들어보시오. (2점)
3) 하계와 최솟값은 존재하나 상계와 최댓값은 존재하지 않는 구간의 예를 들어보시오. (2점)

3. 교재의 <정리 3.5>는 수열 {}의 무한급수가 수렴하면 →0임을 나타내고 있다. ① 이 명제의 역, 즉 “→0이면 수열 {}의 무한급수가 수렴한다.”는 참인지 거짓인지 밝히고, ② 참이면 증명을 하고, 거짓이면 반례를 드시오. (총 5점)
1) <정리 3.5>의 역이 참인지 거짓인지 증명
2) 반례들 ①반례1 ②반례2

4. 다음 문제의 풀이과정과 답안을 상세하게 제시하시오. (총 8점)
1) 을 구하시오. (4점)
2) 의 값을 구하기 위해 적절한 그래프의 개형을 그리고 이를 통해 답안을 유추하시오. (4점)

5. 참고문헌

본문내용

있다. 학습은 눈으로만 하는 것이 아니다. 그렇다고 머리로 생각하는 것이 학습의 전부가 아니다. 학습은 오감과 온몸을 사용하는 보다 적극적인 행위다. 여기서 CAS도 하나의 수단일 뿐이다. 그리고 직접 손으로 풀어봐야 체득되고 나아가 다양하고 복잡한 문제에 응용하며 본질적인 이해에 가까워지는 과정에서 실력과 자신감이 생긴다. 스티븐 호킹 같은 천재가 아닌 이상 학습은 풀이 과정 속에서 시행착오를 통해 이루어진다. 앞에서도 언급했듯이 탁월한 계산력의 인공지능도 그 알고리즘을 보면 시행착오의 반복 과정이다.
정답을 바로 보여주는 공식을 알 수 없는 이상, 시행착오 외에 정답을 알 수 있는 방법은 존재하지 않다고 보는 것이 현실적이다. 결론적으로 말하면 CAS 등의 소프트웨어는 수학 개념을 이해하거나 데이터의 특징을 파악하는 수단으로 활용해야 한다. 만약 소프트웨어로 계산한 정답에만 매몰되면 수학의 기초 개념을 이해하지 못하고 나아가 실질적인 문제 해결 능력을 키울 수 없게 될 것이다.
2. 실수 구간 S가 있다고 할 때 그 구간에 속한 실수에 관해 다음 물음에 답하시오. (총 8점)
1) 상계, 하계, 최소 상계, 최대 하계의 정의를 기술하시오. (4점)
실수 구간 S가 있으며 그 구간 S에 속한 모든 실수 x에 대해 x≤a인 실수 a가 있다고 하자. 이때 a보다 크거나 같은 실수를 구간 S의 상계(upper bound)라고 하고, 구간 S는 a에 의해 위로 유계되었다고 한다. 만약 a가 구간 S에 속하면 a는 구간 S의 최대값이라고 하고, 그 구간의 상계가 없다면 이는 위로 유계되지 않았다고 한다.
실수 구간 S가 있으며 그 구간 S에 속한 모든 실수 x에 대해 x≥b인 실수 b가 있다고 하자. 이때 b보다 작거나 같은 실수를 구간 S의 하계(lower bound)라고 하고, 구간 S는 b에 의해 아래로 유계되었다고 한다. 만약 b가 구간 S에 속하면 b는 구간 S의 최솟값이라고 하고, 그 구간의 하계가 없다면 이는 아래로 유계되지 않았다고 한다.
상계나 하계는 일반적으로 유일하게 결정되지 않는다. 어떤 구간 S의 최소 상계(least upper bound)는 모든 상계 중에서 최소인 수이다. 구간 S의 최대 하계(greast lower bound)는 모든 하계 중에서 최대인 수이다. 최소 상계, 최대 하계가 존재하면 그것은 유일하게 결정된다.
2) 상계만 존재하고 하계, 최댓값, 최솟값은 존재하지 않는 구간의 예를 들어보시오. (2점)
S = (∞,1)
이 구간은 1보다 작은 모든 실수를 나타내지만 1 자체는 포함하지 않는다. 또한 이 구간은 왼쪽으로 음의 무한대 방향으로 무한히 확장된다. 따라서 이 구간에서는 상계 1만 존재하고 하계, 최댓값, 최솟값은 존재하지 않는다.
3) 하계와 최솟값은 존재하나 상계와 최댓값은 존재하지 않는 구간의 예를 들어보시오. (2점)
S = [1,∞)
이 구간은 1 이상의 모든 실수를 나타낸다. 이 구간은 1에서 시작하여 양의 방향으로 무한히 확장된다. 따라서 이 구간에서는 1은 하한과 최솟값에 해당하지만, 상계와 최댓값은 존재하지 않는다.
3. 교재의 <정리 3.5>는 수열 {}의 무한급수가 수렴하면 →0임을 나타내고 있다. ① 이 명제의 역, 즉 “→0이면 수열 {}의 무한급수가 수렴한다.”는 참인지 거짓인지 밝히고, ② 참이면 증명을 하고, 거짓이면 반례를 드시오. (총 5점)
1) <정리 3.5>의 역이 참인지 거짓인지 증명
조건명제 p→q가 참이면, 그 명제의 대우 ~q→~p도 참이 된다.
그러나 그 명제의 역 q→p도 참인 것은 아니다.
따라서 <정리 3.5>에 의해 수열 {}의 무한급수가 수렴하면 →0이 참이므로, →0이 아니면 무한급수는 발산한다는 대우는 참이 된다.
반면 <정리 3.5>의 역, 즉 →0이면 무한급수가 반드시 수렴하는 것은 아니다.
즉, →0은 무한급수가 수렴할 수 있는 필요조건이지만 충분조건은 아니다.
<정리 3.5>의 역이 거짓임은 다음의 반례 2가지를 통해 증명된다.
2) 반례들
①반례1
②반례2
4. 다음 문제의 풀이과정과 답안을 상세하게 제시하시오. (총 8점)
1) 을 구하시오. (4점)
우변의 곱셈식에서 앞의 피승수는 약분하면 이 된다.
또한 삼각함수의 극한에서
위 곱셈식에서 승수의 분자와 분모의 x=0에서의 극한값은 각각 1이 된다.
따라서
2) 의 값을 구하기 위해 적절한 그래프의 개형을 그리고 이를 통해 답안을 유추하시오. (4점)
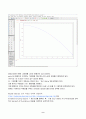
x의 값이 0.03과 1사이에서 변할 때 의 그래프를 그려보면 아래 그림과 같다.
아래 그림을 통해 알 수 있듯이 x가 0에 다가갈수록 함수값은 1에 수렴하고 있음을 알 수 있다. 실제로 wxMaxima로 x=0일 때의 극한값을 계산하면 1이 됨을 확인할 수 있다.
wxMaxima에서 평면 그래프를 그리는 명령어는 wxplot2d이다.
wxplot2d 명령어의 인자로는 그래프를 그릴 함수식과 x값의 범위를 지정해주면 된다.
여기서는 x는 0.03과 1사이의 실수 값으로 정했다.
단, 그래프를 그리기 위해서는 엔터키 대신 ‘Shift+Enter\'를 입력해야 한다.
또한 함수의 극한값은 limit 명령어를 사용한다.
이때 명령어의 인자는 함수와 극한값을 확인하고 싶은 x의 값을 위 그림처럼 입력해주면 된다.
문제는 x=0에서의 극한값을 구하는 것이므로 x값으로 0을 인자로 선택한 것이다.
참고로 wxMaxima 설치 과정을 간략히 설명한다.
https://wxmaxima-developers.github.io/wxmaxima/download.html에서
windows(including Gnuplot + Maxima)를 클릭한 후, 가장 최신 버전(5.47.0-Windows)을 선택하고 maxima-5.47.0-win64.exe 파일을 다운하여 설치하면 된다.
5. 참고문헌
장영재·이긍희·김병찬·유원석(2020) 대학수학의 이해, 방송대출판문화원
wxMaxima 사용법 동영상
https://www.youtube.com/watch?v=IctYqh6NdEc&list=PLGfO3O2Px4lFmTHUWEC2WLHEjhlA1vnbi

키워드

방송통신대대학수학의이해,   방송대대학수학의이해,   방통대대학수학의이해