Torsion 실험 레포트

소개글

Torsion 실험 레포트에 대한 보고서 자료입니다.

목차

Ⅰ. 실험 요약 5-7
1.1 실험 목적 5
1.2 이론적 배경 5-6
1.3 실험 장비 7
Ⅱ. 시험 결과 및 비교 그래프 8-13
2.1 시간-변형률 그래프 8-9
2.2 2차 그리프 구간 선정 및 최소 Creep 속도 계산 10
2.3 실험1,2에 대한 그래프 11
2.4 가공경화지수, 강도계수 계산 12
2.5 Creep의 활성화 에너지 계산 13


Ⅲ. 고찰 14

Ⅳ. 참고문헌 15

본문내용

공식
의 전단력에 의한 모멘트:
따라서
원통에서의 :
(식1)
최대 전단응력
(식2)
에서의 전단응력
(식3)
[.선형 탄성 재료로 만든 원형봉]
비틀림 각:
순수비틀림을 받는 봉의 단위 길이 당 비틀림 각
3) 시효경화 (Age Hardening)
시효경화란 금속 재료가 적정한 온도, 시간을 거치면서 인장 및 항복강도, 내마모성, 가공 용이성 향상되는 작업이다. 시효경화에는 자연시효와 인공시효가 있다.
1.3 실험 장비
1) Universal Testing Machine
[. 유니버셜 테스팅 머신]
2) 시편
TR1011(230M07) 0.15% Carbon steel
(Shear Modulus): 79 GPa
[. 시편]
2. 실험 결과 및 비교 그래프
2.1 실험 결과 계산
1) stress, strain [2]
식1에 따라 원통의 극관성 모멘트는 다음과 같다.
각도: 2.87에서 토크: 3.72Nm이다. 따라서 식2와 식4에 의해 stress와 strain을 구하면 다음과 같다.
rad
위와 같은 방법으로 다른 각도에서 stress와 strain을 계산한다.
2) 탄성영역, 항복강도
탄성영역: 탄성영역은 그래프에서 선형적인 구간을 의미한다. 따라서 선형적인 구간 까지의 각도를 구해 그 구간을 탄성영역으로 정한다.
항복강도: 항복강도의 정확한 값을 알기 어렵다. 따라서 많이 쓰는 0.2% offset method를 이용하여 항복강도를 계산한다. offset법은 선형으로 증가하는 직선을 0.2%의 변형률만큼 오프셋 해서 만들어지는 직선과 그래프가 만나는 점을 항복응력으로 하는 방법이다. 따라서 밑의 그래프에서 항복강도를 구할 수 있다. [3]
2.2 실험 결과표
1) 결과 (1)
각도( )
토크(1차)(Nm)
stress(1차)(MPa)
strain(1차)()
2.87
3.72
275.6
1.97
3.97
5.59
414.1
2.73
5.40
8.01
593.3
3.71
6.69
10.24
758.5
4.59
8.12
12.47
923.7
5.58
.
탄성 영역
항복강도(MPa)
1차
508.069
2차
87.71
3차
182.18
.
2) 결과 (2)
탄성 영역
항복강도(MPa)
1차
469.34
2차
51.68
3차
165.41
.
2.3
1) 결과(1)
2) 결과(2)
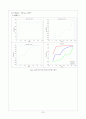
3) 결과 1과 결과 2의 종합 그래프 비교 그래프
4) 결과 (3)의 1, 2 Cycle 종합 그래프 비교 그래프
2.4 그래프의 선형성 분석
항복강도 결정을 위해 직선의 선형적인 구간을 찾아야 한다. 직선인 구간을 찾기 위해 선형성 회기 분석 방법을 사용했다. 회기분석 방법에서 직선으로 볼 수 있는 결정계수의 값은 이다. 따라서 데이터에서 결정계수가 0.98 이상인 곳의 회기분석 결과는 다음과 같다. [4]
변수
결정계수
각도()
y절편
기울기()
결과 1_1차
0.990791
15.5
-3.11331
51400.7
결과 1_2차
0.980613
64.36
-2264.89
49837.73
결과 1_3차
0.980683
11.64
-362.366
50446.78
결과 2_1차
0.982895
14.42
-36.4999
53733.94
결과 2_2차
0.980181
64.29
-2517.92
55278.59
결과 2_3차
0.986125
14.55
-516.124
56315.99
.
위의 표에서 탄성영역과 전단률을 알 수 있다.
2.5 항복강도 결정 (결과(1)과 결과(2)에서 1차, 2차, 3차)
항복강도를 결정하기 위해 offset법을 이용한다. 선형적인 구간의 기울기를 가지고 0.2%의 offset을 가지는 직선과 그래프의 교점을 메트랩을 통해 구하면 다음과 같다.
따라서 실험1의 1차에서 항복강도는 508.069MPa이다. 따라서 위의 방법으로 구해서 표로 나타내면 다음과 같다.
결과1 1차
결과1 2차
결과1 3차
결과2 1차
결과2 2차
결과2 3차
항복강도(MPa)
508.069
87.71
182.18
469.34
51.68
165.41
.
2.6 전단율 (Shear Modulus) 결정
전단률은 stress-strain 그래프에서 기울기를 의미한다.에서 선형 구간의 기울기를 구했다. 따라서 표로 정리하면 다음과 같다
1) 결과1
측정 전단율 ()
실제 전단율 ()
오차율(%)
1차
51.40
79
34.94
2차
49.84
79
36.91
3차
50.45
79
36.14
Avg
50.56
79
36.00
.
2) 결과2
측정 전단율 ()
실제 전단율 ()
오차율(%)
1차
53.73
79
31.99
2차
55.28
79
30.03
3차
56.32
79
28.71
Avg
55.11
79
30.25
.
3. 고찰
을 통해 시편에 걸리는 stress와 strain을 구하고 재료의 탄성영역과 항복강도, 전단률을 계산했다.
시편의 측정 전단률과 실제 전단률의 오차율은 결과1 36% 결과2 30.25%로 매우 큰 것을 알 수 있다. 따라서 오차의 원인을 생각하면 다음과 같다.
첫 번째 offset법의 문제이다. 전단률을 계산할 때 실제 전단률의 값을 구할 수 없다. 따라서 대체 방법인 offset법은 정확하게 전단률을 계산할 수 없어 오차가 발생한다.
두 번째 원인은 전단률 데이터의 불확실성이다. 이론상으로 stress-strain 그래프 초기에는 직선으로 나타난다. 하지만 실험 결과는 직선으로 나타나지 않고 데이터가 이산적으로 나타난다. 따라서 데이터를 직선에 근사하는 과정에서 근사방법, 오차율 설정에 따라 오차가 발생한다.
4. 참고문헌
[1]: 송동규, Torsion Test 교안
[2]:Barry J. Goodno & James M. Gere, 2020, SI재료역학, 9th editon, CENGAGE, p277~278
[3]:Barry J. Goodno & James M. Gere, 2020, SI재료역학, 9th editon, CENGAGE, p33
[4]:주희정. 2019. \"도막방수재의 장기 온도변화 및 화학침식에 의한 물성변화 연구.\" 국내박사학위논문, 동명대학교 대학원.
[Fig 1, 2, 4]: Torsion Test 교안

키워드

기계공학,   기계공학실험,   단국대학교