목차
I. 연구의 문제의식
II. 제도적 배경과 기존 문헌
1. 현행 고교 평준화 제도의 특징
2. 기존 문헌
III. 미국형 공교육 제도하의 교육균형
IV. 고교평준화 경제의 교육균형
V. 맺음말
참고문헌
II. 제도적 배경과 기존 문헌
1. 현행 고교 평준화 제도의 특징
2. 기존 문헌
III. 미국형 공교육 제도하의 교육균형
IV. 고교평준화 경제의 교육균형
V. 맺음말
참고문헌
본문내용
) - hat a )
(A3)
Z_2 ( hat a ) =F( hat a) (S_2^a (hat a ) - hat a )
(A4)
로 각각 정의하자. 이 정의를 이용할 때
Disp\' (hat a ) = f( hat a ) left { {S_1^a ( hat a ) -hat a} over {1-F( hat a )} right } + f( hat a ) left { {S_2^a ( hat a ) - hat a } over { F( hat a ) } right }
(A5)
=
f( hat a ) left { {Z_1 ( hat a ) } over {(1-F( hat a ))^2 }
+{Z_2 ( hat a ) } over {F( hat a )^2 }
right }
(A6)
=
{f( hat a ) } over {F( hat a )^2}
left { {Z_1 ( hat a ) }{ F( hat a )^2 }over {(1-F( hat a ))^2 }
+{Z_2 ( hat a ) }
right }
(A7)
으로 정리된다. 그런데
Z_1 ( hat a ) = INT _{ hat a }^{ INF } adF(a) - hat a (1-F( hat a ))
(A8)
=
left ( a F( a ) |_{ hat a }^{ INF } ~- INT _{ hat a }^{ INF } F(a)da right )- hat a (1-F( hat a ) )
(A9)
=
INT _{ hat a }^{INF } 1da - INT _{ hat a }^{INF } F(a) da = INT _{ hat a }^{ INF } (1-F(a))da
(A10)
이다. 따라서
Z_1 ( hat a )
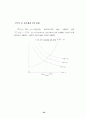
은 <그림 A3>의 빗금 친 영역,
-Z_2 ( hat a )
은 (마찬가지 과정을 거쳐) 격자무늬 영역의 크기를 각각 표시한다. 이상의 논의로부터 <그림 A4>를 얻을 수 있으며
hat a = m_a < E(a)
일 경우
Disp\'( hat a ) >0
이다. (Q.E.D)
비평준화 균형의 국지 안정성을 위한 [명제 1]의 조건 (
{hat a }^* IN N^η (m_a )
)은 일견 매우 제약적인 듯 하다. 그렇다면 이 비평준화 균형의 실현을 전제로 한 본고의 핵심 결론들은 그 타당성이 의심스러운 것은 아닐까? 이러한 의문은 추후 보다 주의 깊게 검토되어야할 주제이나 여기에서는 다음 두 가지를 지적하는 데서 논의를 마무리짓고자 한다.
첫째,
Disp\' (ρ^* ) >0
는
ρ′( {hat a}^* ) >0
보다 강한 조건이다. 즉 국지 안정성이 확보되는
{hat a}^*
의 범위는
Disp\' (ρ^* ) >0
인 영역, 즉
N^η (m_a )
보다 넓다.
둘째, 균등분포, 로그정규분포 등 상당수의 전형적 확률분포의 경우
N^η (m_a )=R_+^1
이다. 가령 <그림 A4>는 평균 1, 분산 1인 로그정규분포로부터 계산해낸 것이다. <그림 A5>와 같이 여러 가지 형태의 로그정규분포를 사용해도 점선이 굵은 실선보다 상방에 놓이는 <그림 A4>의 특징이 계속 유지됨을 확인할 수 있다.
<부록 4> 비평준화 균형의 안정성(경제적 계층이 첨가된 모형)
비평준화 균형의 국지 안정성을 충족하기 위해서는 주택 (1지역)에 대한 초과수요 함수
ED(ρ) = D(ρ) - S(ρ)
(A11)
D(ρ) = F( {{hat a}_R}^* (ρ) )+F({{hat a}_P}^* (ρ) )
(A12)
S(ρ) =[1-F( {{hat a}_R}^* (ρ) )]+[1- F({{hat a}_P}^* (ρ) )]
(A13)
와 관련하여
ED\'(ρ^* )=-2f(·)[ {{hat a}_R}^* \'(ρ^* ) + {{hat a}_P}^* \'(ρ^* )]<0
(A14)
의 부등식이 충족돼야 한다. 한편 식 (17)로부터
left ( MATRIX{ { {{hat a}_R}^* \'(ρ^* ) } # { {{hat a}_P}^* \'(ρ^* )} } right )=left [ MATRIX{ {B_RR} & {B_RP} #
# {B_PR}& {B_PP} } right ]^-1
left ( MATRIX{ {1} # #{1} } right )
, (A15)
B_cc\' = PARTIAL B_c / PARTIAL {hat a}_c\' , ~FORALL c, c\' IN C
을 도출할 수 있다. 따라서 안정성 조건, 즉 (A14)의 충족을 위해서는
{B_RR + B_PP - (B_PR + B_RP )} over Det >0, ~~Det = B_RR B_PP - B_PR B_RP
(A16)
이 필요하다. 충분조건 (A16)이 과연 얼마나 제약적인 것인지, 또 (A16)을 충족하는 것이 과연 가능한지를 엄밀히 검토하는 것은 결코 쉽지 않은 과제이다. 여기에서는 (A16)를 충족하는 구체적인 예가 존재한다는 것을 제시하는 선에서 논의를 일단 마감하고자 한다.
[例1]
a∼uniform[0,~1]
,
{tilde q}_R (x) = q_R ·x
,
{tilde q}_P (x) = q_P ·x
,
q_R > q_P
인 경우
{{hat a}_R} ^* = q_R over { q_R + q_P }
,
{{hat a}_P} ^* = q_P over { q_R + q_P }
이며
Det = Disp·(q_R +q_P )>0
,
B_RR + B_PP
-
(B_PR+ B_RP )
=
q_R q_P Disp ·[1-4 {{hat a}_R}^* ·{{hat a}_P}^* ]>0
(
{{hat a}_R}^* =1- {{hat a}_P}^* , {{hat a}_R}^* != {{hat a}_P}^*
이므로)이다. 따라서 이 [예1]은 국지 안정성의 조건 (A16)을 충족한다.
<그림 1>
재정패키지에 대한 소비자 선호의 함수 행태
<그림 2> 지역분권형 공교육제도 하에서 지역사회의 계층화
*
M_12 +M_13 = M_21 + M_31 =2/9
M_21 +M_23 = M_32 + M_12 =2/9
<그림 3> 평준화 제도 하에서 교육균형의 고정점적 특성
(P,~ S)
(H_1 , ~H_2 ,~ M_12 , ~ M_21 )
<그림 4>
(A3)
Z_2 ( hat a ) =F( hat a) (S_2^a (hat a ) - hat a )
(A4)
로 각각 정의하자. 이 정의를 이용할 때
Disp\' (hat a ) = f( hat a ) left { {S_1^a ( hat a ) -hat a} over {1-F( hat a )} right } + f( hat a ) left { {S_2^a ( hat a ) - hat a } over { F( hat a ) } right }
(A5)
=
f( hat a ) left { {Z_1 ( hat a ) } over {(1-F( hat a ))^2 }
+{Z_2 ( hat a ) } over {F( hat a )^2 }
right }
(A6)
=
{f( hat a ) } over {F( hat a )^2}
left { {Z_1 ( hat a ) }{ F( hat a )^2 }over {(1-F( hat a ))^2 }
+{Z_2 ( hat a ) }
right }
(A7)
으로 정리된다. 그런데
Z_1 ( hat a ) = INT _{ hat a }^{ INF } adF(a) - hat a (1-F( hat a ))
(A8)
=
left ( a F( a ) |_{ hat a }^{ INF } ~- INT _{ hat a }^{ INF } F(a)da right )- hat a (1-F( hat a ) )
(A9)
=
INT _{ hat a }^{INF } 1da - INT _{ hat a }^{INF } F(a) da = INT _{ hat a }^{ INF } (1-F(a))da
(A10)
이다. 따라서
Z_1 ( hat a )
은 <그림 A3>의 빗금 친 영역,
-Z_2 ( hat a )
은 (마찬가지 과정을 거쳐) 격자무늬 영역의 크기를 각각 표시한다. 이상의 논의로부터 <그림 A4>를 얻을 수 있으며
hat a = m_a < E(a)
일 경우
Disp\'( hat a ) >0
이다. (Q.E.D)
비평준화 균형의 국지 안정성을 위한 [명제 1]의 조건 (
{hat a }^* IN N^η (m_a )
)은 일견 매우 제약적인 듯 하다. 그렇다면 이 비평준화 균형의 실현을 전제로 한 본고의 핵심 결론들은 그 타당성이 의심스러운 것은 아닐까? 이러한 의문은 추후 보다 주의 깊게 검토되어야할 주제이나 여기에서는 다음 두 가지를 지적하는 데서 논의를 마무리짓고자 한다.
첫째,
Disp\' (ρ^* ) >0
는
ρ′( {hat a}^* ) >0
보다 강한 조건이다. 즉 국지 안정성이 확보되는
{hat a}^*
의 범위는
Disp\' (ρ^* ) >0
인 영역, 즉
N^η (m_a )
보다 넓다.
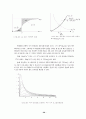
둘째, 균등분포, 로그정규분포 등 상당수의 전형적 확률분포의 경우
N^η (m_a )=R_+^1
이다. 가령 <그림 A4>는 평균 1, 분산 1인 로그정규분포로부터 계산해낸 것이다. <그림 A5>와 같이 여러 가지 형태의 로그정규분포를 사용해도 점선이 굵은 실선보다 상방에 놓이는 <그림 A4>의 특징이 계속 유지됨을 확인할 수 있다.
<부록 4> 비평준화 균형의 안정성(경제적 계층이 첨가된 모형)
비평준화 균형의 국지 안정성을 충족하기 위해서는 주택 (1지역)에 대한 초과수요 함수
ED(ρ) = D(ρ) - S(ρ)
(A11)
D(ρ) = F( {{hat a}_R}^* (ρ) )+F({{hat a}_P}^* (ρ) )
(A12)
S(ρ) =[1-F( {{hat a}_R}^* (ρ) )]+[1- F({{hat a}_P}^* (ρ) )]
(A13)
와 관련하여
ED\'(ρ^* )=-2f(·)[ {{hat a}_R}^* \'(ρ^* ) + {{hat a}_P}^* \'(ρ^* )]<0
(A14)
의 부등식이 충족돼야 한다. 한편 식 (17)로부터
left ( MATRIX{ { {{hat a}_R}^* \'(ρ^* ) } # { {{hat a}_P}^* \'(ρ^* )} } right )=left [ MATRIX{ {B_RR} & {B_RP} #
# {B_PR}& {B_PP} } right ]^-1
left ( MATRIX{ {1} # #{1} } right )
, (A15)
B_cc\' = PARTIAL B_c / PARTIAL {hat a}_c\' , ~FORALL c, c\' IN C
을 도출할 수 있다. 따라서 안정성 조건, 즉 (A14)의 충족을 위해서는
{B_RR + B_PP - (B_PR + B_RP )} over Det >0, ~~Det = B_RR B_PP - B_PR B_RP
(A16)
이 필요하다. 충분조건 (A16)이 과연 얼마나 제약적인 것인지, 또 (A16)을 충족하는 것이 과연 가능한지를 엄밀히 검토하는 것은 결코 쉽지 않은 과제이다. 여기에서는 (A16)를 충족하는 구체적인 예가 존재한다는 것을 제시하는 선에서 논의를 일단 마감하고자 한다.
[例1]
a∼uniform[0,~1]
,
{tilde q}_R (x) = q_R ·x
,
{tilde q}_P (x) = q_P ·x
,
q_R > q_P
인 경우
{{hat a}_R} ^* = q_R over { q_R + q_P }
,
{{hat a}_P} ^* = q_P over { q_R + q_P }
이며
Det = Disp·(q_R +q_P )>0
,
B_RR + B_PP
-
(B_PR+ B_RP )
=
q_R q_P Disp ·[1-4 {{hat a}_R}^* ·{{hat a}_P}^* ]>0
(
{{hat a}_R}^* =1- {{hat a}_P}^* , {{hat a}_R}^* != {{hat a}_P}^*
이므로)이다. 따라서 이 [예1]은 국지 안정성의 조건 (A16)을 충족한다.
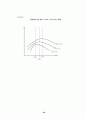
<그림 1>
재정패키지에 대한 소비자 선호의 함수 행태
<그림 2> 지역분권형 공교육제도 하에서 지역사회의 계층화
*
M_12 +M_13 = M_21 + M_31 =2/9
M_21 +M_23 = M_32 + M_12 =2/9
<그림 3> 평준화 제도 하에서 교육균형의 고정점적 특성
(P,~ S)
(H_1 , ~H_2 ,~ M_12 , ~ M_21 )
<그림 4>

















































소개글