동적기하 소프트웨어를 사용한 problem solving

목차

1. 서 론
1.1 나에게 끼친 영향
1.2 DGS는 많은 실험과 관찰을 가능하게 한다.
1.3 새로운 사고방식을 도입하게 한다. (움직이는 점)
1.4. 수학에 과학적 사고를 도입한다.

2. 문제풀이에의 적용

3. 결 론

본문내용

e A
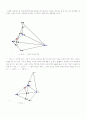
가 둔각인 경우와 마찬가지임도 확인할 수가 있다. ( < 그림 5 > , < 그림 6 > )
< 그림 4 >
< 그림 5 > < 그림 6 >
그러나,
angle C
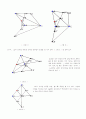
가 둔각일 경우엔 심각한 문제점이 있음을 알 수가 있다. < 그림 7 > 을 살펴 보자.
Q, R은 모두 연장선 위에 잡힐 뿐더러, P에서 Q로 쏜 빛은 반사하는 것이 아니고, 접혀서(마땅한 표현이 없네요. -_-;) R로 가는 모습을 볼 수가 있다. Q, R은 존재하지 않는 것이다. (
angle A ~또는~ angle B
가 둔각이었을 경우엔 연장선에 존재하긴 한다. )
< 그림 7 >
angle C
가 직각일 경우를 보면,
Q=R=C
임을 볼 수가 있다. 그런데, 이때를 기점으로 해서
Q, R
의 위치관계가 역전되면서 마치 허근을 보는 듯한 위치로 찍히게 되었다.
< 그림 8 >
자, 그럼 이제 본 문제에서 예각삼각형이란 조건이 왜 있어야 하는 지에 대하여 막연히 탐구를 해 본 결과가 어느 정도 정리된 듯하다. 아직은 경험적인 정당화이고 어떤 논리적인 근거는 없다. 미완성된 아까의 풀이를 완결시켜 보도록 하자.
ANGLE A , ANGLE B
가 예각이라는 조건으로부터, 선분
P' P''
은 직선
AB
와 만나지 않는다. 이로부터
P' P''
과
AC
의 교점은
A
의 오른쪽에 있을 수밖에 없게 된다. 마찬가지로
BC
와의 교점도
B
의 오른쪽에 있을 수 밖에 없다.
또한,
ANGLE P'' C P' = 2 ANGLE BCA
임을 쉽게 확인할 수가 있는데
ANGLE C
가 예각이므로
ANGLE P'' C P < 180 DEG
가 되어서
P'' P
와
AC, BC
의 교점은
C
의 왼쪽에 있어야 한다. 따라서,
Q,R
은 각각 선분
BC, CA
위에 있게 될 수 밖에 없다.
3. 결 론
본론부에서 우리는 지필환경에서 풀기 위해서는 수없이 많은 그림을 그려보고 지워보고 해야 할 것을 몇번의 마우스 드래깅만으로 해결할 수 있는 장점을 살펴 보았으며, 문제의 본질을 알기 위한 탐구를 쉽게 할 수 있는 장점도 살펴 보았다.
보다 많은 활동들을 통해서 여러가지 상황에 대한 '경험'을 하게 할 수 있으며, 그로 인해 막연한 생각들이 척척 들어맞게 되는 그런 느낌들을 갖게 해 주려면 어떻게 해야 할까는 앞으로 더 연구해 보아야 할 것이다. 그림에서 점의 위치관계가 뒤집혀도 변하지 않는 어떤 공통적인 성질(구점원에서 삼각형이 둔각삼각형이 되더라도 그 기본적인 그림은 예각삼각형일 때와 변하지 않는다던가, 어떤 두 각은 같은 크기가 되는데, 그것이 위치관계가 바뀌더라도 원주각으로 같던 것이 내대각으로 같은 것으로 바뀐다든가)에 대한 경험을 해봄으로써 수학적 개념이 확고히 되길 바란다.
또한 점들이 움직임에 따라서 움직이는 다른 점들에 대한 물리적인 사고라든가, 그림이 바뀌더라도 변하지 않는 법칙과 질서를 찾아내고, 그것을 수학적으로 증명하는 가설 및 검증이라는 과학적인 사고방식으로 수학을 재조명하게 되길 바란다.

키워드

동적기하 소프트웨어를 사용한 problem solving,   problem solving,   동적기하 소프트웨어를 사용,   컴퓨터를이용한 수학풀기,   dgs