목차
[1]
실 험 목 적
[2]
실 험 기 구
[3]
실 험 방 법
[4]
실 험 결 과
[5]
고 찰
[6]
참 고 문 헌
실 험 목 적
[2]
실 험 기 구
[3]
실 험 방 법
[4]
실 험 결 과
[5]
고 찰
[6]
참 고 문 헌
본문내용
이다.
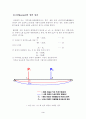
이것을 단순보에 적용시키면 다음의 그림처럼 표현되어진다.
< 그림 1.2.1 > Pi 에 먼저 하중이 가해진 경우
< 그림 1.2.2 > Pk 에 먼저 하중이 가해진 경우
위의 그림에서 나온 것을 이론에 연결시키면 외력(外力) Pi가 먼저 하중이 가해진 경우<그림 1.2.1> Pk를 추가로 가해서 δii를 δik만큼 변화시켰다고 하면, 때 변위 δik와 힘의 증가량 Pk와의 관계가 1차식을
Pk = Akiδik …… ①
로 나타낼 수 있고, i,k를 바꾼 식
Pi = Aikδki …… ②
와의 사이에
Aki = Aik …… ③
인 관계가 성립된다.
③을 다시 표현하면
라는 관계식이 성립한다.(첨자 i, k를 바꾸어도 이 식은 성립한다.)
이것이 Maxwell의 상반 정리이다.
만약 하중 Pk와 Pi가 같다면 그 변위량 δik과δki사이에는 다음과 같은 식이 성립한다.
이번 실험의 목적은 베티의 법칙 및 Maxwell의 상반 정리에 대한 이론을 이해하고 실제 실험을 통하여 이를 확인하는 것이다. 위의 두 이론은 보에서의 처짐에 관한 이론 중, 한 부분인 Maxwell의 법칙을 응용하여 실험을 진행한다.
이번 실험의 통해 이론의 개념을 정확하게 이해하고 이것이 얼마나 합리적인 원리인지 고찰해본다.
[2] 실 험 기 구
(1) 강제 빔 : 단면과 탄성계수가 일정한 강제 빔
(2) 하중 재하용 추 : 5kg짜리 1EA, 10kg짜리 1EA
(3) 다이알 게이지 : 눈금 하나당 0.01mm 용
(4) 보의 거치대 : 롤러와 힌지의 역할을 할 수 있는 것
[3] 실 험 방 법
[3.1] Betti의 법칙(<그림 3.1.1> 및 <그림 3.1.2> 참고)
(1) <그림 3.1.1>과 같이 강제빔을 양쪽 받침부 위에 올려 놓는다.
(2) 다이알 게이지를 처짐을 측정할 부분에 설치한다.
(3) 5kg의 하중을 그림과 같은 위치에 재하시킨다.
(4) 하중 재하시의 다이알 게이지의 값을 읽어 처짐량을 측정한다.
(5) 다이알 게이지를 <그림 3.1.2>과 같이 처짐을 측정할 부분에 설치한다.
(6) 10 kg의 하중을 재하시킨다.
(7) 하중 재하시의 다이알 게이지의 값을 읽어 처짐량을 측정한다.
5㎏
20㎝
다이얼
게이지 15㎝
<그림 3.1.1>
10㎏
15㎝
20 ㎝ 다이얼게이지
<그림 3.1.2>
[3.2] Maxwell의 상반정리(<그림 3.2.1> 및 <그림 3.2.2> 참고)
(1) <그림 3.2.1>과 같이 강제빔을 양쪽 받침부 위에 올려 놓는다.
(2) 다이알 게이지를 처짐을 측정할 부분에 설치한다.
(3) 5 kg의 하중을 재하시킨다.
(4) 하중 재하시의 다이알 게이지의 값을 읽어 처짐량을 측정한다.
(5) 다이알 게이지를 <그림 3.2.2>과 같이 처짐을 측정할 부분에 설치한다.
(6) 5 kg의 하중을 재하시킨다.
(7) 하중 재하시의 다이알 게이지의 값을 읽어 처짐량을 측정한다.
5㎏
20㎝
다이얼게이지
15㎝
<그림 3.2.1>
5㎏
15㎝
20㎝ 다이얼게이지
<그림 3.2.2>
[4] 실 험 결 과
[4.1] 데이터 시트(data sheet)
b-1.17㎝(왼쪽), 1.17㎝(오른쪽), 1.15(중앙)
h-2.51㎝(왼쪽), 2.48㎝(오른쪽), 2.425㎝(중앙)
I-1.366(중앙), E-2.1×㎏/㎠
실험값 [㎜]
이론값 [㎜]
Pi 일 때 δji
Pj 일 때 δij
Pi 일 때 δji
Pj 일 때 δij
Pi < Pj
0.068
0.125
0.1
0.2
비고
좌 20㎝ 우 15㎝
조건
재하하중 Pi = 5kg Pj = 10kg
강재의 탄성계수 E = 2.1 × kg/cm2
단면이차모멘트 I = 1.366cm4
- Betti의 법칙 결과
실험치 10 × 0.068 = 0.68
5 × 0.125 = 0.625
실험값 [㎜]
이론값 [㎜]
Pi 일 때 δji
Pj 일 때 δij
Pi 일 때 δji
Pj 일 때 δij
Pi = Pj
0.068
0.068
0.1
0.1
비고
좌 20㎝ 우 15㎝
조건
재하하중 Pi = 5kg Pj = 5kg
강재의 탄성계수 E = 2.1 × 10^6kg/cm2
단면이차모멘트 I = 1.366cm4
- Maxwell의 상반정리 결과
실험치 5 × 0.068= 0.34
5 × 0.068= 0.34
[4.2] 이론적 결과치
a. betti의 법칙
△(처짐량) =
△(처짐량) =
이론치 10×0.1= 1
5 × 0.2= 1
b. maxwell의 법칙
△(처짐량) =
△(처짐량) =
이론치 5 × 0.0998 = 0.5
5 × 0.10 = 0.5
[5] 고찰
실험방법은 매우 간단한 실험이어서 크게 어려움은 없었다. 하지만 Betti의 법칙과 Maxwell의 상반 정리에 대하여 이론적 지식이 많이 부족했기 때문에 처짐에 관련되 위의 법칙과 원리를 이해하는데 쉽지 않았다. 하지만 실험을 통한 결과를 비교함으로써 이론값과의 차이를 보며 막연하게 읽고 이해하는 것보다는 훨씬 나았다. 역시나 실험하는 팀을 2개로 나누어 실행했다. 이론계산을 하는 팀과 실험을 하는 팀으로 말이다. 실험방법은 이전에 시행했던 실험방법과 별 차이가 없었기 때문에 어려움은 없었다. 처짐량을 Betti의 법칙과 Maxwell의 상반 정리을 이용하여 구하는 것이므로 원하고자 하는 데이터를 측정하여 이론값과 비교하면 되는 것이었다. 공식은 어렵지 않았는데 이론적 배경이 한번에 이해가 안될만큼 난해했다. 아무튼 실험을 빨리하고 이론값과의 비교를 위해 서둘러 실험을 했다. 재하시키는 하중을 위치에 따라 놓으면서 다이얼게이지의 값을 측정하여 기록했다. 그리고 단면 2차 모멘트를 보의 높이, 폭을 통해 구하고 강재의 탄
성계수는 알고 있으므로 남은 것은 모멘트를 통한 처짐량 계산이었다. 강재에 하중을 올려 그 변위량을 비교해보면 이론값에 비해 실험값이 작게 나왔음을 알 수 있었다. 그래서 그 이유를 생각해보지 않을 수 없었다.
[6] 참 고 문 헌
김성도, 정진환, 구조공학실험, 1999, 새길
이것을 단순보에 적용시키면 다음의 그림처럼 표현되어진다.
< 그림 1.2.1 > Pi 에 먼저 하중이 가해진 경우
< 그림 1.2.2 > Pk 에 먼저 하중이 가해진 경우
위의 그림에서 나온 것을 이론에 연결시키면 외력(外力) Pi가 먼저 하중이 가해진 경우<그림 1.2.1> Pk를 추가로 가해서 δii를 δik만큼 변화시켰다고 하면, 때 변위 δik와 힘의 증가량 Pk와의 관계가 1차식을
Pk = Akiδik …… ①
로 나타낼 수 있고, i,k를 바꾼 식
Pi = Aikδki …… ②
와의 사이에
Aki = Aik …… ③
인 관계가 성립된다.
③을 다시 표현하면
라는 관계식이 성립한다.(첨자 i, k를 바꾸어도 이 식은 성립한다.)
이것이 Maxwell의 상반 정리이다.
만약 하중 Pk와 Pi가 같다면 그 변위량 δik과δki사이에는 다음과 같은 식이 성립한다.
이번 실험의 목적은 베티의 법칙 및 Maxwell의 상반 정리에 대한 이론을 이해하고 실제 실험을 통하여 이를 확인하는 것이다. 위의 두 이론은 보에서의 처짐에 관한 이론 중, 한 부분인 Maxwell의 법칙을 응용하여 실험을 진행한다.
이번 실험의 통해 이론의 개념을 정확하게 이해하고 이것이 얼마나 합리적인 원리인지 고찰해본다.
[2] 실 험 기 구
(1) 강제 빔 : 단면과 탄성계수가 일정한 강제 빔
(2) 하중 재하용 추 : 5kg짜리 1EA, 10kg짜리 1EA
(3) 다이알 게이지 : 눈금 하나당 0.01mm 용
(4) 보의 거치대 : 롤러와 힌지의 역할을 할 수 있는 것
[3] 실 험 방 법
[3.1] Betti의 법칙(<그림 3.1.1> 및 <그림 3.1.2> 참고)
(1) <그림 3.1.1>과 같이 강제빔을 양쪽 받침부 위에 올려 놓는다.
(2) 다이알 게이지를 처짐을 측정할 부분에 설치한다.
(3) 5kg의 하중을 그림과 같은 위치에 재하시킨다.
(4) 하중 재하시의 다이알 게이지의 값을 읽어 처짐량을 측정한다.
(5) 다이알 게이지를 <그림 3.1.2>과 같이 처짐을 측정할 부분에 설치한다.
(6) 10 kg의 하중을 재하시킨다.
(7) 하중 재하시의 다이알 게이지의 값을 읽어 처짐량을 측정한다.
5㎏
20㎝
다이얼
게이지 15㎝
<그림 3.1.1>
10㎏
15㎝
20 ㎝ 다이얼게이지
<그림 3.1.2>
[3.2] Maxwell의 상반정리(<그림 3.2.1> 및 <그림 3.2.2> 참고)
(1) <그림 3.2.1>과 같이 강제빔을 양쪽 받침부 위에 올려 놓는다.
(2) 다이알 게이지를 처짐을 측정할 부분에 설치한다.
(3) 5 kg의 하중을 재하시킨다.
(4) 하중 재하시의 다이알 게이지의 값을 읽어 처짐량을 측정한다.
(5) 다이알 게이지를 <그림 3.2.2>과 같이 처짐을 측정할 부분에 설치한다.
(6) 5 kg의 하중을 재하시킨다.
(7) 하중 재하시의 다이알 게이지의 값을 읽어 처짐량을 측정한다.
5㎏
20㎝
다이얼게이지
15㎝
<그림 3.2.1>
5㎏
15㎝
20㎝ 다이얼게이지
<그림 3.2.2>
[4] 실 험 결 과
[4.1] 데이터 시트(data sheet)
b-1.17㎝(왼쪽), 1.17㎝(오른쪽), 1.15(중앙)
h-2.51㎝(왼쪽), 2.48㎝(오른쪽), 2.425㎝(중앙)
I-1.366(중앙), E-2.1×㎏/㎠
실험값 [㎜]
이론값 [㎜]
Pi 일 때 δji
Pj 일 때 δij
Pi 일 때 δji
Pj 일 때 δij
Pi < Pj
0.068
0.125
0.1
0.2
비고
좌 20㎝ 우 15㎝
조건
재하하중 Pi = 5kg Pj = 10kg
강재의 탄성계수 E = 2.1 × kg/cm2
단면이차모멘트 I = 1.366cm4
- Betti의 법칙 결과
실험치 10 × 0.068 = 0.68
5 × 0.125 = 0.625
실험값 [㎜]
이론값 [㎜]
Pi 일 때 δji
Pj 일 때 δij
Pi 일 때 δji
Pj 일 때 δij
Pi = Pj
0.068
0.068
0.1
0.1
비고
좌 20㎝ 우 15㎝
조건
재하하중 Pi = 5kg Pj = 5kg
강재의 탄성계수 E = 2.1 × 10^6kg/cm2
단면이차모멘트 I = 1.366cm4
- Maxwell의 상반정리 결과
실험치 5 × 0.068= 0.34
5 × 0.068= 0.34
[4.2] 이론적 결과치
a. betti의 법칙
△(처짐량) =
△(처짐량) =
이론치 10×0.1= 1
5 × 0.2= 1
b. maxwell의 법칙
△(처짐량) =
△(처짐량) =
이론치 5 × 0.0998 = 0.5
5 × 0.10 = 0.5
[5] 고찰
실험방법은 매우 간단한 실험이어서 크게 어려움은 없었다. 하지만 Betti의 법칙과 Maxwell의 상반 정리에 대하여 이론적 지식이 많이 부족했기 때문에 처짐에 관련되 위의 법칙과 원리를 이해하는데 쉽지 않았다. 하지만 실험을 통한 결과를 비교함으로써 이론값과의 차이를 보며 막연하게 읽고 이해하는 것보다는 훨씬 나았다. 역시나 실험하는 팀을 2개로 나누어 실행했다. 이론계산을 하는 팀과 실험을 하는 팀으로 말이다. 실험방법은 이전에 시행했던 실험방법과 별 차이가 없었기 때문에 어려움은 없었다. 처짐량을 Betti의 법칙과 Maxwell의 상반 정리을 이용하여 구하는 것이므로 원하고자 하는 데이터를 측정하여 이론값과 비교하면 되는 것이었다. 공식은 어렵지 않았는데 이론적 배경이 한번에 이해가 안될만큼 난해했다. 아무튼 실험을 빨리하고 이론값과의 비교를 위해 서둘러 실험을 했다. 재하시키는 하중을 위치에 따라 놓으면서 다이얼게이지의 값을 측정하여 기록했다. 그리고 단면 2차 모멘트를 보의 높이, 폭을 통해 구하고 강재의 탄
성계수는 알고 있으므로 남은 것은 모멘트를 통한 처짐량 계산이었다. 강재에 하중을 올려 그 변위량을 비교해보면 이론값에 비해 실험값이 작게 나왔음을 알 수 있었다. 그래서 그 이유를 생각해보지 않을 수 없었다.
[6] 참 고 문 헌
김성도, 정진환, 구조공학실험, 1999, 새길






























소개글