본문내용
(s)##
THEREFORE H(s) = {A(s)B(s)D(s)} over { 1 +A(s)B(s)C(s)}
7-12.
(a) 전체 시스템의 전달 함수는
H_s (s) + H_2 (s)
이고 임펄스 신호에 대한 출력 신호가 임펄스 응답이므로
H_s (s) + H_2 (s)
에 대한 라플라스 역변환을 구하면 된다. 단, 각 임펄스 응답이 Right-Sided 신호이므로 ROC는 반드시 s-영역의 오른쪽 부분이 된다. 표 7.2에 의하여
h_1 (t) = te^-2t u(t), ~h_2 (t) = 2 e^-2t u(t)
이므로 출력 신호는
y (t) = te^-2t u(t) + 2 e^-2t u(t)
이다.
(b)
Y(s) = 5 over 4 1 over s - 5 over 4 1 over s+2 - 1 over 2 1 over {(s+2)^2} = {2s + 5} over {s(s+2)^2}, Re LEFT{ s RIGHT} > 0##
H(s) = 1 over {(s+2)^2} + 2 over s+2 = {2s + 5} over {(s+2)^2}, Re LEFT{ s RIGHT} > -2##
X(s) = Y(s) over H(s) = 1 over s , Re LEFT{ s RIGHT} > 0##
THEREFORE x(t) = u(t)
7-13.
(a) 극점이
s = -0.5 +- j
이므로
H(s) = G over {(s+0.5+j)(s+0.5-j)} = G over {(s+0.5)^2 + 1}
이다.
H(0) = 1
조건을 만족하도록 이득
G
값을 구하면
H(0) = G over {0.5^2 + 1} = G over 1.25 = 1
,
G = 1.25
이고, 최종
H(s) = 1.25 over {(s+0.5)^2 + 1}
이다.
(b) 극점이
s = -0.5 +- j
, 영점
s = +- j 0.5
이므로
H(s) = G {(s-j 0.5)(s+j 0.5)}over {(s+0.5+j)(s+0.5-j)} = G {s^2 + 0.25} over {(s+0.5)^2 + 1}
이다.
H(0) = 1
조건을 만족하도록 이득
G
값을 구하면
H(0) = G 0.25 over {0.25 + 1} = G 0.25 over 1.25 = 1
,
G = 5
이고, 최종
H(s) = 5 {s^2 + 0.25} over {(s+0.5)^2 + 1}
이다.
(c) 극점이
s = -0.1 +- j0.5
, 영점
s = +- j
이므로
H(s) = G {(s-j)(s+j)}over {(s+0.1+j0.5)(s+0.1-j0.5)} = G {s^2 + 1} over {(s+0.1)^2 + 0.25}
이다.
H(0) = 1
조건을 만족하도록 이득
G
값을 구하면
H(s) = G {1} over {0.1^2 + 0.25} = G over 0.26 = 1
,
G = 0.26
이고, 최종
H(s) = 0.26 {s^2 + 1} over {(s+0.1)^2 + 0.25}
이다.
7-14.
(a)
s = j OMEGA
에 따라 움직이면서
|H( OMEGA) | = |G| { PROD from i=1 to R ( j OMEGA 와~ 영점까지의~ 거리 )} over
{ PROD from k=1 to P ( j OMEGA 와~ 극점까지의~ 거리 ) }
를 계산하면 극점 근처에서 최대값을 가지며 다음과 같은 모양을 가진다.
(b)
s = +- j 0.5
에서
| H(OMEGA) | = 0
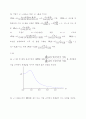
이 되고, 극점 근처에서 최대값이 되는 모양을 가진다.
(c)
s = +- j
에서
| H(OMEGA) | = 0
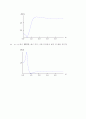
이 되고, 극점 근처에서 매우 큰 값을 가진다.
THEREFORE H(s) = {A(s)B(s)D(s)} over { 1 +A(s)B(s)C(s)}
7-12.
(a) 전체 시스템의 전달 함수는
H_s (s) + H_2 (s)
이고 임펄스 신호에 대한 출력 신호가 임펄스 응답이므로
H_s (s) + H_2 (s)
에 대한 라플라스 역변환을 구하면 된다. 단, 각 임펄스 응답이 Right-Sided 신호이므로 ROC는 반드시 s-영역의 오른쪽 부분이 된다. 표 7.2에 의하여
h_1 (t) = te^-2t u(t), ~h_2 (t) = 2 e^-2t u(t)
이므로 출력 신호는
y (t) = te^-2t u(t) + 2 e^-2t u(t)
이다.
(b)
Y(s) = 5 over 4 1 over s - 5 over 4 1 over s+2 - 1 over 2 1 over {(s+2)^2} = {2s + 5} over {s(s+2)^2}, Re LEFT{ s RIGHT} > 0##
H(s) = 1 over {(s+2)^2} + 2 over s+2 = {2s + 5} over {(s+2)^2}, Re LEFT{ s RIGHT} > -2##
X(s) = Y(s) over H(s) = 1 over s , Re LEFT{ s RIGHT} > 0##
THEREFORE x(t) = u(t)
7-13.
(a) 극점이
s = -0.5 +- j
이므로
H(s) = G over {(s+0.5+j)(s+0.5-j)} = G over {(s+0.5)^2 + 1}
이다.
H(0) = 1
조건을 만족하도록 이득
G
값을 구하면
H(0) = G over {0.5^2 + 1} = G over 1.25 = 1
,
G = 1.25
이고, 최종
H(s) = 1.25 over {(s+0.5)^2 + 1}
이다.
(b) 극점이
s = -0.5 +- j
, 영점
s = +- j 0.5
이므로
H(s) = G {(s-j 0.5)(s+j 0.5)}over {(s+0.5+j)(s+0.5-j)} = G {s^2 + 0.25} over {(s+0.5)^2 + 1}
이다.
H(0) = 1
조건을 만족하도록 이득
G
값을 구하면
H(0) = G 0.25 over {0.25 + 1} = G 0.25 over 1.25 = 1
,
G = 5
이고, 최종
H(s) = 5 {s^2 + 0.25} over {(s+0.5)^2 + 1}
이다.
(c) 극점이
s = -0.1 +- j0.5
, 영점
s = +- j
이므로
H(s) = G {(s-j)(s+j)}over {(s+0.1+j0.5)(s+0.1-j0.5)} = G {s^2 + 1} over {(s+0.1)^2 + 0.25}
이다.
H(0) = 1
조건을 만족하도록 이득
G
값을 구하면
H(s) = G {1} over {0.1^2 + 0.25} = G over 0.26 = 1
,
G = 0.26
이고, 최종
H(s) = 0.26 {s^2 + 1} over {(s+0.1)^2 + 0.25}
이다.
7-14.
(a)
s = j OMEGA
에 따라 움직이면서
|H( OMEGA) | = |G| { PROD from i=1 to R ( j OMEGA 와~ 영점까지의~ 거리 )} over
{ PROD from k=1 to P ( j OMEGA 와~ 극점까지의~ 거리 ) }
를 계산하면 극점 근처에서 최대값을 가지며 다음과 같은 모양을 가진다.
(b)
s = +- j 0.5
에서
| H(OMEGA) | = 0
이 되고, 극점 근처에서 최대값이 되는 모양을 가진다.
(c)
s = +- j
에서
| H(OMEGA) | = 0
이 되고, 극점 근처에서 매우 큰 값을 가진다.
추천자료
 멀티미디어 데이터의 처리 - 7장 연습문제 풀이 -
멀티미디어 데이터의 처리 - 7장 연습문제 풀이 - a book on c 2장 연습문제 풀이
a book on c 2장 연습문제 풀이 운영체제(공룡책) 연습문제 1장 답
운영체제(공룡책) 연습문제 1장 답 운영체제(공룡책) 연습문제 2장 System Structures 답
운영체제(공룡책) 연습문제 2장 System Structures 답 [ARENA,시뮬레이션,연습문제,솔류션,simulation] ARENA를 이용한 시뮬레이션 3장 11,12번 솔루션
[ARENA,시뮬레이션,연습문제,솔류션,simulation] ARENA를 이용한 시뮬레이션 3장 11,12번 솔루션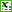 기초수문학 (용문각) 6장 연습문제
기초수문학 (용문각) 6장 연습문제  기초수문학 (용문각) 7장 연습문제
기초수문학 (용문각) 7장 연습문제  (사용자중심의) 관리회계2,3장 - 연습문제 해답
(사용자중심의) 관리회계2,3장 - 연습문제 해답 (창민사)민성기 재무관리원론 연습문제 2,3장
(창민사)민성기 재무관리원론 연습문제 2,3장  인간공학 1장, 2장, 3장 연습문제 풀이
인간공학 1장, 2장, 3장 연습문제 풀이 공학경제(교우사) 2~5장 연습문제 풀이(솔루션)
공학경제(교우사) 2~5장 연습문제 풀이(솔루션)  IT융합 시대의 멀티미디어 배움터 2.0 1장.2장 연습문제
IT융합 시대의 멀티미디어 배움터 2.0 1장.2장 연습문제 1장. 리눅스의 기본 개념과 프로그램 작성 연습문제
1장. 리눅스의 기본 개념과 프로그램 작성 연습문제 [레포트] 수문학 5장 연습문제 풀이
[레포트] 수문학 5장 연습문제 풀이



























소개글