통신이론 매틀랩 프로젝트(AM변조복조)

소개글

통신이론 매틀랩 프로젝트(AM변조복조)에 대한 보고서 자료입니다.

목차

1.1.2 Plot the spectra of m(t) and u1(t)

1.1.4 Demodulate the modulated signal u1(t) and recover m(t). Plot the result in the time and frequency domains.

1.2.2 Plot the spectra of m(t) and u2(t).

1.2.4 Demodulate the modulated signal u2(t) and recover m(t). Plot the results in the time and frequency domains.

2. [SSB-AM & VSB-AM]
2.1.1 Plot the Hilbert transform of the message signal and the modulated signal u3(t). Also plot the spectrum of the modulated signal u3(t) and compare with the spectrum of the DSB-SC AM modulated signal u1(t).

2.1.3 Demodulate the modulated signal u3(t) and recover m(t). Plot the results in the time and frequency domains.

본문내용

y
a=0.85; %Modulation index
fs = 1/ts; %Sample Frequency
t=[0:ts:t0]; %Time Vector
df=0.25; %Desired Frequency
%message signal
%sample의 0부터 0.05까지 1, 0.51부터 0.10까지 -2, 그 뒤로 0값을 갖는 벡터
m=[ones(1,t0/(3*ts)+1),-2*ones(1,t0/(3*ts)), zeros(1,t0/(3*ts))];
c=cos(2*pi*fc.*t); %캐리어 시그널
m_n=m/max(abs(m)); %Normalizing
u=(1+a*m_n).*c; %modulating
y=(u.*c)*2-1; %Demodulation
[Y,y,df1]=fftseq(y,ts,df); %Fourier Transform
Y=Y/fs; %Sample 수 만큼 나눠준다
n_cut=floor(200/df1); %filter design frequency 200에서 짤라준다
f=[0:df1:df1*(length(y)-1)]-fs/2; %Frequency vector
F=zeros(size(f)); %filter vector
F(1:n_cut)=2*ones(1,n_cut);
F(length(f)-n_cut+1:length(f))=2*ones(1,n_cut);
D=F.*Y; %filter 통과
dem=real(ifft(D))*fs; %Demodulate Signal
clf
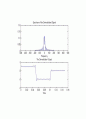
subplot(2,1,1) %주파수 축에서의 복조 시그널
plot(f,fftshift(abs(D)))
title('Spectrum of the Demodulated Signal')
xlabel('Frequency')
subplot(2,1,2) %시간 축에서의 복조 시그널
plot(t,dem(1:length(t)))
title('The Demodulator Output')
xlabel('Time')
2. [SSB-AM & VSB-AM]
2.1.1 Plot the Hilbert transform of the message signal and the modulated signal u3(t). Also plot the spectrum of the modulated signal u3(t) and compare with the spectrum of the DSB-SC AM modulated signal u1(t).
echo on
t0=0.15;
ts=0.001; %샘플 시간
fc=250; %Frequency
fs=1/ts; %Sample Frequency
df=0.25; %Desired Frequency
t=[0:ts:t0]; %time vector
%message signal
%sample의 0부터 0.05까지 1, 0.51부터 0.10까지 -2, 그 뒤로 0값을 갖는 벡터
m=[ones(1,t0/(3*ts)+1),-2*ones(1,t0/(3*ts)),zeros(1,t0/(3*ts))];
u=m.*cos(2*pi*fc.*t)+imag(hilbert(m)).*sin(2*pi*fc.*t); %LSSB SIGNAL
f=[0:df1:df1*(length(u)-1)]-fs/2; %Frequency Vector
[U,u,df1]=fftseq(u,ts,df);
U=U/fs;
f=[0:df1:df1*(length(u)-1)]-fs/2;
clf
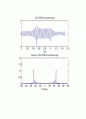
subplot(2,1,1)
plot(t,u(1:length(t)))
xlabel('Time')
title('The LSSB-AM modulated signal')
subplot(2,1,2)
plot(f,abs(fftshift(U)))
xlabel('Frequency')
title('Spectrum of the LSSB-AM modulated signal')
2.1.3 Demodulate the modulated signal u3(t) and recover m(t). Plot the results in the time and frequency domains.
echo on
t0=0.15;
ts=0.001; %샘플 시간
fc=250; %Frequency
fs=1/ts; %Sample Frequency
df=0.25; %Desired Frequency
t=[0:ts:t0]; %time vector
%message signal
%sample의 0부터 0.05까지 1, 0.51부터 0.10까지 -2, 그 뒤로 0값을 갖는 벡터
m=[ones(1,t0/(3*ts)+1),-2*ones(1,t0/(3*ts)),zeros(1,t0/(3*ts))];
u=m.*cos(2*pi*fc.*t)+imag(hilbert(m)).*sin(2*pi*fc.*t); %LSSB SIGNAL
f=[0:df1:df1*(length(u)-1)]-fs/2; %Frequency Vector
c=cos(2*pi*fc.*t) %Demodulator ocilator signal
y=(u.*c); %Demodulation
[Y,y,df1]=fftseq(y,ts,df); %Fourier Transform
Y=Y/fs; %Sample 수 만큼 나눠준다
n_cut=floor(200/df1); %filter design frequency 200에서 짤라준다
f=[0:df1:df1*(length(y)-1)]-fs/2; %Frequency vector
F=zeros(size(f)); %filter vector
F(1:n_cut)=2*ones(1,n_cut);
F(length(f)-n_cut+1:length(f))=2*ones(1,n_cut);
D=F.*Y; %filter 통과
dem=real(ifft(D))*fs; %Demodulate Signal
clf
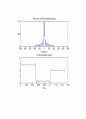
subplot(2,1,1) %주파수 축에서의 복조 시그널
plot(f,fftshift(abs(D)))
title('Spectrum of the Demodulated Signal')
xlabel('Frequency')
subplot(2,1,2) %시간 축에서의 복조 시그널
plot(t,dem(1:length(t)))
title('The Demodulator Output')
xlabel('Time')

키워드

매틀랩,   AM변조,   AM복조,   통신이론,   프로젝트,   통신 프로젝트