수치해석 - Runge-Kutta법

소개글

수치해석 - Runge-Kutta법에 대한 보고서 자료입니다.

목차

● 문 제

● 풀 이

● 고 찰

본문내용

0.02:2
z=exp(1/3*t.^3-1.2*t)
hold on
plot(t,z)
xlabel('x')
ylabel('y')
title('RK-4 & TRUE Value graph');
legend('RK-4','True',0);
Matlab Graph
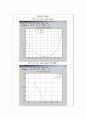
RK-4 & True value graph
RK-4 & True value graph 부분확대 1
Matlab Graph
RK-4 & True value graph 부분확대 2
● 고 찰
전산수치해석 수업의 마지막 부분이라고 할 수 있는 상미분 방정식의 Runge-Kutta법을 교수님께 배우고 연습문제 프로그램을 짜 보았다. 먼저 손으로 풀 수 있는 상미분 방정식인가 확인한다. 여기서는 손으로 직접 풀 수 있으나 RK-4를 프로그램으로 짜보는 연습이므로 손으로 풀 수 없다고 가정하고 수치해에 접근한다. 이 상미분 방정식을 손으로 풀면 이 나온다. 이 식에 x = 0부터 x = 2.0까지 0.5단위로 넣고 매틀랩으로 선-그래프를 그린 후 그 위에 RK-4로 푼 점들을 찍어 보았다. 그 결과, 결과값들을 비교하기 힘들만큼 - 그래프상 보이는 True value와 RK-4 - True value와 RK-4는 거의 같은 값을 가졌고 C language를 통한 해석에서도 True value와 RK-4 의 결과는 가장 큰가 0.5%정도로 RK-4는 정확성을 가졌다. - 보통은 0.03미만의 값을 가졌다. - 교수님께서 설명하셨듯이 RK-4는 매우 정확성을 가지는 상미분 해법 방식으로 내 눈으로 확인하고 RK-4를 프로그램으로 한번 coding해보는 의미를 가졌다.

키워드

수치해석,   Runge-Kutta법,   RK,   R-K,   Runge-Kutta