
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
-
11
-
12
-
13
-
14
-
15
-
16
-
17
-
18
-
19
-
20
-
21
-
22
-
23
-
24
-
25
-
26
-
27
-
28
-
29
-
30
-
31
-
32
-
33
-
34
-
35
-
36
-
37
-
38
-
39
-
40
-
41
-
42
-
43
-
44
-
45
-
46
-
47
-
48
-
49
-
50


본문내용
든 전자에 대해서 금속의 일함수에 해당하는 전자 결합 에너지를 구한다(binding energy)
③모든 원자의 전자를 모두 떼어가면서 측정
Bohr의 원자 모형(Planet Model)
각운동량 양자화 가설이라는 말과 전자의 궤도는 양자화 되어있다는 가정은 양자역학적이지만
양자역학적 원자 model은 아니다.
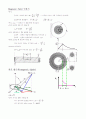
①전자들은 핵 주위를 등속원운동 한다.(구심력=핵과 전자사이의 정전기적 인력)
②전자들은 정해진 핵 전자거리를 갖는다.(orbit)
전자의 energy는 운동E(전자의 원운동에 의한 운동 에너지)와 위치E(핵과 전자 사이의 정전기적 인력에 의한 위치 에너지)로 구성된다.
①전체E=위치E+운동E
②핵과 전자 사이의 electric potential energy는 계산 가능하고 전기적 인력이 유일한 구심력이므로 운동 에너지 계산 가능
에너지 준위, 각운동량, 궤도 양자화 가설
①발머 식을 만족시키기 위하여 → 에너지 준위가 양자화 되어있어야 하고 → 각 운동량이 양자화 되어있어야 하고 → 정해진 핵 전자 거리를 가져야 한다.
②에너지 준위 양자화
는 리드베리 상수 = 수소 원자가 바닥 상태에 있을 때의 에너지
③반지름 양자화
는 보어 반지름 = 수소 원자의 바닥 상태 반지름
④고전역학적으로 보면 반지름 양자화=에너지 준위 양자화=각운동량 양자화가 동일하지만
실제로는 에너지 준위만 양자화 된다.
스펙트럼선의 설명
①발머의 해석 :
②보어의 해석 :
최소 파장 빛(최대E)이 방출 되는 경우
①시작 궤도가 같으면 작을수록 최소 파장이 방출된다.
②값이 클수록? 틀린말
③값이 클수록
→ 시험에서는 값을 모르더라도 비례 이용해서 계산이 가능하도록 낸다.
ex. 수소 원자의 바닥 상태(n=1)의 에너지를 준다던가
전자가 1개만 있는 원자에서 모두 적용된다. : H, He+, Li2+, Be3+
ex. Li2+ ion의 경우 이므로
드브로이의 물질파 이론 때문에 전자가 파동 운동을 해야하고 파동 함수에 의해서만 해석이 가능해 지면서 깨진다. → 불과 10년만에 제자들에 의해 완전히 깨지지만 Bohr 연구소에서 양자역학을 태동시키도록 유도하였다.
드브로이 물질파
1924년 프랑스의 Louis de Broglie : 운동하는 입자는 파동의 성질을 갖게 된다.
pf. 전자 빔의 회절 등
where 는 운동량
일상 수준에서는 느낄 수 없으나(too small)
원자내 전자의 경우는 문제됨()
정상파(standing wave) : 배와 마디(node)가 있고 제자리에서 진동하는 것 → 매우 안정함
cf. 진행파(travelling wave)
보어모델에서 만약 전자가 원운동을 한다면 방사선을 방출하며 E 잃어버리면서 핵에 충돌한다는 문제점(방사광 가속기에서 방출되는 x ray 처럼)이 있다. → 그러므로 원운동 하지 않는다.
①전자의 물질파
②정상파 조건
→ 각운동량 양자화의 진정한 의미
③전자는 원운동하는 입자가 아니고 원궤도 상의 안정한 정상파이다.
Heisenberg의 불확정성 원리
운동하는 물체의 위치와 운동량을 정확히 정하는 것은 불가능하다.
①우리가 측정하려면 운동량이나 위치는 알아야 하나를 바탕으로 우리가 준 운동량을 더하거나 빼서 다른 것을 계산할 수 있는데 둘 다 모를 때는 동시에 결정이 불가능하다.
②우리가 잴 수 있는 도구 자체가 양자화 되어있기 때문이다.
1927년 Werner Heisenberg : 전자가 어디있고 그 궤도가 어떤지를 정확하게 규정할 수 없다. 최소 불확정성 존재 → 정상파 조건에 의한 각운동량에서 n=1 때의 절반
파동 함수
원자내 전자의 위치는 파동함수로 나타내어야
파동 함수
①공간상에 define된 확률 밀도함수로서 orbital이라 한다.
②파동함수의 위상이 그곳에 위치하고 있을 확률과 관련됨
③파동함수 수립을 위해 파동 방정식을 먼저 푼다.
④위치에 따른 존재 확률 (파동함수의 진폭)2
비례한다고만 한 이유는 공간상에서 전부 적분하면 1이 되어야 하기 때문이다.
오스트리아의 Erwin Schrdinger
①파동함수(오비탈) : 확률 밀도함수로서 제곱값이 주어진 공간에서 전자를 발견할 확률이다.
②파동 방정식 : 원자 내 전자위치에 대한 파동 함수를 세우기 위한 방정식
②해 : 에너지와 위치에 관한 경우의 수들이 나온다.
1차원 무한 포텐셜 우물에서의 파동 함수 계산
파동 함수를 로 놓자.
혹은 인 점에서 확률은 0이 되어야 하므로 이어야 한다.
파동함수의 제곱은 확률 밀도 함수이므로 을 사용하여 A를 구한다.
에너지 연산자를 적용하며 eigenvalue를 구하면 이 된다.
대응 원리
양자역학적 결과의 극한값이 고전역학적 결과와 같다.
궤도의 개수가 한정되어있다고 보지 않고 무한개가 있다고 보거나
플랑크 상수를 0으로 보내거나 하는 기법을 쓴다.
위의 무한 포텐셜 우물의 경우 대응 원리를 쓰면 , 인 곳을 제외하고 모두 동일한 확률로 전자가 발견될 것이라는 결과를 얻는다.
전자스핀과 파울리의 베타원리
선스펙트럼을 상세히 관찰 → 아주 근접한 2쌍의 스펙트럼 발견
네 번째 양자수 : 전자의 자전방향을 나타냄 ↑또는 ↓
1925년 오스트리아의 Wolfgang Pauli의 exclusion Principle
원자 안에 있는 두 개의 전자는 4개의 양자수가 모두 같을 수는 없다.
오비탈에는 전자가 2개 까지 들어갈 수 있다.
Aufban의 원리
①낮은 에너지의 orbital부터 채운다.
②Pauli : 한 orbital에는 spin이 다른 두 개의 전자만을 채울 수 있다.
③Hund의 규칙 : 만일 여러개의 orbital이 같은 에너지 준위를 가지면(축퇴, degererate) 모든 orbital들이 채워질 때 까지 한 개의 전자씩 채워들어간다. 이 때 하나씩 채워진 전자는 모두 같은 spin을 갖는다.
예외
Cr : [Ar]4s23d4(x)
[Ar]4s13d5(o)
4s에 있는 전자를 에너지 준위가 비슷한 3d로 옮기면서 완전히 채워진 부껍질을 두 개의 반만 채워진 부껍질로 교환
Cu : [Ar]4s23d9(x)
[Ar]4s13d10(o)
이와 같은 현상은 부껍질 내의 전자-전자 반발력 때문이다.(pairing energy)
③모든 원자의 전자를 모두 떼어가면서 측정
Bohr의 원자 모형(Planet Model)
각운동량 양자화 가설이라는 말과 전자의 궤도는 양자화 되어있다는 가정은 양자역학적이지만
양자역학적 원자 model은 아니다.
①전자들은 핵 주위를 등속원운동 한다.(구심력=핵과 전자사이의 정전기적 인력)
②전자들은 정해진 핵 전자거리를 갖는다.(orbit)
전자의 energy는 운동E(전자의 원운동에 의한 운동 에너지)와 위치E(핵과 전자 사이의 정전기적 인력에 의한 위치 에너지)로 구성된다.
①전체E=위치E+운동E
②핵과 전자 사이의 electric potential energy는 계산 가능하고 전기적 인력이 유일한 구심력이므로 운동 에너지 계산 가능
에너지 준위, 각운동량, 궤도 양자화 가설
①발머 식을 만족시키기 위하여 → 에너지 준위가 양자화 되어있어야 하고 → 각 운동량이 양자화 되어있어야 하고 → 정해진 핵 전자 거리를 가져야 한다.
②에너지 준위 양자화
는 리드베리 상수 = 수소 원자가 바닥 상태에 있을 때의 에너지
③반지름 양자화
는 보어 반지름 = 수소 원자의 바닥 상태 반지름
④고전역학적으로 보면 반지름 양자화=에너지 준위 양자화=각운동량 양자화가 동일하지만
실제로는 에너지 준위만 양자화 된다.
스펙트럼선의 설명
①발머의 해석 :
②보어의 해석 :
최소 파장 빛(최대E)이 방출 되는 경우
①시작 궤도가 같으면 작을수록 최소 파장이 방출된다.
②값이 클수록? 틀린말
③값이 클수록
→ 시험에서는 값을 모르더라도 비례 이용해서 계산이 가능하도록 낸다.
ex. 수소 원자의 바닥 상태(n=1)의 에너지를 준다던가
전자가 1개만 있는 원자에서 모두 적용된다. : H, He+, Li2+, Be3+
ex. Li2+ ion의 경우 이므로
드브로이의 물질파 이론 때문에 전자가 파동 운동을 해야하고 파동 함수에 의해서만 해석이 가능해 지면서 깨진다. → 불과 10년만에 제자들에 의해 완전히 깨지지만 Bohr 연구소에서 양자역학을 태동시키도록 유도하였다.
드브로이 물질파
1924년 프랑스의 Louis de Broglie : 운동하는 입자는 파동의 성질을 갖게 된다.
pf. 전자 빔의 회절 등
where 는 운동량
일상 수준에서는 느낄 수 없으나(too small)
원자내 전자의 경우는 문제됨()
정상파(standing wave) : 배와 마디(node)가 있고 제자리에서 진동하는 것 → 매우 안정함
cf. 진행파(travelling wave)
보어모델에서 만약 전자가 원운동을 한다면 방사선을 방출하며 E 잃어버리면서 핵에 충돌한다는 문제점(방사광 가속기에서 방출되는 x ray 처럼)이 있다. → 그러므로 원운동 하지 않는다.
①전자의 물질파
②정상파 조건
→ 각운동량 양자화의 진정한 의미
③전자는 원운동하는 입자가 아니고 원궤도 상의 안정한 정상파이다.
Heisenberg의 불확정성 원리
운동하는 물체의 위치와 운동량을 정확히 정하는 것은 불가능하다.
①우리가 측정하려면 운동량이나 위치는 알아야 하나를 바탕으로 우리가 준 운동량을 더하거나 빼서 다른 것을 계산할 수 있는데 둘 다 모를 때는 동시에 결정이 불가능하다.
②우리가 잴 수 있는 도구 자체가 양자화 되어있기 때문이다.
1927년 Werner Heisenberg : 전자가 어디있고 그 궤도가 어떤지를 정확하게 규정할 수 없다. 최소 불확정성 존재 → 정상파 조건에 의한 각운동량에서 n=1 때의 절반
파동 함수
원자내 전자의 위치는 파동함수로 나타내어야
파동 함수
①공간상에 define된 확률 밀도함수로서 orbital이라 한다.
②파동함수의 위상이 그곳에 위치하고 있을 확률과 관련됨
③파동함수 수립을 위해 파동 방정식을 먼저 푼다.
④위치에 따른 존재 확률 (파동함수의 진폭)2
비례한다고만 한 이유는 공간상에서 전부 적분하면 1이 되어야 하기 때문이다.
오스트리아의 Erwin Schrdinger
①파동함수(오비탈) : 확률 밀도함수로서 제곱값이 주어진 공간에서 전자를 발견할 확률이다.
②파동 방정식 : 원자 내 전자위치에 대한 파동 함수를 세우기 위한 방정식
②해 : 에너지와 위치에 관한 경우의 수들이 나온다.
1차원 무한 포텐셜 우물에서의 파동 함수 계산
파동 함수를 로 놓자.
혹은 인 점에서 확률은 0이 되어야 하므로 이어야 한다.
파동함수의 제곱은 확률 밀도 함수이므로 을 사용하여 A를 구한다.
에너지 연산자를 적용하며 eigenvalue를 구하면 이 된다.
대응 원리
양자역학적 결과의 극한값이 고전역학적 결과와 같다.
궤도의 개수가 한정되어있다고 보지 않고 무한개가 있다고 보거나
플랑크 상수를 0으로 보내거나 하는 기법을 쓴다.
위의 무한 포텐셜 우물의 경우 대응 원리를 쓰면 , 인 곳을 제외하고 모두 동일한 확률로 전자가 발견될 것이라는 결과를 얻는다.
전자스핀과 파울리의 베타원리
선스펙트럼을 상세히 관찰 → 아주 근접한 2쌍의 스펙트럼 발견
네 번째 양자수 : 전자의 자전방향을 나타냄 ↑또는 ↓
1925년 오스트리아의 Wolfgang Pauli의 exclusion Principle
원자 안에 있는 두 개의 전자는 4개의 양자수가 모두 같을 수는 없다.
오비탈에는 전자가 2개 까지 들어갈 수 있다.
Aufban의 원리
①낮은 에너지의 orbital부터 채운다.
②Pauli : 한 orbital에는 spin이 다른 두 개의 전자만을 채울 수 있다.
③Hund의 규칙 : 만일 여러개의 orbital이 같은 에너지 준위를 가지면(축퇴, degererate) 모든 orbital들이 채워질 때 까지 한 개의 전자씩 채워들어간다. 이 때 하나씩 채워진 전자는 모두 같은 spin을 갖는다.
예외
Cr : [Ar]4s23d4(x)
[Ar]4s13d5(o)
4s에 있는 전자를 에너지 준위가 비슷한 3d로 옮기면서 완전히 채워진 부껍질을 두 개의 반만 채워진 부껍질로 교환
Cu : [Ar]4s23d9(x)
[Ar]4s13d10(o)
이와 같은 현상은 부껍질 내의 전자-전자 반발력 때문이다.(pairing energy)
추천자료
 [일반물리학실험] 자유낙하와 포물선운동 실험
[일반물리학실험] 자유낙하와 포물선운동 실험 [일반물리학실험] 등속원운동과 구심력 실험 예비레포트
[일반물리학실험] 등속원운동과 구심력 실험 예비레포트 [일반물리학실험] 마찰력과 마찰계수 측정 실험 및 결과고찰
[일반물리학실험] 마찰력과 마찰계수 측정 실험 및 결과고찰 [일반물리학실험] 강체의 단진동 예비보고서
[일반물리학실험] 강체의 단진동 예비보고서 자기유도(전류천칭)<일반물리학실험//형설출판사//경희대학교>
자기유도(전류천칭)<일반물리학실험//형설출판사//경희대학교> [일반물리학실험] 전류와자기장 예비레포트
[일반물리학실험] 전류와자기장 예비레포트 일반물리학실험 - 컴퓨터 화상실험2(입자의 산란)(예비, 결과)
일반물리학실험 - 컴퓨터 화상실험2(입자의 산란)(예비, 결과) [Solution] 일반물리학8판 솔루션(Ch1 ~ 39)
[Solution] 일반물리학8판 솔루션(Ch1 ~ 39) [일반물리학] 비탈면에서의 가속도 측정 - 실험목적, 관련이론, 계획, 결과 및 고찰
[일반물리학] 비탈면에서의 가속도 측정 - 실험목적, 관련이론, 계획, 결과 및 고찰 유도기 전력(코일을 통과한 자석) 일반물리학 북스힐 2012최신개정판
유도기 전력(코일을 통과한 자석) 일반물리학 북스힐 2012최신개정판 일반물리학 - 운동량 보존 실험
일반물리학 - 운동량 보존 실험 일반물리학 실험 - 전류천칭
일반물리학 실험 - 전류천칭 일반물리학 실험 - 운동량 보존
일반물리학 실험 - 운동량 보존

































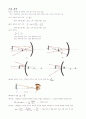














소개글