수압의 과도현상 . 예비레포트.

목차

1. 실험목적

2. 이 론
(1) 형상손실
figure1. 관수로의 형상에 의한 손실
(2) 유입에 의한 손실수두

3. 실험장치 및 시약

3. 실험방법

4. 참고문헌

5. 예상결과

6. 고 찰

본문내용

반경(m), S : 에너지 경사, C_HW : Hazen-Williams 계수로서 가장 매끈한 관에서는 150, 대단히 거치른 관에서는 80정도의 값을 가지며, 설계를 위한 평균치로는 100을 많이 사용한다.
Hazen-Williams식은 유도된 것이 아니라 "경험식"이다.
pipe에서 유동에 의한 마찰압력손실을 손쉽게 구하기 위해 넘어야 할 산은 friction factor(f) 값인데, Hazen-Williams식은 이 f값을 직접 사용하지 않고 경험적으로 정한 "C값"을 사용함으로써 "water line"에서의 압력 손실를 간단히 계산할 수 있게 한 것이다.
마찰력은 물 흐름의 반대로 가해지며 Hazen-Williams 공식을 사용하여, 우리는 아래와 같이 같이 이 마찰을 표현할수 있다.
= pipe diameter
= flow rate
= friction factor
좌측에서 우측으로 물이 이동하면 이 마찰력은 아래와 같이 정의 된다.
유량이 왼쪽에서 오른쪽으로 이동 할 때를 +방향이라고 한다면 (figure1), 이 항력은 아래와 같이 사용 할 수 있다.
at =density
g=gravity * density
a=area of pipe
A1 A2 = area of Tank
L=length of pipe
H1 H2= Height of tank
Q=flow rate of pipe
만약 유량의 방향이 변하면 역시 변하게 된다. 이 순힘은 두 가지 힘을 합하여야 함으로 순힘은 아래와 같다.
이 힘은 물탱크의 운동량을 변화시키므로 아래와 같다.
힘이 같아 질 때, 그 방정식은 파이프 안에서 물의 이동으로 나타난다.
이와 같은 방법을 아래와 같이 사용할 수 있다.
유량은 두 탱크의 높이 (, )에 의해 발생하며 나머지 시스템의 저장소 주변에 보존방정식을 찾을 수 있다.
탱크 1,
탱크 2,
이 세 가지 방정식은 하나의 간단한 모델에서 형성되었으며 많은 유사한 경우의 유용성 일반성을 따라 추론할 수 있다. 힘 균형의 방정식은 유량을 나타내고, 보존방정식은 축적을 나타내며, 여기에서 수압의 흐름이 발생한다. 이 개념은 Figure3으로 나타내었으며 상황에 따라 적용할 수 있다.
3. 실험장치 및 시약
3. 실험방법
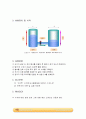
① 크기가 같은 두 개의 탱크를 연결한 후 벨브가 잠겨 있는지 확인한다.
② 탱크1의 수위가 30cm가 되도록 물을 채운다.
③ 벨브를 연후 시간에 따라 탱크 1의 수위를 기록한다.
④ 크기가 다른 탱크를 연결한 후 실험 2-3을 반복한다.
⑤ 길이가 다른 파이프를 연결한 후 실험 2-4를 반복한다.
4. 참고문헌
(1) "수리학" 신기화,도서출판일광,1995년, P.85~87
(2) 단위조작 이론 및 실험 프린트
5. 예상결과
각 수치에 대한 설정 값과 그에 따른 예상 그래프는 다음과 같다.
1)
: 0.5
: 0.5
: 1
: 0.5 (임의의 값)
: 0.5
2)
: 0.3
: 0.3
: 0.1
: 0.5 (임의의 값)
: 0.05
3)
: 0.2
: 0.2
: 10
: 0.001 (임의의 값)
: 1
각각의 변수를 임의로 정하여 시뮬레이션 해보고, 그래프의 유형에 따른 변화를 보기 위해 나머지 변수는 고정 시킨 후 파이프의 직경만을 변화시키면서 시뮬레이션 해 본 결과 직경이 작을수록 진동이 줄어드는 것을 알 수 있었다.
6. 고 찰
1. 실제 실험결과를 토대로 friction factor를 계산하시오.
2. 계산한 fraction factor을 이용하여 시뮬레이션 한 결과와 실제 결과의 차이에 대하여 서술하시오.
3. 실험에서 진동을 줄일 수 있는 방법에 대하여 서술하시오.
4. 시간에 따라 파이프의 유량 변화는 어떻게 될것인지 쓰시오.

키워드

수압,   과도현상,   손실수두