목차
1. 실험목표
2. 실험목적
3. 실험배경
-항력의 발생 이유와 원리
-거친 표면과 매끈한 표면을 가진 실린더 주변의 유동 차
-항력 계수 공식 유도
4. 실험결과
-매끈한 원통에서의 결과
-거친 원통에서의 결과
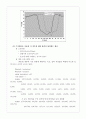
-두 경우의 위치에 따른 속도 분포 그래프
-수치 해석에 의한 각 경우의 항력계수값 계산
5.토론 주제
-입구 속도(15.072m/s)에 비해 wake region에서 벗어난 자유 유동속도가 왜 증가하였는지를 논하여라.
-매끈한 실린더와 거친 실린더의 속도 분포가 다르게 나타난다. 거친 경우의 최소 속도가 매끈한 경우보다 더 낮고 wake의 폭은 더 좁다. 그 이유를 논하여라.
2. 실험목적
3. 실험배경
-항력의 발생 이유와 원리
-거친 표면과 매끈한 표면을 가진 실린더 주변의 유동 차
-항력 계수 공식 유도
4. 실험결과
-매끈한 원통에서의 결과
-거친 원통에서의 결과
-두 경우의 위치에 따른 속도 분포 그래프
-수치 해석에 의한 각 경우의 항력계수값 계산
5.토론 주제
-입구 속도(15.072m/s)에 비해 wake region에서 벗어난 자유 유동속도가 왜 증가하였는지를 논하여라.
-매끈한 실린더와 거친 실린더의 속도 분포가 다르게 나타난다. 거친 경우의 최소 속도가 매끈한 경우보다 더 낮고 wake의 폭은 더 좁다. 그 이유를 논하여라.
본문내용
593,
13.593, 13.921, 14.102, 14.355, 14.407, 13.225, 8.769, 5.022, 3.741, 3.255,
2.658, 1.972, 1.651, 2.209, 2.832, 3.419, 4.871, 8.678, 13.071, 14.306, 14.311,
14.092, 14.092, 13.753, 13.753, 13.466, 13.466, 13.205, 13.205, 13.044};
// 속도 데이터를 구간 간격에 맞게 데이터를 늘려 정렬함
double p[]={99.230, 99.230, 100.928, 100.928, 103.435, 103.435, 105.753, 105.753,
109.760, 109.760, 115.114, 118.132, 122.407, 123.289, 103.887, 45.675,
14.983, 8.314, 6.294, 4.197, 2.310, 1.619, 2.897, 4.763, 6.945, 14.093,
44.731, 101.483, 121.568, 121.654, 117.963, 117.963, 112.358, 112.358,
107.708, 107.708, 103.579, 103.579, 101.066};
// 압력 데이터를 구간 간격에 맞게 데이터를 늘려 정렬함
double v_1[40],p_1[40]; // 데이터 보간을 위해 구간을 40개의 개별 단위로 나눔
double sum=0; // 중간 과정의 적분계산의 총합을 저장하는 변수
double integer=0, Cd=0; // 최종 적분값과 항력계수를 구하는 변수를 선언
double v_2; // 중간 계산을 위한 변수 선언
int i,j,k;
for(k=1; k<40; k++)
{ // 보간법을 위해 반복 루틴을 함.
for(i=1; i<40; i++) // 사다리꼴 수치적분법을 이용하여 적분수행
{
v1[i-1]=v[k-1]+(v[k]-v[k-1])/0.5/38*(0.5/38*i-0.5/38);
p1[i-1]=p[k-1]+(p[k]-p[k-1])/0.5/38*(0.5/38*i-0.5/38);
// 보간법에 의해 나누어진 데이터를 임시 배열에 저장
}
for(j=1; j<39; j++)
{
v_2=v1[j]+v1[j-1];
v_2=v_2/2;
sum=sum+0.5/38*pow(v_2,2);
}
}
integer=1/2*15.072^2*19;
integer=sum-integer;
integer=integer/100*0.000001241; // 변수 integer에 밀도를 포함한 최종값을 대입
cout << \"Fd=\" << integer << \"\\n\";
Cd=integer/19*100/0.000001241/pow(15.072,2)*2;
// 위에서 구해진 항력을 이용해 항력계수 계산
cout << \"Cd=\" << Cd << \"\\n\";
※ 계산결과 : 매끈한 원통의 경우.. Fd=0.000032, Cd=1.192952
거친 원통의 경우..... Fd=0.000031, Cd=1.157583
5. 고찰 및 토론
(1) 이론적으로 볼 때 입구쪽 유선에서 보다 실린더 양 옆쪽으로의 유선이 간격이 더 좁은 것을 확인할 수 있다. 동일한 유선 사이에 흐르는 유량은 같아야 하는데 이 경우 실린더 위아래의 유선의 폭이 좁기 때문에 같은 질량의 유체가 흐르면서 속도가 더 빨라지는 것이다. 또한 박리영역 앞쪽에는 압력 구배가 음수가 되고 뒤쪽에서는 양수가 된다. 베르누이 정리에 의하면 속도와 압력은 반비례 관계를 갖는다. 그렇기 때문에 박리영역 뒤쪽에서 나타나는 wake region에서는 속도는 느려지고 압력은 높아진다. 하지만 wake region을 벗어난 자유 유동장에서는 wake region보다 압력이 낮기 때문에 속도가 상대적으로 증가한 것이다.
(2) 매끈한 원통의 유동이 거친 원통의 유동보다 박리점을 앞쪽으로 이동시킨다. 즉, 층류 경계층의 경우는 박리가 원통 전반부에 발생하기 때문에 후류역에 인접한 자유유동에서 유선이 점진적으로 좁아진다. 이것은 연속방정식으로부터 속도의 증가를 의미하기 때문에 결국 압력감소로 나타난다. 반면에 난류 경계층의 경우는 박리점이 하류로 천이되기 때문에 후류역에 인접한 자유유동에서 유선의 확대부가 생긴다. 이 확대부에서 확산 때문에 속도가 감속되고, 베르누이 정리에 의하여 이 감속은 결국 압력 증가로 나타난다. 이러한 이유에서 박리역의 배압은 난류경계층 유동의 경우가 층류경계층 유동의 경우보다 높고 속도는 낮게 된다.
13.593, 13.921, 14.102, 14.355, 14.407, 13.225, 8.769, 5.022, 3.741, 3.255,
2.658, 1.972, 1.651, 2.209, 2.832, 3.419, 4.871, 8.678, 13.071, 14.306, 14.311,
14.092, 14.092, 13.753, 13.753, 13.466, 13.466, 13.205, 13.205, 13.044};
// 속도 데이터를 구간 간격에 맞게 데이터를 늘려 정렬함
double p[]={99.230, 99.230, 100.928, 100.928, 103.435, 103.435, 105.753, 105.753,
109.760, 109.760, 115.114, 118.132, 122.407, 123.289, 103.887, 45.675,
14.983, 8.314, 6.294, 4.197, 2.310, 1.619, 2.897, 4.763, 6.945, 14.093,
44.731, 101.483, 121.568, 121.654, 117.963, 117.963, 112.358, 112.358,
107.708, 107.708, 103.579, 103.579, 101.066};
// 압력 데이터를 구간 간격에 맞게 데이터를 늘려 정렬함
double v_1[40],p_1[40]; // 데이터 보간을 위해 구간을 40개의 개별 단위로 나눔
double sum=0; // 중간 과정의 적분계산의 총합을 저장하는 변수
double integer=0, Cd=0; // 최종 적분값과 항력계수를 구하는 변수를 선언
double v_2; // 중간 계산을 위한 변수 선언
int i,j,k;
for(k=1; k<40; k++)
{ // 보간법을 위해 반복 루틴을 함.
for(i=1; i<40; i++) // 사다리꼴 수치적분법을 이용하여 적분수행
{
v1[i-1]=v[k-1]+(v[k]-v[k-1])/0.5/38*(0.5/38*i-0.5/38);
p1[i-1]=p[k-1]+(p[k]-p[k-1])/0.5/38*(0.5/38*i-0.5/38);
// 보간법에 의해 나누어진 데이터를 임시 배열에 저장
}
for(j=1; j<39; j++)
{
v_2=v1[j]+v1[j-1];
v_2=v_2/2;
sum=sum+0.5/38*pow(v_2,2);
}
}
integer=1/2*15.072^2*19;
integer=sum-integer;
integer=integer/100*0.000001241; // 변수 integer에 밀도를 포함한 최종값을 대입
cout << \"Fd=\" << integer << \"\\n\";
Cd=integer/19*100/0.000001241/pow(15.072,2)*2;
// 위에서 구해진 항력을 이용해 항력계수 계산
cout << \"Cd=\" << Cd << \"\\n\";
※ 계산결과 : 매끈한 원통의 경우.. Fd=0.000032, Cd=1.192952
거친 원통의 경우..... Fd=0.000031, Cd=1.157583
5. 고찰 및 토론
(1) 이론적으로 볼 때 입구쪽 유선에서 보다 실린더 양 옆쪽으로의 유선이 간격이 더 좁은 것을 확인할 수 있다. 동일한 유선 사이에 흐르는 유량은 같아야 하는데 이 경우 실린더 위아래의 유선의 폭이 좁기 때문에 같은 질량의 유체가 흐르면서 속도가 더 빨라지는 것이다. 또한 박리영역 앞쪽에는 압력 구배가 음수가 되고 뒤쪽에서는 양수가 된다. 베르누이 정리에 의하면 속도와 압력은 반비례 관계를 갖는다. 그렇기 때문에 박리영역 뒤쪽에서 나타나는 wake region에서는 속도는 느려지고 압력은 높아진다. 하지만 wake region을 벗어난 자유 유동장에서는 wake region보다 압력이 낮기 때문에 속도가 상대적으로 증가한 것이다.
(2) 매끈한 원통의 유동이 거친 원통의 유동보다 박리점을 앞쪽으로 이동시킨다. 즉, 층류 경계층의 경우는 박리가 원통 전반부에 발생하기 때문에 후류역에 인접한 자유유동에서 유선이 점진적으로 좁아진다. 이것은 연속방정식으로부터 속도의 증가를 의미하기 때문에 결국 압력감소로 나타난다. 반면에 난류 경계층의 경우는 박리점이 하류로 천이되기 때문에 후류역에 인접한 자유유동에서 유선의 확대부가 생긴다. 이 확대부에서 확산 때문에 속도가 감속되고, 베르누이 정리에 의하여 이 감속은 결국 압력 증가로 나타난다. 이러한 이유에서 박리역의 배압은 난류경계층 유동의 경우가 층류경계층 유동의 경우보다 높고 속도는 낮게 된다.
추천자료
 빛의 속도(광속)측정 방법과 지구-태양-달의 크기,거리 측정방법
빛의 속도(광속)측정 방법과 지구-태양-달의 크기,거리 측정방법 보의 굽힘 - 보의 휨 모멘트 측정, 하중이 부하된 점에서 떨어진 점의 모멘트, 단순지지 보의...
보의 굽힘 - 보의 휨 모멘트 측정, 하중이 부하된 점에서 떨어진 점의 모멘트, 단순지지 보의... [물리실험 보고서] 쇠구슬의 밀도 측정 : 쇠구슬의 크기에 따른 질량을 측정하여 거듭제곱법...
[물리실험 보고서] 쇠구슬의 밀도 측정 : 쇠구슬의 크기에 따른 질량을 측정하여 거듭제곱법... COD(화학적 산소 소비량) 측정 : COD(화학적산소소비량)은 물의 오염도를 나타내는 지표의 하...
COD(화학적 산소 소비량) 측정 : COD(화학적산소소비량)은 물의 오염도를 나타내는 지표의 하... [공학] 아르키메데스 법을 이용한 밀도 측정 : 아르키메데스 법을 이용하여 소결된 ZnO의 밀...
[공학] 아르키메데스 법을 이용한 밀도 측정 : 아르키메데스 법을 이용하여 소결된 ZnO의 밀... [화공 기초 실험] 과산화수소의 농도 측정 [예비] : 습식정량분석법 중의 하나인 적정법을 사...
[화공 기초 실험] 과산화수소의 농도 측정 [예비] : 습식정량분석법 중의 하나인 적정법을 사... 물리 실험 - 길이 및 곡률반경 측정 & 구면의 곡률 반지름 측정
물리 실험 - 길이 및 곡률반경 측정 & 구면의 곡률 반지름 측정 방사선계측실험 (결과) - 베타선 최대에너지 측정 (베타선 최대에너지 측정)
방사선계측실험 (결과) - 베타선 최대에너지 측정 (베타선 최대에너지 측정) 방사선계측실험 (결과) - GM계측기의 방사능 측정효율 측정
방사선계측실험 (결과) - GM계측기의 방사능 측정효율 측정 [화학1실험/아주대] 질량부피 및 온도측정 (A+) : 질량 부피 온도 등을 측정해 보고, 정확도...
[화학1실험/아주대] 질량부피 및 온도측정 (A+) : 질량 부피 온도 등을 측정해 보고, 정확도... [물리학 실험] 보다진자를 이용한 중력가속도 측정 : Borda의 진자를 이용하여 그 지점의 중...
[물리학 실험] 보다진자를 이용한 중력가속도 측정 : Borda의 진자를 이용하여 그 지점의 중... [일반물리학 실험] 구심력 측정 : 물체가 일정한 각속도로 원운동을 할 때 그 구심력을 측정...
[일반물리학 실험] 구심력 측정 : 물체가 일정한 각속도로 원운동을 할 때 그 구심력을 측정... [일반물리학 실험] 마찰계수 측정 : 두 물체의 표면 사이에 작용하는 운동마찰계수와 정지마...
[일반물리학 실험] 마찰계수 측정 : 두 물체의 표면 사이에 작용하는 운동마찰계수와 정지마... [일반물리학 실험] 중력가속도 측정 : 보다(Borda) 진자의 주기와 길이를 측정하여 그 지점의...
[일반물리학 실험] 중력가속도 측정 : 보다(Borda) 진자의 주기와 길이를 측정하여 그 지점의...





























소개글