
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
-
11
-
12
-
13
-
14
-
15
-
16
-
17
-
18
-
19
-
20
-
21
-
22
-
23
-
24
-
25
-
26
-
27
-
28
-
29
-
30
-
31
-
32
-
33
-
34
-
35
-
36
-
37
-
38
-
39
-
40
-
41
-
42
-
43


본문내용
해법
2) 단위당 공헌율
50 ≤ ≤ 133.33
45 ≤ ≤ 120
3) 두 번째 제약조건의 우변상수값이 12에서 10으로 감소했을 경우
의 범위는 9 ≤ 12 ≤ 19.174 이므로 12에서 10으로 감소해도 최적해는 변화없다.
4) 세 번째 제약조건의 우변상수값이 10에서 9로 감소했을 경우
의 범위는 No Limit ≤ 10 ≤ 13.6 이므로 10에서 9로 감소해도 최적해는 변화없다.
6.
1) A=0, B=10, C=20, 총이익 Z= 260,000
2) 전나무의 그림자 가격 = 0원, 90 ≤
3) 한계가치 : 2,000원, 20 ≤ ≤ 80
4) 절단과 압축 두 공정의 가용시간을 늘릴 수 있다.
→ 두 공정의 그림자가격이 2000원으로 같기 때문에 가용시간이 늘어나면 총이익도 같이 증가하기 때문이다.
5) 전나무가 160에서 100으로 줄어도 최적해는 변화없다.
→ 90 ≤ 에서 최적해를 유지하기 때문이다.
6) 제품 A의 단위당 이익은 2000원이 증가해야 한다.
7) 제품 C의 단위당 이익은 8000에서 13000으로 증가한다면 최적해가 변하지 않는다.
→ 5000 ≤ ≤ 20000의 범위이기 때문이다.
8) 합판D를 추가로 생산한다고 하더라도 최적해는 변화없다.
최대화 Z=4,000+10,000+8,000+6,000
제약조건 5+4+4+3≤200
2+5+2+4≤160
++2+≤50
2+4+2+4≤80
,, , ≥0
7.
1) 174.5만큼 증가하여야 한다.
2) 의 단위당 공헌율이 75로 변화하여도 최적해는 변함이 없다.
→ 0≤ 이기 때문이다.
3)
을 변경할 수 있는 범위 : 0 ≤ ≤ 50
를 변경할 수 있는 범위 : 20 ≤
를 변경할 수 있는 범위 : 0 ≤
를 변경할 수 있는 범위 : 0 ≤
4) 2 + + 10와 제약조건 추가로 인한 최적해의 변화
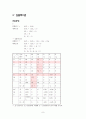
Final Optimal Solution
Z = 3125.000
----------------------------------------
Variable Value Reduced Cost
----------------------------------------
X1 0.000 174.500
X2 20.000 0.000
X3 8.000 0.000
X4 11.000 0.000
----------------------------------------
Constraint Slack/Surplus Shadow Price
----------------------------------------
C1 0.000 45.000
C2 5.000 0.000
C3 0.000 7.200
C4 0.000 27.500
C5 103.000 0.000
----------------------------------------
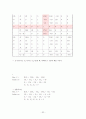
Objective Coefficient Ranges
-----------------------------------------------------------------------
Lower Current Upper Allowable Allowable
Variables Limit Values Limit Increase Decrease
-----------------------------------------------------------------------
X1 No limit 60.000 234.500 174.500 No limit
X2 0.000 90.000 No limit No limit 90.000
X3 0.000 90.000 No limit No limit 90.000
X4 0.000 55.000 No limit No limit 55.000
--------------------------------------------------------------------
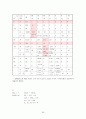
Right Hand Side Ranges
-----------------------------------------------------------------------
Lower Current Upper Allowable Allowable
Constraints Limit Values Limit Increase Decrease
-----------------------------------------------------------------------
C1 0.000 40.000 50.000 10.000 40.000
C2 20.000 25.000 No limit No limit 5.000
C3 0.000 100.000 No limit No limit 100.000
C4 1.400 22.000 No limit No limit 20.600
C5 No limit 55.000 158.000 103.000 No limit
--------------------------------------------------------------------
***** End of Output *****
⇒ 결과적으로 새로운 제약조건을 추가하여도 최적해에는 변함이 없다.
5) 3690.71으로 기존의 최적해 3125보다는 커진다.
Ⅵ 정수 및 0-1 계획법
[연습문제]
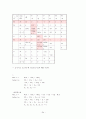
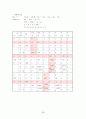
8.
번호
실행가능성검토
목적함수값
제약조건1
제약조건2
1
0
0
0
실행불가능
-
-
2
0
0
1
실행불가능
-
-
3
0
1
0
실행불가능
-
-
4
0
1
1
실행가능
실행가능
6
5
1
0
0
실행가능
실행불가능
-
6
1
0
1
실행가능
실행가능
7
7
1
1
0
실행가능
실행가능
5
8
1
1
1
실행가능
실행가능
9
⇒ =1이고 =1이고 =0일 경우 최소값 5를 가진다.
9.
최대화 Z=300 + 440 + 60 + 160 + 380 + 200
제약조건700 + 1080 + 120 + 300 + 680 + 420 ≤ 2000
6 + 16 + 2 + 4 + 10 + 6 ≤ 24
200 + 300 + 20 + 70 + 150 + 90 ≥ 200
160 + 240 + 36 + 66 + 140 + 80 ≥ 200
+ = 1
- = 0
Xi = 0 or 1 (i = 1, 2, 3, 4, 5, 6)
10.
⇒ =0이고 =4일 때, 64000의 해를 갖는다.
2) 단위당 공헌율
50 ≤ ≤ 133.33
45 ≤ ≤ 120
3) 두 번째 제약조건의 우변상수값이 12에서 10으로 감소했을 경우
의 범위는 9 ≤ 12 ≤ 19.174 이므로 12에서 10으로 감소해도 최적해는 변화없다.
4) 세 번째 제약조건의 우변상수값이 10에서 9로 감소했을 경우
의 범위는 No Limit ≤ 10 ≤ 13.6 이므로 10에서 9로 감소해도 최적해는 변화없다.
6.
1) A=0, B=10, C=20, 총이익 Z= 260,000
2) 전나무의 그림자 가격 = 0원, 90 ≤
3) 한계가치 : 2,000원, 20 ≤ ≤ 80
4) 절단과 압축 두 공정의 가용시간을 늘릴 수 있다.
→ 두 공정의 그림자가격이 2000원으로 같기 때문에 가용시간이 늘어나면 총이익도 같이 증가하기 때문이다.
5) 전나무가 160에서 100으로 줄어도 최적해는 변화없다.
→ 90 ≤ 에서 최적해를 유지하기 때문이다.
6) 제품 A의 단위당 이익은 2000원이 증가해야 한다.
7) 제품 C의 단위당 이익은 8000에서 13000으로 증가한다면 최적해가 변하지 않는다.
→ 5000 ≤ ≤ 20000의 범위이기 때문이다.
8) 합판D를 추가로 생산한다고 하더라도 최적해는 변화없다.
최대화 Z=4,000+10,000+8,000+6,000
제약조건 5+4+4+3≤200
2+5+2+4≤160
++2+≤50
2+4+2+4≤80
,, , ≥0
7.
1) 174.5만큼 증가하여야 한다.
2) 의 단위당 공헌율이 75로 변화하여도 최적해는 변함이 없다.
→ 0≤ 이기 때문이다.
3)
을 변경할 수 있는 범위 : 0 ≤ ≤ 50
를 변경할 수 있는 범위 : 20 ≤
를 변경할 수 있는 범위 : 0 ≤
를 변경할 수 있는 범위 : 0 ≤
4) 2 + + 10와 제약조건 추가로 인한 최적해의 변화
Final Optimal Solution
Z = 3125.000
----------------------------------------
Variable Value Reduced Cost
----------------------------------------
X1 0.000 174.500
X2 20.000 0.000
X3 8.000 0.000
X4 11.000 0.000
----------------------------------------
Constraint Slack/Surplus Shadow Price
----------------------------------------
C1 0.000 45.000
C2 5.000 0.000
C3 0.000 7.200
C4 0.000 27.500
C5 103.000 0.000
----------------------------------------
Objective Coefficient Ranges
-----------------------------------------------------------------------
Lower Current Upper Allowable Allowable
Variables Limit Values Limit Increase Decrease
-----------------------------------------------------------------------
X1 No limit 60.000 234.500 174.500 No limit
X2 0.000 90.000 No limit No limit 90.000
X3 0.000 90.000 No limit No limit 90.000
X4 0.000 55.000 No limit No limit 55.000
--------------------------------------------------------------------
Right Hand Side Ranges
-----------------------------------------------------------------------
Lower Current Upper Allowable Allowable
Constraints Limit Values Limit Increase Decrease
-----------------------------------------------------------------------
C1 0.000 40.000 50.000 10.000 40.000
C2 20.000 25.000 No limit No limit 5.000
C3 0.000 100.000 No limit No limit 100.000
C4 1.400 22.000 No limit No limit 20.600
C5 No limit 55.000 158.000 103.000 No limit
--------------------------------------------------------------------
***** End of Output *****
⇒ 결과적으로 새로운 제약조건을 추가하여도 최적해에는 변함이 없다.
5) 3690.71으로 기존의 최적해 3125보다는 커진다.
Ⅵ 정수 및 0-1 계획법
[연습문제]
8.
번호
실행가능성검토
목적함수값
제약조건1
제약조건2
1
0
0
0
실행불가능
-
-
2
0
0
1
실행불가능
-
-
3
0
1
0
실행불가능
-
-
4
0
1
1
실행가능
실행가능
6
5
1
0
0
실행가능
실행불가능
-
6
1
0
1
실행가능
실행가능
7
7
1
1
0
실행가능
실행가능
5
8
1
1
1
실행가능
실행가능
9
⇒ =1이고 =1이고 =0일 경우 최소값 5를 가진다.
9.
최대화 Z=300 + 440 + 60 + 160 + 380 + 200
제약조건700 + 1080 + 120 + 300 + 680 + 420 ≤ 2000
6 + 16 + 2 + 4 + 10 + 6 ≤ 24
200 + 300 + 20 + 70 + 150 + 90 ≥ 200
160 + 240 + 36 + 66 + 140 + 80 ≥ 200
+ = 1
- = 0
Xi = 0 or 1 (i = 1, 2, 3, 4, 5, 6)
10.
⇒ =0이고 =4일 때, 64000의 해를 갖는다.
추천자료
 2007년 2학기 패션마케팅 중간시험과제물 A형(패션브랜드비교)
2007년 2학기 패션마케팅 중간시험과제물 A형(패션브랜드비교) 2011년 1학기 시뮬레이션 중간시험과제물 E형(대기시간)
2011년 1학기 시뮬레이션 중간시험과제물 E형(대기시간) [취업과 자기계발 중간고사] 직무스트레스(job stress)에 대하여
[취업과 자기계발 중간고사] 직무스트레스(job stress)에 대하여 2013년 1학기 동서양고전의이해 중간시험과제물 C형(메논을 읽고)
2013년 1학기 동서양고전의이해 중간시험과제물 C형(메논을 읽고) 2014년 1학기 인터넷서비스 중간시험과제물 공통(인터넷통신과정, 청소년폭력사이트접속문제)
2014년 1학기 인터넷서비스 중간시험과제물 공통(인터넷통신과정, 청소년폭력사이트접속문제) 2018년 1학기 식품미생물학 중간시험과제물 공통(미생물의 생육에 영향을 미치는 내적외적)
2018년 1학기 식품미생물학 중간시험과제물 공통(미생물의 생육에 영향을 미치는 내적외적) 2018년 1학기 급식경영학 중간시험과제물 공통(4차 산업혁명이 외식산업에 주는 영향)
2018년 1학기 급식경영학 중간시험과제물 공통(4차 산업혁명이 외식산업에 주는 영향) 2018년 1학기 유아건강교육 중간시험과제물 A형(만 0~1세, 2세 표준보육과정)
2018년 1학기 유아건강교육 중간시험과제물 A형(만 0~1세, 2세 표준보육과정) 2018년 1학기 유아건강교육 중간시험과제물 B형(만 3, 4, 5세 누리과정)
2018년 1학기 유아건강교육 중간시험과제물 B형(만 3, 4, 5세 누리과정) 2018년 1학기 정보통신망 중간시험과제물 A형(Connected car)
2018년 1학기 정보통신망 중간시험과제물 A형(Connected car) 2018년 1학기 정보통신망 중간시험과제물 B형(Digital Healthcare)
2018년 1학기 정보통신망 중간시험과제물 B형(Digital Healthcare) 2018년 1학기 정보통신망 중간시험과제물 C형(Drone)
2018년 1학기 정보통신망 중간시험과제물 C형(Drone) 2018년 1학기 정보통신망 중간시험과제물 D형(Internet of Things)
2018년 1학기 정보통신망 중간시험과제물 D형(Internet of Things) 2018년 1학기 정보통신망 중간시험과제물 E형(Block chain)
2018년 1학기 정보통신망 중간시험과제물 E형(Block chain)
























































소개글