기계공학실험 진동실험-1자유도 진동계의 자유진동 실험레포트

소개글

기계공학실험 진동실험-1자유도 진동계의 자유진동 실험레포트 에 대한 보고서 자료입니다.

본문내용

영역 Data에서 logarithmic decrement δ를 구하여 감쇠율 와 감쇠계수 을 구한다. : 원래는 변위 그래프에서 δ를 구하지만 여기서는 가속도 데이터를 가지고 구함.
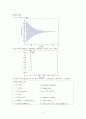
5. 주파수 영역 Graph에서 구한 감쇠 고유주파수 와 앞에서 구한 감쇠율 를 사용하여 spring상수 값을 으로부터 구함.
*2번에서 구한 k값 466.95 와 비교해 볼 때 감쇠를 고려한 값이 약간 더 크게 나왔지만 거의 차이가 나지 않는다. 이것은 스프링 자체의 감쇠가 매우 약하다는 것을 뜻한다.
5. Spring의 재질 : 다음의 스프링 상수의 정의를 이용해서 전단응력계수 G를 구해서 스프링의 재질을 예측한다.
이 값은 steel의 전단응력계수보다 알루미늄의 전단응력계수 에 가까운 값이므로 스프링의 재질은 알루미늄이라고 할 수 있다.
4. 결론 및 토의
이론값에 비해 스프링 상수가 약 25%정도 부족한 값이 나왔다. 이는 1자유도 진동으로 가정한 실험이지만 실제로 스프링이 자유롭게 움직이므로 3자유도라고 할 수 있고, 가속도계와 연결선의 무게를 고려하지 않은 점도 오차요인이 될 수 있다.
그리고 매트랩에서 FFT 함수를 이용해서 시스템의 주파수를 구하였는데, 이에 대한 것을 정확히 알지 못해서 여기에서 실수나 오류가 있을 수 도 있을 것이다.
또한 스프링의 전단응력계수도 가공할 때 받는 에너지나 내부미세구조의 변형등으로 인해 이론적인 값과 차이가 있을 수도 있을 것이다.
-참고 문헌-
Engineering Vibration 2nd Edition , Daniel J. Inman , Prentice Hall , 2001

키워드

진동실험,   1자유도,   스프링,   진동,   기계공학실험,   비감쇠