에어백 회로 설계

목차

□ 서 론

□ 설 계 수 행
- 상황정의 및 가정 설정
- 설계 목표 정의
- 계획 수립
- 계획 수행
- 결과의 검증 순서로 작성

□ 결 론

□ 설 계 소 감

본문내용

4-3-2에서 볼 수 있는 것처럼 저
항R에서 발산하는 에너지가 1[J]이 되지 않기 때문에 임계제동시에는 자동차 에어백 설계를 할 수 없다.
3. 설 계 수 행
4-4. 부족제동(underdamp) - < 일 때 두 복소수
앞에서 본 바와 같이 자연응답에서 이다. 여기서 두 근은 < 일 때 이 된다.
라 정의 하면 이고
자연응답은 이다.
오일러 공식을 이용해서 식을 간단히 하면
계수 는 미정이므로 라고 놓으면
(4-4-1) 이 된다.
이러한 자연응답은 < 일 때 < 즉, < 인 경우에
얻을 수 있다.
신속한 응답을 얻기 위해서 로 가정을 하면,
이고, Ω 이므로 이고,
이다.
이므로 이다.
이므로
자연응답 식(4-4-1)을 이용하면
(4-4-2) 가 된다.
= 이고
가 된다.
이다.
3. 설 계 수 행
4-5. 축전지 전압의 최소전압을 고려하였을 경우
초기전압 이라 가정하고 자연응답 식(4-4-1)을 이용하면
(4-5-1) 가 된다.
= 이므로
가 된다.
이다.
그림 4-5-1
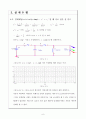
그림 4-5-1은 축전지의 최소전압을 고려하여 최소 전압이 11.6V일 때 회로 구성도이다.
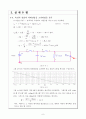
그림 4-5-2
그림 4-5-2를 통해서 저항 R에서 발산하는 에너지를 나타내었다. 그래프를 보면 t=0ms 일 때 22.42 에서 t=90ms일 때 0 까지 거의 선형적으로 감소 하고 있음을 알 수 있다. 그러므로 처음 100ms동안 저항에서 발산하는 에너지는
이다. 따라서 1 J 이상의 에너지를 발산함으로 0.1초 내에서 자동차 에어백은 정상 적으로 작동 할 것이다.
3. 설 계 수 행
4-6. 축전지 전압의 최대전압을 고려하였을 경우
초기전압 이라 가정하고 자연응답 식(4-4-1)을 이용하면
(4-6-1) 가 된다.
= V 이므로
가 된다.
이다.
그림 4-6-1
그림 4-6-1은 축전지의 최대전압을 고려하여 최소 전압이 15V일 때 회로 구성도이다.
그림 4-6-2
그림 4-6-2를 통해서 저항 R에서 발산하는 에너지를 나타내었다. 그래프를 보면 t=0ms 일 때 37.5 에서 t=90ms일 때 0 까지 거의 선형적으로 감소 하고 있음을 알 수 있다. 그러므로 처음 100ms동안 저항에서 발산하는 에너지는
이다. 따라서 1 J 이상의 에너지를 발산함으로 0.1초 내에서 자동차 에어백은 정상 적으로 작동 할 것이다.
3. 설 계 수 행
4-7. 가격대비를 고려한 L과 C를 선정 후 설계.
설계과정에서 가격대비를 고려하였을 경우 최소의 비용으로 설계를 해야하기 때문에 최소의 비용을 고려한다면 변경할 수 있는 수동소자를 최소의 가격으로 설정 해야 할 것이다. 우선 커패시터의 경우부터 살펴 보면 커패시터의 가격은 그 용량에 비례한 다. 따라서 적은 용량의 커패시터를 우선 택하여야 할 것이다. 이기 때문 에 C값이 적어짐에 따라 의 값이 커질 것이다.
이고 < 이므로 < 246.7 이다.
C > 5.3mF 이다. 만약 C = 6mF으로 가정 한다면
이고, 이다.
이므로
이고 = 이므로
가 된다
이다.
3. 설 계 수 행
(5) 결과의 검증
5-1 신속한 응답을 위해 = 2 로 선택한 경우.
그림 5-1-1
앞의 결과를 토대로 그림 8-1과 같이 회로도 구성 후 pspice를 이용한 simuration.
그림 8-2
그림 8-2를 통해서 저항 R에서 발산하는 에너지를 나타내었다. 그래프를 보면 t=0ms 일 때 24 에서 t=90ms일 때 0 까지 거의 선형적으로 감소 하고 있음을 알 수 있다. 그러므로 처음 100ms동안 저항에서 발산하는 에너지는
이다. 따라서 1 J 이상의 에너지를 발산함으로 0.1초 내에서 자동차 에어백은 정상 적으로 작동 할 것이다.
3. 설 계 수 행
5 - 2 가격대비를 고려하여 L과 C값을 선택한 경우.
그림 5-2-1
위의 결과를 토대로 그림 5-2-1과 같이 회로도 구성 후 pspice를 이용한 simuration.
그림 5-2-2
그림 5-2-2를 통해서 저항 R에서 발산하는 에너지를 나타내었다. 그래프를 보면 t=0ms 일 때 24 에서 t=90ms일 때 0 까지 거의 선형적으로 감소 하고 있음을 알 수 있다. 그러므로 처음 100ms동안 저항에서 발산하는 에너지는
이다. 따라서 1 J 이상의 에너지를 발산함으로 0.1초 내에서 자동차 에어백은 정상 적으로 작동 할 것이다.
4. 결 론
설계 수행을 하면서 생각되는 문제점은 가격대비를 고려하였을 경우에 인덕턴스(L)과 커패시터(C)값을 선택하려고 하였을 때 커패시터(C)의 가격은 용량과 비례하기 때문에 최소한으로 적은 값으로 결정 해주기 위해서 커패시터(C)의 용량을 최소화 하였고 그 커패시터에 맞게 인덕턴스(L)의 값도 결정해 주었다.
그리고 그림 5-2-1과 같이 회로도를 구성하고 simulation을 하였을 경우 R에서 발산하는 에너지의 출력파형 그래프는 그림 5-1-1의 회로처럼 =2로 가정하고 회로를 구성하였을 경우와는 다르게 그림 5-2-2의 출력파형은 선형적이지가 못하였다.
결국 선형적이지 못하면 거기에서 일은 1J이 되지 못 할 것이라 생각이 든다.
그래서 커패시터(C)의 용량을 올리면서 그에 따른 인덕턴스(L)의 값을 정해 simulation을 하였지만 마찬가지 였고 결국 그림 5-1-1의 회로처럼 =2로 가정하고 회로를 구성하였을 때가 최상의 조건을 만족 하였다.
5. 설 계 소 감
설계라는 것을 처음으로 접하였다. 처음에는 정말 막막하고 어떻게 해야할지 갈피를 못잡고 있었지만 조금씩 하다가 보니 자신감도 생기고 이렇게 마무리를 지으면서 느끼는 이 뿌듯함은 마치 머리 싸메고 풀었던 수학문제 한문제처럼 어디에 견주어도 못 할 것 이다.
그러나 이러한 뿌듯함이 크기는 하지만 앞으로 더욱더 열심히 해야 하겠다는 심정이 더 앞서는거 같다. 이번에 설계를 하면서 많이 모자랐던 OrCad 및 Matlab 등의 꼭 필요한 프로그램들의 중요성을 새삼스럽게 또 한번 느꼈고 더욱 열심히 해야 겠다는 생각에 여념이 없다.
앞으로 설계라는 것이 몸에 익을 수 있을 때 까지... 여러 프로그램들을 능숙히 다룰 수 있을 때까지... 무한히 연습하고 노력해야 할 것 같다.

키워드

에어백,   회로,   설계