베르누이 방정식과 유체 영동

소개글

베르누이 방정식과 유체 영동에 대한 보고서 자료입니다.

목차

1. 실험목적

2. 이 론

3. 실험 장치 및 기기

4. 실험data / 토의

5. 결 론

6. 참고 문헌

본문내용

viscous, along a streamline 의 조건을 만족해야 한다. 하지만 실제 실험에서 Flow가 흐르는 동안 단면적의 변화와 속도의 증가에 따른Unsteady-state의 유동이 발생 할 수 있으며 특히 최대 유동 속력을 갖게 되는 지점이후에 영향을 미쳤을 것이다. 또한, 노즐의 면적이 좁아지면 속도가 증가하는 것을 (이것은 베르누이 방정식에서도 알 수 있는 사실) 즉, 전압과 정압의 차이가 증가할수록 속도가 증가함을 알 수 있었는데 이것은 각 위치에서의 속도가 압력과 반비례적인 관계에 있다는 사실을 보였다 또한 사용된 유체인 Water의 경우도 엄밀히 incompressible의 물질이 아니며, Flow가 Channel cross-sectional Area를 지나면서 벽면과의 마찰로 인한 에너지 손실로 이론상의 Bernoullis Theorem과의 차이인 Head Loss를 만들었다고 판단된다. 실험적인 측면에서는 Section 1-3번까지의 유체의 유동은 Tube의 단면적이 작아지면서 압력이 큰 쪽에서 압력이 작아지는 방향으로의 흐름이 형성된 것으로 Steady State를 유지하는데 무리가 없었지만 Section 4-6번의 유동은 Tube의 면적이 다시 커지면서 압력이 작은 상태에서 큰 상태로 진행됨에 따라 유체의 유동방향의 반대의 흐름을 유발할 수 있다. 이러한 요인이 Stead State를 이루는데 방해 요소가 되어 실험값의 오차를 만들어 낼 수 있다. 또한 유체의 유동 중 받게 되는 Shear forced와 Viscosity의 관계는 의 관계를 가지기 때문에 Water를 Newtonian Fluid로 생각하면 유체의 유동속도가 커질수록 벽면과의 Shear Force가 커지게 되며 유체의 유동을 방해하는 더 큰 마찰력으로 작용 한다. 그리고 유동 속력이 커지게 되면 그에 따라 Turbulent가 발생하는데 Turbulent에 의해 잃는 에너지 손실도 속력이 증가함에 따른 더 큰 Head Loss 만들어냈다고 생각한다. 유체의 마찰손실(friction loss) 현상은 유체가 관내를 흐를 때 관로 면에 닿는 유체의 분자는 유체상호간, 유체와 내벽간의 마찰로 인하여 유체가 갖는 에너지의 일부가 손실되는 현상을 말하는데 Darcy-Weisbach Equation에 의하면 원형관의 마찰손실수두는 아래 식과 같다
Darcy-Weisbach Equation
f : 마찰계수(Friction Factor),
d : 관내경(m),
l : 관길이(m),
: 유속(m/s)
마찰계수는 유체가 유동하는 동안에 유체입자들의 운동은 점성의 영향으로 서로 다른 입자들의 운동을 감속시키거나 가속시키는 결과를 가져오는데 이로 인한 유동은 층류가 되거나 난류가 되는 데 이것을 구분하는데 사용되는 Re(Reynolds)수에 의하여 정하여 지는데, 층류에서의 마찰계수 f 는 관내면의 거칠기와 상관없이 아래 식과 같다.
Pipe flow의 Entrance Length에 영향을 미치는 parameterEntrance length는 관내 유동에서 입구에서부터 완전히 발달된 유동(fully developed flow)이 시작되는 지점까지의 길이를 나타내는 것으로 이 Entrance length는 그 유동상태가 층류인가 난류인가에 따라서 달라지는데
a) 층류에서의 Entrance length
b) 난류에서의 Entrance length
위와 같이 Entrance length는 관의 직경에 비례하며 Reynolds Number의 지수형태로 비례한다. Reynolds Number는 로 정의됨에 따라 Entrance length도 유체의 밀도 및 유동속도 관의 직경에 비례하며 Viscosity에 반비례하는 값의 가지므로 이에 따라 Entrance length도 위의 유체의 밀도 및 유동속도, 관의 직경과 Viscosity에 영향을 받게 된다
라. 오차 원인 및 개선 사항
- 이번 실험을 하면서 가장 아쉬웠던 점은 Bernoullis Theorem은 viscosity가 없는 유체로 가정하였으나 이를 증명하기 위한 실제 실험에서 사용된 water가 viscosity를 가지고 있기 때문에 Tube안을 흐르면서 벽면과의 마찰을 일으키고 에너지 손실을 가져왔다는 것이다. 이 현상은 유관의 뒤쪽으로 갈수록 그 정도가 누적되기 때문에 뒤쪽으로 가면서 얻은 Head Loss가 더 부정확한 값을 가졌다고 생각할 수 있다. 따라서 viscosity에 따른 Tube에서의 효과를 고려하기 위해 단면적의 변화 없이 Section별 Head Loss를 측정하여 관의 길이 변화에 따른 영향을 보정하여 계산하면 더욱 정확한 값을 가졌을 것이다. 이번실험은하나의 Tube안에서 단면적을 변화시키며 실험을 한 것보다 단면적이 다른 단일 Tube로 교체하면서 실험값을 측정하였다면 Stead State를 유지하여 유체의 속력 변화에 따른 다른 부수적인 효과나 역 압력이 생기는 것을 방지 할 수 있었을 것이다. 또한 이러한 여건이 갖추어지지 않았을 경우는 속도의 변화에 따른 Turbulent의 효과 등이 나타나는지 확인하기 위하여 Tube에 염료나 수소기체 등을 이용하여 지나는 유체의 가시화를 하는 것도 정확한 실험이 되는지 확인할 수 있는 방법일 것이다.
5. 결 론
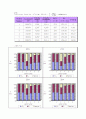
베르누이 방정식 및 이와 관련하여 유체유동 중에 일어나는 에너지 손실에 대한 개념을 이해하였고 평균유속, 동압수두(υ2/2g)를 계산하고 정압수두(p/γ)와 동압수두(υ2/2g)을 이용하여 에너지선(E.L), 수력 기울기선(H. G. L) 및 에너지 손실수두를 그래프 상에 표시하였으며 무차원수의 중요성을 이해하였다..
6. 참고 문헌
가. 유체역학 (동명사, 김영득외 3명, 2000) p75 ～ 77
나. 최신유체역학 (선학출판사, 나종문외 3명, 2001) p83 ～ 88
다. 베르누이 수에 대한 연구 : Bernoulli numbers (논문)
(엄지혜, 인하대 교육대학원, 2004)
라. 단위조작 Easy Manual 고용식저 선학출판사 p12-20(1999)
마. 단위조작 이화영외 2명 공저 McGraw-Hill Korea pp15-16, 91-120

키워드

베르누이방정식,   유체영동,   수두,   역학정에너지손실