-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
-
11
-
12
-
13
-
14
-
15
-
16
-
17
-
18
-
19
-
20
-
21
-
22
-
23
-
24
-
25
-
26
-
27
-
28
-
29
-
30
-
31
-
32
-
33
-
34
-
35
-
36
-
37
-
38
-
39


본문내용
) : y가 x의 적분값에 비례하고 것이고, 그 전달 함수는 로 되어 1형이 되므로 정상 위치 편차를 없앨 수 있다.
③ 비례 + 적분 동작(PI 동작)
인 전달 관계로 표현된다.
여기서 T1 는 I 동작의 크기 정도를 나타내는 척도이며 적분 시간 또는 reset 시간이라 하며 이 PI 동작은 지상 요소에 대응되며 정상 특성을 개선하는 데 쓰여진다.
④ 비례 + 미분 동작 (PD 동작)
로 TD를 미분시간 또는 rate 시간이라 하며, PD 동작은 진상 요소에 대응되므로 응답 속응성의 개선에 쓰여진다.
⑤ 비례 + 적분 + 미분 동작 [PID 동작]
로 이 PID 동작은 정상 특성과 응답 속응성을 동시에 개선하는 데 쓰인다.
26. 조절기의 제어 동작
27. 표준전지의 기전력
(1) 정의
F.A wolff의 식이라고도 하며 웨스톤 표준전지의 기전력을 구하는 식이다. 표준전지는 20℃ 가까운 온도에서 사용하는 것이 비람직하며 공식은 3승의 항을 생략하고 있다.
(2) 공식
28. 백분율의 오차
(1) 정의
오차의 반대를 보정이라 하고 α= T-M으로 구한다. 또(α/M)×100%를 보정오차라 한다.
(2) 공식
26. 조절기의 제어 동작
29. 분류기의 배율
(1) 정의
소형계기는 분류기를 내장하고 있으며 분류기를 2개 이상 내장하여 단자로 전환하는 multi-range의 전류계가 있다.
(2) 공식
A ra
i
I R
30. 분압기의 배율
(1) 정의
전압계의 배율기에는 보통 1V에 대하여 100Ω 정도의 망간선을 쓴다.
(2) 공식
밀리 볼트계 :
정전 전압계 :
31. 단상전력의 측정(3전압계법)
(1) 정의
부하에 직렬로 저항을 접속해서 3개의 전압계를 접속하여 각 전압계의 눈금을 측정한다. 이 때 저항 R의 전압 RI는 전류와 동상이다.
(2) 공식
32. 단상전력의 측정(3상 전류계법)
(1) 정의
3전류계법은 부하에 병렬로 저항을 접속해서 각 전류계의 값을 읽고 계산한다. 또 AB간의 전압 과 부하의 단자전압 V는 동상이다.
(2) 공식
33. 블론델의 법칙
(1) 정의
n상 교류의 전전력은 (n-1)개의 전력계의 대수합이다.
(2) 공식
n상 교류의 부하가 Y결선으로 되어 있을 때 각 상전력의 순시값의 합은 다음과 같다.
또 전류의 합은 0이므로
이것을 전력의 식에 대입해서
이 되어서 (n-1)개의 전력을 측정함으로써 전전력을 측정 할 수 있다.
34. 2상 전력계에 의한 3상전력의 측정
(1) 정의
2전력계법은 평형부하인 경우 Δ결선에서도 쓸 수 있다.
(2) 공식
[2 전력계법]
35. 휘스톤브리지의 평형조건
(1) 정의
비례변의 저항은 1, 10, 100, 1000, 10000과 같이 Ω의 값을 가졌으며, R은 1Ω 간격의 값을 갖고 있다.
(2) 공식
36. 더블 브리지의 평형 조건
(1) 정의
더블 브리지의 특징은 접촉저항의 영향이 나타나지 않는 데에 있다.
(2) 공식
37. 접지저항의 측정
(1) 정의
이 측정 해야할 접지판, 는 보조 접지판이고 는 거의 전 삼각형의 정점에 있도록 배치하여 두 개의 전극판간의 코울라브리지로 측정한다.
(2) 공식
38. 전지의 내부 저항의 측정(맨스 법)
(1) 정의
를 닫아서 전류를 조정하여 다시 를 닫아도 G의 전류가 변하지 않을 때 전지의 매부 저항을 측정할 수 있다.
(2) 공식
39. 전지의 내부 저항의 측정(전압계법)
(1) 정의
간편한 내부저항 측정법이며 내부저항이 큰 전압계를 쓴다.
(2) 공식
40. 교류 브리지의 평형 조건
(1) 정의
수화구 D의 소리가 최소일 때의 조건식에서 구하는 각 임피던스는 복소수로 계산한다.
(2) 공식
미지 임피던스 일 때
41. 고저항의 측정
(1) 정의
전압계는 가급적 저항이 큰 것을 쓴다.
(2) 공식
42. 맥스웰 브리지에 의한 L의 측정
(1) 정의
표준 자기인덕턴스와 표준저항이 있는 경우의 L의 측정법인데 측정이 간단하기 때문에 잘 쓰인다.
(2) 공식
43. 쉘링 브리지에 의한 C의 측정
(1) 정의
고압측정회로를 사용한다. 미소용량을 측정 할 수 있는데 각 변은 shield 할 필요가 있다.
(2) 공식
44. 케리포스터 브리지에 의한 M의 측정
(1) 정의
M과 L의 측정을 할 수 있다.
(2) 공식
45. 캠벨브리지에 의한 주파수의 측정
(1) 정의
상호유도인덕턴스 M을 조절해서 수화기 D의 소리가 최저 일 때에 구할 수 있는 조건식이다. 이 회로는 1kHZ 이하의 주파수 측정에 쓴다.
(2) 공식
46. 윈브리지에 의한 주파수의 측정
(1) 정의
수화구 D의 소리가 최소일 때의 식에서 구한 것이다. 가청주파까지의 광범위한 주파수의 측정을 할 수 있으나, 회로 대신에 콘덴서를 넣으면 용량의 손실각을 구할 수 있다.
(2) 공식
47. Q 미터에 의한 Q의 측정
(1) 정의
콘덴서 C를 가감해서 의 전압이 최대가 되도록 하고 이 때의 전압을 로 하면 최대에서 공진이 일어나고 있다.
(2) 공식
48. Q 미터에 의한 L의 측정
(1) 정의
콘덴서 C를 가감해서 의 지시를 보는데 지침이 최대를 가리키고 있을 때 공진이 일어난다.
(2) 공식
49. Q 미터에 의한 C의 측정
(1) 정의
보조코일 L은 일정한 것을 쓴다. 서 를 가감해서 의 지시를 보는데 지침이 최대를 가리키고 있을 때 공진이 일어난다. 피측 콘덴서 를 접속하지 않았을 때의 공진시의 의 값을 구한다.
(2) 공식
50. 각종 유량계의 측정
(1) 차압식 유량계
조리개 전후에 유량의 제곱에 비례한 압력차가 발생한다(베르누이의 정리).
(2) 면적식 유량계
통과 면적을 바꾸어 차압을 일정하게 한다 (베르누이의 정리).
(2) 면적식 유량계
통과 면적을 바꾸어 차압을 일정하게 한다 (베르누이의 정리).
(3) 용적식 유량계
계량실의 회전수를 계측한다.
(4) 임펠러(Turbine) 유량계
임펠러의 회전수를 계측한다.
(5) 전자식 유량계
페러디의 법칙을 이용한다.
(6) 초음파식 유량계
초음파의 전달속도를 계측하여 유량을 측정한다.
(7) 동압식(피토관) 유량계
동압과 정압을 이용하여 유량을 측정한다 (베르누이의 정리).
(8) 격막식 유량계
베르누이의 정리
③ 비례 + 적분 동작(PI 동작)
인 전달 관계로 표현된다.
여기서 T1 는 I 동작의 크기 정도를 나타내는 척도이며 적분 시간 또는 reset 시간이라 하며 이 PI 동작은 지상 요소에 대응되며 정상 특성을 개선하는 데 쓰여진다.
④ 비례 + 미분 동작 (PD 동작)
로 TD를 미분시간 또는 rate 시간이라 하며, PD 동작은 진상 요소에 대응되므로 응답 속응성의 개선에 쓰여진다.
⑤ 비례 + 적분 + 미분 동작 [PID 동작]
로 이 PID 동작은 정상 특성과 응답 속응성을 동시에 개선하는 데 쓰인다.
26. 조절기의 제어 동작
27. 표준전지의 기전력
(1) 정의
F.A wolff의 식이라고도 하며 웨스톤 표준전지의 기전력을 구하는 식이다. 표준전지는 20℃ 가까운 온도에서 사용하는 것이 비람직하며 공식은 3승의 항을 생략하고 있다.
(2) 공식
28. 백분율의 오차
(1) 정의
오차의 반대를 보정이라 하고 α= T-M으로 구한다. 또(α/M)×100%를 보정오차라 한다.
(2) 공식
26. 조절기의 제어 동작
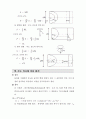
29. 분류기의 배율
(1) 정의
소형계기는 분류기를 내장하고 있으며 분류기를 2개 이상 내장하여 단자로 전환하는 multi-range의 전류계가 있다.
(2) 공식
A ra
i
I R
30. 분압기의 배율
(1) 정의
전압계의 배율기에는 보통 1V에 대하여 100Ω 정도의 망간선을 쓴다.
(2) 공식
밀리 볼트계 :
정전 전압계 :
31. 단상전력의 측정(3전압계법)
(1) 정의
부하에 직렬로 저항을 접속해서 3개의 전압계를 접속하여 각 전압계의 눈금을 측정한다. 이 때 저항 R의 전압 RI는 전류와 동상이다.
(2) 공식
32. 단상전력의 측정(3상 전류계법)
(1) 정의
3전류계법은 부하에 병렬로 저항을 접속해서 각 전류계의 값을 읽고 계산한다. 또 AB간의 전압 과 부하의 단자전압 V는 동상이다.
(2) 공식
33. 블론델의 법칙
(1) 정의
n상 교류의 전전력은 (n-1)개의 전력계의 대수합이다.
(2) 공식
n상 교류의 부하가 Y결선으로 되어 있을 때 각 상전력의 순시값의 합은 다음과 같다.
또 전류의 합은 0이므로
이것을 전력의 식에 대입해서
이 되어서 (n-1)개의 전력을 측정함으로써 전전력을 측정 할 수 있다.
34. 2상 전력계에 의한 3상전력의 측정
(1) 정의
2전력계법은 평형부하인 경우 Δ결선에서도 쓸 수 있다.
(2) 공식
[2 전력계법]
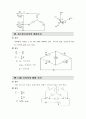
35. 휘스톤브리지의 평형조건
(1) 정의
비례변의 저항은 1, 10, 100, 1000, 10000과 같이 Ω의 값을 가졌으며, R은 1Ω 간격의 값을 갖고 있다.
(2) 공식
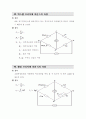
36. 더블 브리지의 평형 조건
(1) 정의
더블 브리지의 특징은 접촉저항의 영향이 나타나지 않는 데에 있다.
(2) 공식
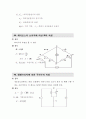
37. 접지저항의 측정
(1) 정의
이 측정 해야할 접지판, 는 보조 접지판이고 는 거의 전 삼각형의 정점에 있도록 배치하여 두 개의 전극판간의 코울라브리지로 측정한다.
(2) 공식
38. 전지의 내부 저항의 측정(맨스 법)
(1) 정의
를 닫아서 전류를 조정하여 다시 를 닫아도 G의 전류가 변하지 않을 때 전지의 매부 저항을 측정할 수 있다.
(2) 공식
39. 전지의 내부 저항의 측정(전압계법)
(1) 정의
간편한 내부저항 측정법이며 내부저항이 큰 전압계를 쓴다.
(2) 공식
40. 교류 브리지의 평형 조건
(1) 정의
수화구 D의 소리가 최소일 때의 조건식에서 구하는 각 임피던스는 복소수로 계산한다.
(2) 공식
미지 임피던스 일 때
41. 고저항의 측정
(1) 정의
전압계는 가급적 저항이 큰 것을 쓴다.
(2) 공식
42. 맥스웰 브리지에 의한 L의 측정
(1) 정의
표준 자기인덕턴스와 표준저항이 있는 경우의 L의 측정법인데 측정이 간단하기 때문에 잘 쓰인다.
(2) 공식
43. 쉘링 브리지에 의한 C의 측정
(1) 정의
고압측정회로를 사용한다. 미소용량을 측정 할 수 있는데 각 변은 shield 할 필요가 있다.
(2) 공식
44. 케리포스터 브리지에 의한 M의 측정
(1) 정의
M과 L의 측정을 할 수 있다.
(2) 공식
45. 캠벨브리지에 의한 주파수의 측정
(1) 정의
상호유도인덕턴스 M을 조절해서 수화기 D의 소리가 최저 일 때에 구할 수 있는 조건식이다. 이 회로는 1kHZ 이하의 주파수 측정에 쓴다.
(2) 공식
46. 윈브리지에 의한 주파수의 측정
(1) 정의
수화구 D의 소리가 최소일 때의 식에서 구한 것이다. 가청주파까지의 광범위한 주파수의 측정을 할 수 있으나, 회로 대신에 콘덴서를 넣으면 용량의 손실각을 구할 수 있다.
(2) 공식
47. Q 미터에 의한 Q의 측정
(1) 정의
콘덴서 C를 가감해서 의 전압이 최대가 되도록 하고 이 때의 전압을 로 하면 최대에서 공진이 일어나고 있다.
(2) 공식
48. Q 미터에 의한 L의 측정
(1) 정의
콘덴서 C를 가감해서 의 지시를 보는데 지침이 최대를 가리키고 있을 때 공진이 일어난다.
(2) 공식
49. Q 미터에 의한 C의 측정
(1) 정의
보조코일 L은 일정한 것을 쓴다. 서 를 가감해서 의 지시를 보는데 지침이 최대를 가리키고 있을 때 공진이 일어난다. 피측 콘덴서 를 접속하지 않았을 때의 공진시의 의 값을 구한다.
(2) 공식
50. 각종 유량계의 측정
(1) 차압식 유량계
조리개 전후에 유량의 제곱에 비례한 압력차가 발생한다(베르누이의 정리).
(2) 면적식 유량계
통과 면적을 바꾸어 차압을 일정하게 한다 (베르누이의 정리).
(2) 면적식 유량계
통과 면적을 바꾸어 차압을 일정하게 한다 (베르누이의 정리).
(3) 용적식 유량계
계량실의 회전수를 계측한다.
(4) 임펠러(Turbine) 유량계
임펠러의 회전수를 계측한다.
(5) 전자식 유량계
페러디의 법칙을 이용한다.
(6) 초음파식 유량계
초음파의 전달속도를 계측하여 유량을 측정한다.
(7) 동압식(피토관) 유량계
동압과 정압을 이용하여 유량을 측정한다 (베르누이의 정리).
(8) 격막식 유량계
베르누이의 정리