목차
1. 최단경로란?
2. 다익스트라(Dijkstra) 알고리즘
(1) 다익스트라 알고리즘이란?
(2) 다익스트라 알고리즘의 원리
(3) 다익스트라 알고리즘의 구체적 적용
(4) 다익스트라 알고리즘의 구현을 위한 소스코드 및 출력결과
3. 플로이드(Floyd) 알고리즘
(1) 플로이드 알고리즘이란?
(2) 플로이드 알고리즘의 원리
(3) 플로이드 알고리즘의 구체적 적용
(4) 플로이드 알고리즘의 구현을 위한 소스코드 및 출력결과
4. 다익스트라 알고리즘과 플로이드 알고리즘의 비교
2. 다익스트라(Dijkstra) 알고리즘
(1) 다익스트라 알고리즘이란?
(2) 다익스트라 알고리즘의 원리
(3) 다익스트라 알고리즘의 구체적 적용
(4) 다익스트라 알고리즘의 구현을 위한 소스코드 및 출력결과
3. 플로이드(Floyd) 알고리즘
(1) 플로이드 알고리즘이란?
(2) 플로이드 알고리즘의 원리
(3) 플로이드 알고리즘의 구체적 적용
(4) 플로이드 알고리즘의 구현을 위한 소스코드 및 출력결과
4. 다익스트라 알고리즘과 플로이드 알고리즘의 비교
본문내용
정 점
1
2
3
4
5
6
1
0
9
3
18
20
23
2
∞
0
∞
∞
∞
30
3
∞
6
0
15
21
24
4
∞
25
∞
0
6
9
5
∞
∞
∞
∞
0
3
6
∞
∞
∞
∞
∞
0
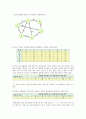
이와 같은 테이블을 활용하게 되면 각 정점 사이의 최단거리를 한꺼번에 구할 수 있게 된다.
예를 들어 1번 정점과 4번 정점의 최단거리는 18이 되는 것이다.
각 정점간의 최소이동 경로를 추적하고 싶으면, 테이블에 이전에 연결된 정점을 저장하고 기억해 두면 된다.
다음 테이블은 각 정점이 어느 정점에서부터 왔는지 기록한 테이블이다. 이 테이블을 이용하여, 각 정점의 최단거리가 어떠한 경로로 형성이 되어있는지에 대해서 추적할 수 있다.
정 점
1
2
3
4
5
6
1
0
3
1
3
1
5
2
∞
0
∞
∞
∞
2
3
∞
3
0
3
4
5
4
∞
4
∞
0
4
5
5
∞
∞
∞
∞
0
5
6
∞
∞
∞
∞
∞
0
예를 들어 1번 정점에서 4번 정점의 최단 거리는 18이 되는데, 이것이 역추적을 통해서 어떠한 경로를 가지게 되는지 알아보도록 하면 다음과 같다.
테이블(이하 t)에서 t[1, 4]를 보면 3이 나오게 되고, t[1, 3]을 찾아가면 1이 나오는 것을 볼 수 있다. 여기서 시작점이 1이므로 역추적을 통해 1을 찾아냈다면 이 과정을 완료하게 되는 것이다.
이제 나왔던 수들을 거꾸로 나열하게 되면, 1, 3, 4가 되고 이는 1 → 3 → 4의 경로를 통해 최단경로가 형성되었다는 것을 의미한다.
(4) 플로이드 알고리즘의 구현을 위한 소스코드 및 출력결과
#include
struct node_info{
double dist;
int from;
int flag;
}node_info;
double dist_table[14][14]={
{0,3.334,4.474,100,1.306,7.4,100,3,100,100,100,100,100,100},{3.334,0,1.14,100,4.32,4.14,100,2.16,100,100,100,100,100,100},{4.474,1.14,0,100,5.22,3.28,100,2.68,100,100,100,100,100,100}
,{100,100,100,0,100,3.26,3.04,100,100,100,100,100,100,100}
,{1.306,4.32,5.22,100,0,8.2,3.38,100,100,100,3.5,100,100,100}
,{7.4,4.14,3.28,3.26,8.2,0,2.16,5.04,2.36,2.44,100,100,6.36,6.28}
,{100,100,100,3.04,3.38,2.16,0,100,100,2.96,100,100,100,100}
,{3,2.16,2.68,100,100,5.04,100,0,100,100,100,100,100,100}
,{100,100,100,100,100,2.36,100,100,0,1.84,100,100,4.56,5.06}
,{100,100,100,100,100,2.44,2.96,100,1.84,0,100,100,4.08,3.9}
,{100,100,100,100,3.5,100,100,100,100,100,0,100,100,100}
,{100,100,100,100,100,100,100,100,100,100,100,0,2.24,100}
,{100,100,100,100,100,6.36,100,100,4.56,4.08,100,2.24,0,1.72}
,{100,100,100,100,100,6.28,100,100,5.06,3.9,100,100,1.72,0} };
void main()
{
int start,finish;
printf(\"출발점과 도착점을 입력 ex)1~5 : \");
scanf(\"%d~%d\",&start,&finish);
printf(\"출발점 %d이고 도착점 %d \\n\",start,finish);
start--;
finish--;
int i,k;
double min;
struct node_info city[14];
for (i=0; i<14;i++)
{
city[i].dist = dist_table[finish][i];
city[i].from = finish;
city[i].flag = 0;
}
city[finish].dist = 0;
city[finish].from = finish;
city[finish].flag = 1;
int p = finish;
for(i=0;i<12;i++)
{
min = 100;
for (k=0;k<14;k++)
{
if ((city[k].flag == 0)&&(min > city[k].dist))
{
min = city[k].dist;
p = k;
}
}
city[p].flag = 1;
for (k=0;k<14;k++)
{
if(city[k].dist > (min + dist_table[p][k]))
{
city[k].dist = min + dist_table[p][k];
city[k].from = p;
}
}
}
printf(\"출발점 %d과 도착점 %d의 최단 거리 :
%f\\n\" , start+1, finish+1, city[start].dist );
printf(\"그리고 최단경로는 : \");
p = start;
while(true)
{
printf(\"%d => \", p +1);
p = city[p].from;
if (p == finish)
{
printf(\"%d\\n\", p+1);
break;
}
}
return;
}
소스코드
출력결과
4. 다익스트라 알고리즘과 플로이드 알고리즘의 비교
다익스트라 알고리즘은 한 시작점을 잡고 그 시작점을 제외한 모든 정점의 최단경로를 구해내지만, 플로이드 알고리즘은 모든 정점간의 최단 경로를 한 번에 구해낼 수 있다. 이는 모든 구간간의 최단경로를 구하고 싶을 때 플로이드 알고리즘이 유리하다는 것이 된다.
다익스트라 알고리즘은 시간복잡도가 n²이 되지만, 플로이드 알고리즘을 사용하게 되면 n³이 된다. 이는 다익스트라 알고리즘이 최단경로를 구할 때 더 빠른 시간에 결과를 가져다 줄 수 있다는 것을 의미한다. 물론 다익스트라 알고리즘을 n번 돌리면, n³이 되면서 모든 정점간의 최단경로를 구할 수도 있다.
1
2
3
4
5
6
1
0
9
3
18
20
23
2
∞
0
∞
∞
∞
30
3
∞
6
0
15
21
24
4
∞
25
∞
0
6
9
5
∞
∞
∞
∞
0
3
6
∞
∞
∞
∞
∞
0
이와 같은 테이블을 활용하게 되면 각 정점 사이의 최단거리를 한꺼번에 구할 수 있게 된다.
예를 들어 1번 정점과 4번 정점의 최단거리는 18이 되는 것이다.
각 정점간의 최소이동 경로를 추적하고 싶으면, 테이블에 이전에 연결된 정점을 저장하고 기억해 두면 된다.
다음 테이블은 각 정점이 어느 정점에서부터 왔는지 기록한 테이블이다. 이 테이블을 이용하여, 각 정점의 최단거리가 어떠한 경로로 형성이 되어있는지에 대해서 추적할 수 있다.
정 점
1
2
3
4
5
6
1
0
3
1
3
1
5
2
∞
0
∞
∞
∞
2
3
∞
3
0
3
4
5
4
∞
4
∞
0
4
5
5
∞
∞
∞
∞
0
5
6
∞
∞
∞
∞
∞
0
예를 들어 1번 정점에서 4번 정점의 최단 거리는 18이 되는데, 이것이 역추적을 통해서 어떠한 경로를 가지게 되는지 알아보도록 하면 다음과 같다.
테이블(이하 t)에서 t[1, 4]를 보면 3이 나오게 되고, t[1, 3]을 찾아가면 1이 나오는 것을 볼 수 있다. 여기서 시작점이 1이므로 역추적을 통해 1을 찾아냈다면 이 과정을 완료하게 되는 것이다.
이제 나왔던 수들을 거꾸로 나열하게 되면, 1, 3, 4가 되고 이는 1 → 3 → 4의 경로를 통해 최단경로가 형성되었다는 것을 의미한다.
(4) 플로이드 알고리즘의 구현을 위한 소스코드 및 출력결과
#include
struct node_info{
double dist;
int from;
int flag;
}node_info;
double dist_table[14][14]={
{0,3.334,4.474,100,1.306,7.4,100,3,100,100,100,100,100,100},{3.334,0,1.14,100,4.32,4.14,100,2.16,100,100,100,100,100,100},{4.474,1.14,0,100,5.22,3.28,100,2.68,100,100,100,100,100,100}
,{100,100,100,0,100,3.26,3.04,100,100,100,100,100,100,100}
,{1.306,4.32,5.22,100,0,8.2,3.38,100,100,100,3.5,100,100,100}
,{7.4,4.14,3.28,3.26,8.2,0,2.16,5.04,2.36,2.44,100,100,6.36,6.28}
,{100,100,100,3.04,3.38,2.16,0,100,100,2.96,100,100,100,100}
,{3,2.16,2.68,100,100,5.04,100,0,100,100,100,100,100,100}
,{100,100,100,100,100,2.36,100,100,0,1.84,100,100,4.56,5.06}
,{100,100,100,100,100,2.44,2.96,100,1.84,0,100,100,4.08,3.9}
,{100,100,100,100,3.5,100,100,100,100,100,0,100,100,100}
,{100,100,100,100,100,100,100,100,100,100,100,0,2.24,100}
,{100,100,100,100,100,6.36,100,100,4.56,4.08,100,2.24,0,1.72}
,{100,100,100,100,100,6.28,100,100,5.06,3.9,100,100,1.72,0} };
void main()
{
int start,finish;
printf(\"출발점과 도착점을 입력 ex)1~5 : \");
scanf(\"%d~%d\",&start,&finish);
printf(\"출발점 %d이고 도착점 %d \\n\",start,finish);
start--;
finish--;
int i,k;
double min;
struct node_info city[14];
for (i=0; i<14;i++)
{
city[i].dist = dist_table[finish][i];
city[i].from = finish;
city[i].flag = 0;
}
city[finish].dist = 0;
city[finish].from = finish;
city[finish].flag = 1;
int p = finish;
for(i=0;i<12;i++)
{
min = 100;
for (k=0;k<14;k++)
{
if ((city[k].flag == 0)&&(min > city[k].dist))
{
min = city[k].dist;
p = k;
}
}
city[p].flag = 1;
for (k=0;k<14;k++)
{
if(city[k].dist > (min + dist_table[p][k]))
{
city[k].dist = min + dist_table[p][k];
city[k].from = p;
}
}
}
printf(\"출발점 %d과 도착점 %d의 최단 거리 :
%f\\n\" , start+1, finish+1, city[start].dist );
printf(\"그리고 최단경로는 : \");
p = start;
while(true)
{
printf(\"%d => \", p +1);
p = city[p].from;
if (p == finish)
{
printf(\"%d\\n\", p+1);
break;
}
}
return;
}
소스코드
출력결과
4. 다익스트라 알고리즘과 플로이드 알고리즘의 비교
다익스트라 알고리즘은 한 시작점을 잡고 그 시작점을 제외한 모든 정점의 최단경로를 구해내지만, 플로이드 알고리즘은 모든 정점간의 최단 경로를 한 번에 구해낼 수 있다. 이는 모든 구간간의 최단경로를 구하고 싶을 때 플로이드 알고리즘이 유리하다는 것이 된다.
다익스트라 알고리즘은 시간복잡도가 n²이 되지만, 플로이드 알고리즘을 사용하게 되면 n³이 된다. 이는 다익스트라 알고리즘이 최단경로를 구할 때 더 빠른 시간에 결과를 가져다 줄 수 있다는 것을 의미한다. 물론 다익스트라 알고리즘을 n번 돌리면, n³이 되면서 모든 정점간의 최단경로를 구할 수도 있다.
































소개글