공학통계

본문내용

제7장 확률변수의 함수의 분포
1. 확률변수의 함수
1) 정의
확률변수 의 함수를 라 하면, 는 새로운 확률변수가 되며, 확률변수 의 확률분포는 확률변수 의 분포에 의하여 결정됨.
2) 용도
① 확률변수 자체로서 유용
② 통계적 분석시 유용
2. 이산형 확률변수의 함수
1) 하나의 변수의 함수
《정리》는 확률분포가 인 이산형 확률변수이고, 와 사이에는 라는 1 대 1 대응관계가 성립하며, 를 에 대하여 풀면 유일하게 로 될 때 의 확률분포 는 다음과 같음.
예) 확률변수 의 분포함수가 다음과 같은 기하분포를 따를 때 의 확률분포를 구하라.
풀이)
2) 두 개의 변수의 함수
《정리》과 는 결합확률분포가 인 이산형 확률변수이고, 와 는 서로 1 대 1로 대응하여 식 과 를 과 에 대하여 풀면 유일하게 , 로 될 때, 과 로 정의되는 새로운 확률변수 과 의 결합확률분포 는 다음과 같음.
또한 의 확률분포를 이라 하면,
예) 확률변수 과 가 각각 모수가 인 포아송 분포를 따르고 서로 독립이라고 할 때 ,의 확률분포를 구하라.
풀이)
단 ,
ㆍ과 를 역변환시키면 , 이 되므로 앞의 정리를 이용하여 과 의 결합확률분포 를 구하면 다음과 같음.
( 이므로 로부터 는 보다 작거나 같아야 됨)
ㆍ에 대한 주변확률분포 를 구하면 다음과 같게 됨.
모수가 과 인 포아송 분포를 따르는 서로 독립인 두 확률변수의 합은 모수가 인 포아송 분포를 따르게 됨.
3. 연속형 확률변수의 함수
1) 하나의 변수의 함수
《정리》는 확률밀도함수가 인 연속형 확률변수이고 와 사이에는 라는 1 대 1 대응관계가 성립하여, 관계식 를 에 대하여 풀면 유일하게 로 될 때 의 확률밀도함수 는 다음과 같음.
증명)
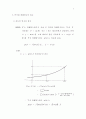
ⅰ) 가 증가함수인 경우
의 확률밀도함수 는
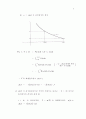
ⅱ) 가 감소함수인 경우
의 확률밀도함수 는
※ 가 감소함수이므로 곡선의 기울기는 음이고 이므로 증가함수의 경우와 같게 됨.
ⅰ), ⅱ) 의 결과로부터, 의 확률밀도함수 는
예) 가 연속형 확률변수이고 가 다음과 같을 때 의 확률밀도함수를 구하라.
풀이) 으로부터가 되고,
2) 두 개의 변수의 함수
《정리》과 는 결합확률밀도함수가 인 연속형 확률변수이고, 와 는 서로 1 대 1로 대응하여 식 과 를 과 에 대하여 풀면 유일하게 과 로 될 때, 과 의 결합밀도함수 는 다음과 같음.
예) 과 의 결합확률 밀도함수가 다음과 같을 때 과 의 결합밀도함수를 구하라.
풀이)과 를 각각 에 대해 풀면,
평면에서 정의된 점의 집합 A와 대응된 평면에서 정의된 점의 집합 B를 구하기 위하여 그리고 로 놓으면, 집합 A의 경계선은 이 됨.
집합 A와 B는 다음과 같고 서로 1 대 1로 대응하게 됨.
구하고자 하는 과 의 결합확률밀도함수 는

키워드

통계,   공학통계,   확률