-
 1
1
-
 2
2
-
 3
3
-
 4
4
-
 5
5
-
 6
6
-
 7
7
-
 8
8
-
 9
9
-
 10
10
-
 11
11
-
 12
12
-
 13
13
-
 14
14
-
 15
15
-
 16
16
-
 17
17
-
 18
18
-
 19
19
-
 20
20
-
 21
21
-
 22
22
-
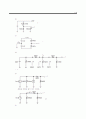 23
23
-
 24
24
-
 25
25
-
 26
26
-
 27
27
-
 28
28
-
 29
29
-
 30
30
-
 31
31
-
 32
32
-
 33
33
-
 34
34
-
 35
35
-
 36
36
-
 37
37
-
 38
38
-
 39
39
-
 40
40
-
 41
41
-
 42
42
-
 43
43
-
 44
44
-
 45
45
-
 46
46
-
 47
47
-
 48
48
-
 49
49
-
 50
50
-
 51
51
-
 52
52
-
 53
53
-
 54
54
-
 55
55
-
 56
56
-
 57
57
-
 58
58
-
 59
59
-
 60
60
-
 61
61
-
 62
62
-
 63
63
-
 64
64
-
 65
65
-
 66
66
-
 67
67
-
 68
68
-
 69
69
-
 70
70
-
 71
71
-
 72
72
-
 73
73
-
 74
74
-
 75
75
-
 76
76
-
 77
77
-
 78
78
-
 79
79
-
 80
80
-
 81
81
-
 82
82
-
 83
83
-
 84
84
-
 85
85
-
 86
86
-
 87
87
-
 88
88
-
 89
89
-
 90
90
-
 91
91
-
 92
92
-
 93
93
-
 94
94
-
 95
95
-
 96
96
-
 97
97
-
 98
98
-
 99
99
-
 100
100
-
 101
101
-
 102
102
-
 103
103
-
 104
104
-
 105
105
-
 106
106
-
 107
107
-
 108
108
-
 109
109
-
 110
110
-
 111
111
-
 112
112
-
 113
113
-
 114
114
-
 115
115
-
 116
116
-
 117
117
-
 118
118
-
 119
119
-
 120
120
-
 121
121
-
 122
122
-
 123
123
-
 124
124
-
 125
125
-
 126
126
-
 127
127
-
 128
128
-
 129
129
-
 130
130
-
 131
131
-
 132
132
-
 133
133
-
 134
134
-
 135
135
-
 136
136
-
 137
137
-
 138
138
-
 139
139
-
 140
140
-
 141
141
-
 142
142
-
 143
143
-
 144
144
-
 145
145
-
 146
146
-
 147
147
-
 148
148
-
 149
149
-
 150
150
-
 151
151
-
 152
152
-
 153
153
-
 154
154
-
 155
155
-
 156
156
-
 157
157
-
 158
158
-
 159
159
-
 160
160
-
 161
161
-
 162
162
-
 163
163
-
 164
164
-
 165
165
-
 166
166
-
 167
167
-
 168
168
-
 169
169
-
 170
170
-
 171
171
-
 172
172
-
 173
173
-
 174
174
-
 175
175
-
 176
176
-
 177
177
-
 178
178
-
 179
179
-
 180
180
-
 181
181
-
 182
182
-
 183
183
-
 184
184
-
 185
185
-
 186
186
-
 187
187
-
 188
188
-
 189
189
-
 190
190
-
 191
191
-
 192
192
-
 193
193
-
 194
194
-
 195
195
-
 196
196
-
 197
197
-
 198
198
-
 199
199
-
 200
200
-
 201
201
-
 202
202
-
 203
203
-
 204
204
-
 205
205
-
 206
206
-
 207
207
-
 208
208
-
 209
209
-
 210
210
-
 211
211
-
 212
212
-
 213
213
-
 214
214
-
 215
215
-
 216
216
-
 217
217
-
 218
218
-
 219
219
-
 220
220
-
 221
221
-
 222
222
-
 223
223
-
 224
224
-
 225
225
-
 226
226
-
 227
227
-
 228
228
-
 229
229
-
 230
230
-
 231
231
-
 232
232
-
 233
233
-
 234
234
-
 235
235
-
 236
236
-
 237
237
-
 238
238
-
 239
239
-
 240
240
-
 241
241
-
 242
242
-
 243
243
-
 244
244
-
 245
245
본 자료는 10페이지 의 미리보기를 제공합니다. 이미지를 클릭하여 주세요.

-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
-
11
-
12
-
13
-
14
-
15
-
16
-
17
-
18
-
19
-
20
-
21
-
22
-
23
-
24
-
25
-
26
-
27
-
28
-
29
-
30
-
31
-
32
-
33
-
34
-
35
-
36
-
37
-
38
-
39
-
40
-
41
-
42
-
43
-
44
-
45
-
46
-
47
-
48
-
49
-
50
-
51
-
52
-
53
-
54
-
55
-
56
-
57
-
58
-
59
-
60
-
61
-
62
-
63
-
64
-
65
-
66
-
67
-
68
-
69
-
70
-
71
-
72
-
73
-
74
-
75
-
76
-
77
-
78
-
79
-
80
-
81
-
82
-
83
-
84
-
85
-
86
-
87
-
88
-
89
-
90
-
91
-
92
-
93
-
94
-
95
-
96
-
97
-
98
-
99
-
100
-
101
-
102
-
103
-
104
-
105
-
106
-
107
-
108
-
109
-
110
-
111
-
112
-
113
-
114
-
115
-
116
-
117
-
118
-
119
-
120
-
121
-
122
-
123
-
124
-
125
-
126
-
127
-
128
-
129
-
130
-
131
-
132
-
133
-
134
-
135
-
136
-
137
-
138
-
139
-
140
-
141
-
142
-
143
-
144
-
145
-
146
-
147
-
148
-
149
-
150
-
151
-
152
-
153
-
154
-
155
-
156
-
157
-
158
-
159
-
160
-
161
-
162
-
163
-
164
-
165
-
166
-
167
-
168
-
169
-
170
-
171
-
172
-
173
-
174
-
175
-
176
-
177
-
178
-
179
-
180
-
181
-
182
-
183
-
184
-
185
-
186
-
187
-
188
-
189
-
190
-
191
-
192
-
193
-
194
-
195
-
196
-
197
-
198
-
199
-
200
-
201
-
202
-
203
-
204
-
205
-
206
-
207
-
208
-
209
-
210
-
211
-
212
-
213
-
214
-
215
-
216
-
217
-
218
-
219
-
220
-
221
-
222
-
223
-
224
-
225
-
226
-
227
-
228
-
229
-
230
-
231
-
232
-
233
-
234
-
235
-
236
-
237
-
238
-
239
-
240
-
241
-
242
-
243
-
244
-
245


본문내용
수이다.
(c)
13.6 에 대해, 이다. 주기는 초이다.
(a) 그리고 의 파형을 그려라.
(b) 의 푸리에 급수 전개식을 구하고, 그 결과를 논하라.
와 가 구간 내에서와 끝점, 에서 연속이므로, 고조파 진폭이 로 감소할 것으로 예상된다. 함수는 인 기함수이다. 그러므로
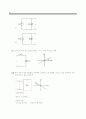
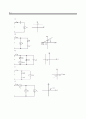
13.7 (a) 그림 P13.7에 보인 두 파형에 대한 푸리에 급수를 구하라.
이는 가 기함수이기 때문이라고 예상된다.
는 기함수이다. 그러므로 이다.
(b) 그림 P13.7(a)에 보인 파형의 푸리에 급수로부터 그림 P13.7(b)에 보인 파형의 푸리에 급수를 직접 구하는 방법을 보여라.
13.8 임의의 주기 함수 는 그것의 우함수 부분과 기함수 부분의 합으로 분해될 수 있다. 즉,
(a) 와 를 와 의 적절한 결합으로 얻을 수 있다는 것을 보여라.
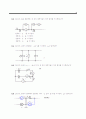
(b) (a)의 결과를 이하여, 그림 P13.8에 보인 함수의 우수 부분과 기수 부분의 파형을 구하라.
(c) 의 삼각 형식 푸리에 급수를 구하라.
이라 놓고, 는 다음과 같이 나타낼 수 있을 것이다.
또한
는 식 (13.31)로부터 구할 수 있다.
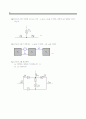
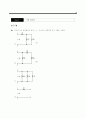
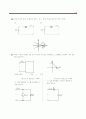
13.9 어떤 소자의 전달 특성을 그림 P13.9에 나타냈다.
(a) 입력 가 일 때, 출력이 입력에 선형적으로 관계하기 위한 조건은 무엇인가?
(b) 라고 가정하면, 출력에 어떤 고조파들이 나타나겠는가?
만약 라면 출력 파형은
그림과 같이 보일 것이다. → 이 파형은 반파 대칭성을 갖는다. 따라서 홀수 고조파들만 존재한다.
(c) 삼각 형식의 푸리에 급수 계수들을 구하기 위한 방정식을 세워라.
일때 클리핑이 발생한다. 이는 일 때 발생한다.
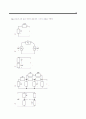
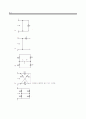
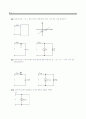
13.10 어떤 소자의 전달 특성을 그림 P13.10에 나타냈다. 라고 가정하라.
(a) 일 때, 출력 파형을 도시하고, 그것의 삼각 형식 푸리에 급수를 구하라.
는 우함수이므로 이다.
이므로 다음과 같다.
이고, 이므로, 는 또한 다음과 같이 표현될 수 있다.
(b) 일 때, 출력 파형을 도시하고, 그것의 삼각 형식 푸리에 급수를 구하라.
는 우함수이므로 이다.
(c) 를 이용하여, (a)의 해답으로부터 (b)의 해답을 구할 수 있다는 것을 보여라.
(d) 만약 가 과 약간 다르다면, (b)에서 구한 결과가 어떻게 달라지겠는가?
이면, 두 개의 높이가 다를 것이다. 결과적으로 스펙트럼에서 홀수 고조파들이 돋보일 것이다.
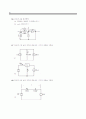
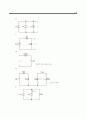
13.11 그림 P13.11에 보인 파형의 기본파 성분과 평균값 사이에는 어떤 관계가 있는가? 단, 이 펄스의 폭은 주기에 비해 좁다.
함수를 고려해 보자. →
펄스가 좁으므로
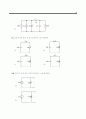
13.12 그림 P13.12에서 의 값은 고정되어 있다. 저역-통과 여파기는 무시할 수 있을 정도 의 작은 리플을 갖는 직류 출력을 만들어내기 위해 사용되었다. 리플의 기본파 성분이 직류 출력 전압의 보다 작아야 한다면, 의 크기는 얼마이어야 하는가? 입력 전압 는 동안 사인파이다.
입력의 dc 성분
입력의 기본파 성분
전달 함수는 이다.
출력의 dc 성분
출력의 기본파 성분
13.13 그림 P13.13에서 회로는 제3 고조파에 동조되어 있다. 이 회로의 대역폭이 중심 주파수의 일 때,
(a) 출력 전압의 기본파, 제3 고조파, 그리고 제5 고조파 성분을 구하라.
여파기는 제3 고조파, 에 동조되어 있고, 대역폭이 중심 주파수, 의 이므로, 따라서
(b) 제3 고조파 출력의 진폭을 기본파 및 제5 고조파 출력의 진폭과 비교하라. 단, 비교할 때, 제3 고조파의 진폭을 로 하라. 비교한 결과를 논하라.
회로는 제3 고조파의 주파수에서 거의 사인파인 출력을 나타낼 만큼 충분히 선택적이다.
13.14 그림 P13.14의 대역-저지 회로는 입력의 기본 주파수, 즉 에 동조되어 있다. 이 회로의 주파수 제거 대역폭이 좁다고 가정하고,
(a) 출력 전압을 구하라.
(b) 를 그래프로 그리고, 값들을 표시하라.
입력 파형의 기본파 성분, 는 여파기에 의해 완전히 제거된다. 대역폭 가 매우 좁으므로, 남은 고조파들은 [이고, 인 상태로] 완전히 통과된다. 이러한 결과는 아래에 나타낸 와 대 의 곡선으로부터 명확히 볼 수 있다.
따라서 출력 파형은 입력 파형으로부터 기본파 성분을 제거하여 얻을 수 있다.
“입력에서 기본파 제거”, “출력 파형”
13.15 그림 P13.15에 보인 파형에 대한 지수 형식 푸리에 급수를 구하라.
13.16 (a) 그림 P13.16에 보인 두 파형의 지수 형식 푸리에 급수를 구하라.
(b) (a)에서 구한 두 급수를 더했을 때, 그 결과의 급수는 어떤 파형을 나타내겠는가?
두 파형의 합은 다음과 같다. →
구형파에 대한 계수는 다음과 같이 주어진다.
(a)에서 구한 두 급수의 합은
이는 위의 결과와 일치한다.
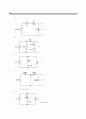
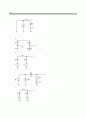
13.17 그림 P13.17에 대해,
(a) 전압 전원에 의해 전달되는 평균 전력을 파형으로부터 직접 구하라.
(b) 입력 전류의 지수 형식 푸리에 급수를 구하라.
일 때 은 다음과 같이 주어진다.
이므로 은 다음과 같이 쓸 수 있다.
이고, 이므로 다음과 같이 쓸 수 있다.
(c) 입력 전류와 입력 전압의 지수 형식 푸리에 급수를 이용하여, 전압 전원에 의해 전달되는 평균 전력을 구하라. 이 결과가 (a)의 결과와 일치하는가?
(d) 입력 전압의 지수 형식 푸리에 급수를 이용하여, 저항기에 전달된 평균 전력을 구하라. 이 결과가 (a)의 결과와 일치하는가?
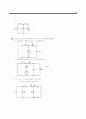
13.18 그림 P13.18에서 에 대해 이고, 에 대해 이다. 라고 가정한다.
(a) 지수 형식 푸리에 급수의 계수들을 구하라.
(b) 이라고 하라. 이 때 그 결과의 함수가 구형파의 푸리에 급수를 나타낸다는 것을 증명하라.
(a)
일 때 이다. 따라서 은 다음과 같이 근사화될 수 있다.
(b) 이 됨에 따라 파형은 구형파에 근접한다. 그러면 (a)에서 구한 계수는 다음과 같이 된다.
이 계수는 피크 대 피크 진폭이 이고, 평균값이 0인 구형파에 대한 문제 13.16(b)에서 구한 결과와 일치한다.
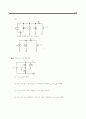
13.19 (a) 그림 P13.19에 보인 반복되는 단일-사이클 사인파의 푸리에 급수를 구하라. 단, 라고 가 정하라.
(b) 일 때, (a)에서 구한 식을 간단히 하라.
(c)
13.6 에 대해, 이다. 주기는 초이다.
(a) 그리고 의 파형을 그려라.
(b) 의 푸리에 급수 전개식을 구하고, 그 결과를 논하라.
와 가 구간 내에서와 끝점, 에서 연속이므로, 고조파 진폭이 로 감소할 것으로 예상된다. 함수는 인 기함수이다. 그러므로
13.7 (a) 그림 P13.7에 보인 두 파형에 대한 푸리에 급수를 구하라.
이는 가 기함수이기 때문이라고 예상된다.
는 기함수이다. 그러므로 이다.
(b) 그림 P13.7(a)에 보인 파형의 푸리에 급수로부터 그림 P13.7(b)에 보인 파형의 푸리에 급수를 직접 구하는 방법을 보여라.
13.8 임의의 주기 함수 는 그것의 우함수 부분과 기함수 부분의 합으로 분해될 수 있다. 즉,
(a) 와 를 와 의 적절한 결합으로 얻을 수 있다는 것을 보여라.
(b) (a)의 결과를 이하여, 그림 P13.8에 보인 함수의 우수 부분과 기수 부분의 파형을 구하라.
(c) 의 삼각 형식 푸리에 급수를 구하라.
이라 놓고, 는 다음과 같이 나타낼 수 있을 것이다.
또한
는 식 (13.31)로부터 구할 수 있다.
13.9 어떤 소자의 전달 특성을 그림 P13.9에 나타냈다.
(a) 입력 가 일 때, 출력이 입력에 선형적으로 관계하기 위한 조건은 무엇인가?
(b) 라고 가정하면, 출력에 어떤 고조파들이 나타나겠는가?
만약 라면 출력 파형은
그림과 같이 보일 것이다. → 이 파형은 반파 대칭성을 갖는다. 따라서 홀수 고조파들만 존재한다.
(c) 삼각 형식의 푸리에 급수 계수들을 구하기 위한 방정식을 세워라.
일때 클리핑이 발생한다. 이는 일 때 발생한다.
13.10 어떤 소자의 전달 특성을 그림 P13.10에 나타냈다. 라고 가정하라.
(a) 일 때, 출력 파형을 도시하고, 그것의 삼각 형식 푸리에 급수를 구하라.
는 우함수이므로 이다.
이므로 다음과 같다.
이고, 이므로, 는 또한 다음과 같이 표현될 수 있다.
(b) 일 때, 출력 파형을 도시하고, 그것의 삼각 형식 푸리에 급수를 구하라.
는 우함수이므로 이다.
(c) 를 이용하여, (a)의 해답으로부터 (b)의 해답을 구할 수 있다는 것을 보여라.
(d) 만약 가 과 약간 다르다면, (b)에서 구한 결과가 어떻게 달라지겠는가?
이면, 두 개의 높이가 다를 것이다. 결과적으로 스펙트럼에서 홀수 고조파들이 돋보일 것이다.
13.11 그림 P13.11에 보인 파형의 기본파 성분과 평균값 사이에는 어떤 관계가 있는가? 단, 이 펄스의 폭은 주기에 비해 좁다.
함수를 고려해 보자. →
펄스가 좁으므로
13.12 그림 P13.12에서 의 값은 고정되어 있다. 저역-통과 여파기는 무시할 수 있을 정도 의 작은 리플을 갖는 직류 출력을 만들어내기 위해 사용되었다. 리플의 기본파 성분이 직류 출력 전압의 보다 작아야 한다면, 의 크기는 얼마이어야 하는가? 입력 전압 는 동안 사인파이다.
입력의 dc 성분
입력의 기본파 성분
전달 함수는 이다.
출력의 dc 성분
출력의 기본파 성분
13.13 그림 P13.13에서 회로는 제3 고조파에 동조되어 있다. 이 회로의 대역폭이 중심 주파수의 일 때,
(a) 출력 전압의 기본파, 제3 고조파, 그리고 제5 고조파 성분을 구하라.
여파기는 제3 고조파, 에 동조되어 있고, 대역폭이 중심 주파수, 의 이므로, 따라서
(b) 제3 고조파 출력의 진폭을 기본파 및 제5 고조파 출력의 진폭과 비교하라. 단, 비교할 때, 제3 고조파의 진폭을 로 하라. 비교한 결과를 논하라.
회로는 제3 고조파의 주파수에서 거의 사인파인 출력을 나타낼 만큼 충분히 선택적이다.
13.14 그림 P13.14의 대역-저지 회로는 입력의 기본 주파수, 즉 에 동조되어 있다. 이 회로의 주파수 제거 대역폭이 좁다고 가정하고,
(a) 출력 전압을 구하라.
(b) 를 그래프로 그리고, 값들을 표시하라.
입력 파형의 기본파 성분, 는 여파기에 의해 완전히 제거된다. 대역폭 가 매우 좁으므로, 남은 고조파들은 [이고, 인 상태로] 완전히 통과된다. 이러한 결과는 아래에 나타낸 와 대 의 곡선으로부터 명확히 볼 수 있다.
따라서 출력 파형은 입력 파형으로부터 기본파 성분을 제거하여 얻을 수 있다.
“입력에서 기본파 제거”, “출력 파형”
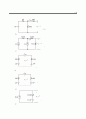
13.15 그림 P13.15에 보인 파형에 대한 지수 형식 푸리에 급수를 구하라.
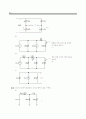
13.16 (a) 그림 P13.16에 보인 두 파형의 지수 형식 푸리에 급수를 구하라.
(b) (a)에서 구한 두 급수를 더했을 때, 그 결과의 급수는 어떤 파형을 나타내겠는가?
두 파형의 합은 다음과 같다. →
구형파에 대한 계수는 다음과 같이 주어진다.
(a)에서 구한 두 급수의 합은
이는 위의 결과와 일치한다.
13.17 그림 P13.17에 대해,
(a) 전압 전원에 의해 전달되는 평균 전력을 파형으로부터 직접 구하라.
(b) 입력 전류의 지수 형식 푸리에 급수를 구하라.
일 때 은 다음과 같이 주어진다.
이므로 은 다음과 같이 쓸 수 있다.
이고, 이므로 다음과 같이 쓸 수 있다.
(c) 입력 전류와 입력 전압의 지수 형식 푸리에 급수를 이용하여, 전압 전원에 의해 전달되는 평균 전력을 구하라. 이 결과가 (a)의 결과와 일치하는가?
(d) 입력 전압의 지수 형식 푸리에 급수를 이용하여, 저항기에 전달된 평균 전력을 구하라. 이 결과가 (a)의 결과와 일치하는가?
13.18 그림 P13.18에서 에 대해 이고, 에 대해 이다. 라고 가정한다.
(a) 지수 형식 푸리에 급수의 계수들을 구하라.
(b) 이라고 하라. 이 때 그 결과의 함수가 구형파의 푸리에 급수를 나타낸다는 것을 증명하라.
(a)
일 때 이다. 따라서 은 다음과 같이 근사화될 수 있다.
(b) 이 됨에 따라 파형은 구형파에 근접한다. 그러면 (a)에서 구한 계수는 다음과 같이 된다.
이 계수는 피크 대 피크 진폭이 이고, 평균값이 0인 구형파에 대한 문제 13.16(b)에서 구한 결과와 일치한다.
13.19 (a) 그림 P13.19에 보인 반복되는 단일-사이클 사인파의 푸리에 급수를 구하라. 단, 라고 가 정하라.
(b) 일 때, (a)에서 구한 식을 간단히 하라.


















소개글