목차
1. Changing freq.
2. Addition of Sinusoids
3. Different expression of Sinusoids sum
4. C-1.3 Lab
2. Addition of Sinusoids
3. Different expression of Sinusoids sum
4. C-1.3 Lab
본문내용
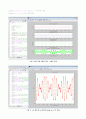
하는 곱해진 두 함수들의 진동수를 보면 200과 20으로 x1함수와 x2 함수의 차이의 반의 절반 값과 평균값과 대응됨을 확인 할 수 있다. 그리고 x3함수와 x4함수를 hold on으로 한 창에 동시에 그래프를 출력하여 비교해보니 완전히 일치한다는 결과를 얻을 수 있었다. 진폭은 x1, x2함수에 비해 합해진 결과 거의 2배로 됨을 볼 수있다. 주기의 경우 x1과 x2는 각각 1/180과 1/220 초인 반면, 그래프 상으로 관찰해보면 x3, x4함수는 주기가 0.05초임을 볼 수 있고 진동수는 20Hz로 추측해볼 수 있다.
4. C-1.3 Lab
clear all
clc
A1=20; % 나이 ; 변수들 설정
A2=1.2*A1;
M=11; % 태어난 일
D=30; % 태어난 달
T=1/4000; % 주기
tm1=(37.2/M)*T;
tm2=((-41.3)/D)*T;
t=-T:0.000001:T; % 타임 도메인 설정
x1=A1*cos(2*pi*4000*(t-tm1)); %함수들 설정
x2=A2*cos(2*pi*4000*(t-tm2));
x3=x1+x2;
subplot(3,1,1)
plot(t,x1,\'r\'); % 타임 도메인 상에서 x1함수를 continous한 빨간색 그래프로 나타냄
axis([-T T -40 40]); % 잘보이게 축 설정
title(\'x1 fucntion : A1*cos(2*pi*4000*(t-tm1)) \'); % 그래프 제목 설정
xlabel(\'Time(t): -T~T\'); %x축 이름 설정
ylabel(\'x1\'); %y축 이름 설정
hold on
subplot(3,1,2)
plot(t,x2, \'b\'); % 타임 도메인 상에서 x2함수를 continous한 초록색 그래프로 나타냄
axis([-T T -40 40]); % 잘보이게 축 설정
title(\'x2 function : A2*cos(2*pi*4000*(t-tm2))\'); % 그래프 제목 설정
xlabel(\'Time(t): -T~T\'); %x축 이름 설정
ylabel(\'x2\'); %y축 이름 설정
hold on
subplot(3,1,3)
plot(t,x3, \'g--\'); % 타임 도메인 상에서 x3함수를 쇄선 모양의 초록색 그래프로 나타냄
axis([-T T -40 40]); % 잘보이게 축 설정
title(\'x3 function : x1+x2 \'); % 그래프 제목 설정
xlabel(\'Time(t): -T~T\'); %x축 이름 설정
ylabel(\'x3=x1+x2\'); %y축 이름 설정
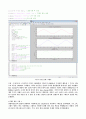
고찰 : 우선적으로 이 함수의 주기를 구해야한다. 진동수가 4000Hz로 주어졌기 때문에 그 주기는 진동수의 역수인 1/4000로 구하였다. 나머지 변수들은 본인의 나이와 생년월일에 맞게 변수 값을 지정했다. time domain의 샘플의 경우 25개 이상이 되게 충분히 많은 샘플들을 주었다. 위상은 8000pi*tm1 과 8000pi* tm2정도 코사인 함수와 차이가 났다. time domain자체를 -T부터 T까지 잡았으므로 당연히 2개의 주기가 나왔고 x1과 x2는 원점을 기준으로 대칭이다. 진폭은 x1은 A1이고 x2는 A2이다. x3는 A1+A2보다 약간 작음을 볼 수 있다. 본 문제는 간단히 x1함수와 x2함수의 합을 그래프로 표현을 하는 문제였다.
* HW2 최종 고찰 *
정현파신호들의 합성과 관련하여 다양하게 plot subplot등을 이용하여 그래프를 출력하였다. x축, y축, 그래프 제목도 따로 지정하였고 그래프를 구별하기 위해 선의 모양, 색들을 변형해보기도 하였다. 정현파 신호의 기본구성요소인 진동수, 주기, 진폭, 위상 관점에서 문제의 의미를 분석해보았다.
4. C-1.3 Lab
clear all
clc
A1=20; % 나이 ; 변수들 설정
A2=1.2*A1;
M=11; % 태어난 일
D=30; % 태어난 달
T=1/4000; % 주기
tm1=(37.2/M)*T;
tm2=((-41.3)/D)*T;
t=-T:0.000001:T; % 타임 도메인 설정
x1=A1*cos(2*pi*4000*(t-tm1)); %함수들 설정
x2=A2*cos(2*pi*4000*(t-tm2));
x3=x1+x2;
subplot(3,1,1)
plot(t,x1,\'r\'); % 타임 도메인 상에서 x1함수를 continous한 빨간색 그래프로 나타냄
axis([-T T -40 40]); % 잘보이게 축 설정
title(\'x1 fucntion : A1*cos(2*pi*4000*(t-tm1)) \'); % 그래프 제목 설정
xlabel(\'Time(t): -T~T\'); %x축 이름 설정
ylabel(\'x1\'); %y축 이름 설정
hold on
subplot(3,1,2)
plot(t,x2, \'b\'); % 타임 도메인 상에서 x2함수를 continous한 초록색 그래프로 나타냄
axis([-T T -40 40]); % 잘보이게 축 설정
title(\'x2 function : A2*cos(2*pi*4000*(t-tm2))\'); % 그래프 제목 설정
xlabel(\'Time(t): -T~T\'); %x축 이름 설정
ylabel(\'x2\'); %y축 이름 설정
hold on
subplot(3,1,3)
plot(t,x3, \'g--\'); % 타임 도메인 상에서 x3함수를 쇄선 모양의 초록색 그래프로 나타냄
axis([-T T -40 40]); % 잘보이게 축 설정
title(\'x3 function : x1+x2 \'); % 그래프 제목 설정
xlabel(\'Time(t): -T~T\'); %x축 이름 설정
ylabel(\'x3=x1+x2\'); %y축 이름 설정
고찰 : 우선적으로 이 함수의 주기를 구해야한다. 진동수가 4000Hz로 주어졌기 때문에 그 주기는 진동수의 역수인 1/4000로 구하였다. 나머지 변수들은 본인의 나이와 생년월일에 맞게 변수 값을 지정했다. time domain의 샘플의 경우 25개 이상이 되게 충분히 많은 샘플들을 주었다. 위상은 8000pi*tm1 과 8000pi* tm2정도 코사인 함수와 차이가 났다. time domain자체를 -T부터 T까지 잡았으므로 당연히 2개의 주기가 나왔고 x1과 x2는 원점을 기준으로 대칭이다. 진폭은 x1은 A1이고 x2는 A2이다. x3는 A1+A2보다 약간 작음을 볼 수 있다. 본 문제는 간단히 x1함수와 x2함수의 합을 그래프로 표현을 하는 문제였다.
* HW2 최종 고찰 *
정현파신호들의 합성과 관련하여 다양하게 plot subplot등을 이용하여 그래프를 출력하였다. x축, y축, 그래프 제목도 따로 지정하였고 그래프를 구별하기 위해 선의 모양, 색들을 변형해보기도 하였다. 정현파 신호의 기본구성요소인 진동수, 주기, 진폭, 위상 관점에서 문제의 의미를 분석해보았다.



























소개글