광안리 해수욕장 방파제 설계 - 설계파 및 파력 산정, 설계파 산정, 파력 산정

목차

설계파 및 파력 산정


1. 대상지역 : 광안리해수욕장

2. 설계파 자료 및 검색 프로그램 이용

3. 설계파 산정
　(1) 심해파의 파장
　(2) 천수계수 (Ks)
　(3) 굴절 계수(Kr)
　(4) 환산심해파고(H0·´)
　(5) 쇄파고 계산( Goda)

4. 파력산정
　(1) Goda 공식
　(2) Minikin 공식
　(3) Hiroi 공식

본문내용

.0290
1.12
8.96
1.53
12.24
5
275.95
8.25
0.0299
1.11
9.15
1.52
12.54
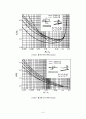
<그림3> 쇄파수심의 변화 (Goda)
<그림4> 쇄파파고의 변화 (Goda)
4. 파력산정
※ 광안리 연안의 수심 10m 지점에 방파제를 설계한다.
방파제는 직립벽이다. ☞ 직립제는 전면 수심과 파고의 관계 (h/H)에 따라서
중복파 또는 쇄파가 작용한다.
h = 10m , H = 8.96m ☞ h / H = 1.12이므로
0.8 < h/H < 2 ☞ 쇄파 파압식 사용
☞ Goda 공식, Minikin 공식, Hiroi 공식
최고조위는 1.56m (국립해양 조사원 http://www.khoa.go.kr/ )
안정계수 1.2
콘크리트와 사석의 마찰계수 0.7
β = 22.5°
d = 6m
h´ = 7+1.56 = 8.56m
hc = 5m
B = 15m
h = 10m
해수의 단위중량 1.024 t/m3
콘크리트의 단위중량 2.5 t/m3
(1) Goda 공식
※ 파봉이 작용
η* =
p1 =
p2 =
p3 =
a1 = {}
a2 = min{}
a3 =
η* : 정수면상 파압강도가 0이 되는 높이(m)
p1 : 정수면상 있어서의 파압강도(t/m2)
p2 : 해저면에 있어서의 파압강도(t/m2)
p3 : 직립벽저면에 있어서의 파압강도(t/m2)
h : 방파제 지점의 수심(m)
hb : 외해로 유의파고의 5배만큼 떨어진 직립벽전면에 있어서의 수심(m)
h´ : 직립벽 저면에 대한 수심(m)
hc : 설계조위면에서의 방파제 천단가지의 높이(m)
d : 근고공 또는 마운드 피복공의 마루 중 작은 수심(m)
w0 : 해수의 단위중량(1.024t/m3)
Hd : 설계계산에 적용된 파고(m)
L : 수심 h에 있어서의 설계계산에 적용된 파장(m)
β : 직립벽법선의 수선과 파의 주방향에서 ±15° 의 범위에서 가장 위험한
방향이되는 각도
η* =
a1 =
a2 = min{} = min(0.217 , 1.34) = 0.217
※
a3 =
※
p1 =
p3 =
직립부에 작용하는 전파압 및 모멘트
- 전파압
P =
P =
p4 =
p4 =
- 전도 모멘트
M =
직립부에 작용하는 전양압력 및 모멘트
Pu =
=
- 전양압력
=
- 모멘트
Mu =
=
※ 안정계수 1.2
콘크리트와 사석의 마찰계수 0.7
※ 방파제의 자중
※ 방파제의 부력
부력 =
γ = 해수의 단위중량
= 1.024 t/m3
V´ = 물에 잠긴 부분의 체적
= 7 × 15 × 1 = 105 m3
부력 = 1.024 × 105 = 107.52 t*m/m
③ 직립부에 작용하는 파력에 대한 안정성
- 직립부에 작용하는 전도 모멘트
M = 724.84 t*m/m
☞ 안전율(1.2) 고려 ☞ 1.2 × 724.84 = 869.81 t*m/m
- 저항모멘트(자중에 의한 M)
Mr = (12×15×1×2.5-107.52)×7.5×0.7 = 1798.02 t*m/m
∴ 869.81 t*m/m < 1798.02 t*m/m 이므로 안정하다.
④ 직립부에 작용하는 양압력에 대한 모멘트
- 하부에 작용하는 모멘트
Mu = 545.3 t*m/m
☞ 안전율(1.2) 고려 ☞ 1.2×545.3 = 654.36 t*m/m
- 저항모멘트(자중에 의한 M)
Mr = (12×15×1×2.5-107.52)×7.5 = 2568.6 t*m/m
∴ 654.36 t*m/m < 2568.6 t*m/m 이므로 안정하다.
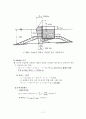
<그림5> Goda의 파봉이 작용할 경우 파압분포도
(2) Minikin 공식
▶ 혼성제 직립벽에 작용하는 쇄파의 파압을 충격압과 정수압으로 분리하여 계산
작용파의 형식 결정
- 2H = 2 × 8.96 = 17.38 m, d = 6m ☞ d < 2H 이므로 쇄파가 작용
- 수심 h=10m, 파장 L = 142.86 m
※ 파장 L 구하기
L0 = 275.95m, h = 10m ☞ h / L0 = 0.0362
☞ 천해파의 파장, 파속 및 파고의 변화 관계 그래프이용
☞ h / L = 0.07 ☞ 10 / L = 0.07 ☞ L = 142.86m
충격파압계산
- 최대충격파압
pm =
- 충격압 p1 =
③ 정수압계산
- 정수압 p2 =
=
④ 충격압과 정수압의 합력
- p1 + p2 = 226.35 t/m
※ P´s = ρgH/2 = 4.59 t/m
⑤ 전도 모멘트
- 충격압 p1의 전도 모멘트
M = p1 × 기준점에서 도심까지의 거리
= 188.55 × 6 = 1131.3 t*m/m
- 정수압 p2의 전도 모멘트
M = p2 × 기준점에서 도심까지의 거리
= 37.80 × 4.22 = 159.52 t*m/m
- 전파압의 전도 모멘트
1131.3 + 159.52 = 1290.82 t*m/m
⑥ 안정성 검토
- 전파압의 전도 모멘트 * 안전율(1.2)
= 1290.82 × 1.2 = 1548.98 t*m/m
- 저항모멘트 Mr
Mr = (12×15×1×2.5 - 107.52)×7.5×0.7 = 1798.02 t*m/m
∴ 1548.98 t*m/m < 1798.02 t*m/m 이므로 안정하다.
= 4.59 t/m
=6m
=4.48m
= 63.13t/m2
=10m
4.22m(도심)
188.55t/m
37.80t/m
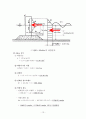
<그림6> Minikin의 파압분포
(3) Hiroi 공식
파압강도
p = 1.5×ρ×g×H
= 1.5×1.024×8.96 = 13.76 t/m2
파압이 0인 지점
1.25H = 1.25 × 8.96 = 11.2 m
③ 전파압
P = (5 + 6) ×1×13.76 = 151.36 t/m
④ 전파압 전도모멘트
M = 151.36 × 6 = 908.16t/m
⑤ 안정성 검토
- 전파압의 전도 모멘트 × 안전율(1.2)
= 908.16 × 1.2 = 1089.79 t/m
- 저항모멘트 Mr
Mr = (12×15×1×2.5 - 107.52)×7.5×0.7 = 1798.02 t*m/m
∴ 1089.79 t*m/m < 1798.02 t*m/m 이므로 안정하다.
<그림7> Hiroi의 파압분포

키워드

광안리,   해수욕장 ,   방파제,   설계,   설계파 ,   파력 산정