양자수

소개글

양자수에 대한 보고서 자료입니다.

본문내용

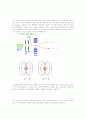
안에 두고, 거기서 나오는 빛의 스펙트럼을 조사하면, 하나뿐이어야 하는 스펙트럼선이 여러 개로 갈라져 보이는 현상.
- 1896년 P.제만이 발견하였는데, 그 중 비교적 간단하게 갈라지는 경우를 정상(正常)제만효과, 복잡하게 갈라지는 경우를 이상(異常)제만효과라고 한다. 정상제만효과는 제만의 스승인 H.A.로렌츠가 발표한 전자론(電子論)으로 설명할 수 있으나, 이상제만효과는 20세기에 들어선 다음에 확립된 양자역학(量子力學)에 의해서 설명될 수 있다. 이상제만효과의 연구를 통해서 소립자가 가지는 기본적인 양으로서 스핀이라는 개념이 탄생하였다
4가지 양자수
http://blog.naver.com/pleades7/120050330720
1.주양자수
n 이라고 나타내며, 전자의 에너지 준위를 나타내는 것으로 n=1,2,3,.... 이며 전자껍질을 나타낸다.
n=1 일때, 전자껍질은 K
n=2 일때, 전자껍질은 L
n=3 일때, 전자껍질은 M
n=4 일때, 전자껍질은 N
n=5 일때, 전자껍질은 O
n=6 일때, 전자껍질은 P
n=7 일때, 전자껍질은 Q
2.방위양자수(부양자수)
l로 표시하며, 전자의 각 운동량을 결정하는 것으로 방위양자수는 부양자수라고도 부르며 오비탈(전자부껍질)의 모양을 결정한다.
l=0,1,2,3.....(n-1) 값을 가져 어떤 전자 껍질에는 그 전자 껍질의 주양자수 만큼 오비탈이 존재하며 오비탈의 기호는 l=0 일때 s, l=1 일때 p, ㅣ=2 일때 d, l=3 일때 f로 표시합니다.
예를들어, n=3 인 M 껍질은 부양자수 l 이 0,1,2 값을 가지므로 s,p,d 의 3가지 오비탈이 존재합니다.
3.자기양자수
m으로 표시하며, 전자구름의 방향과 궤도면의 위치를 결정하는 것으로 m= -l, -l+1, ...0... l-1, l 의 값을 가져 오비탈은 공간배향에 따라 2l+1 개가 존재한다.
예를들어 n=2 인 껍질의 l=1 인 오비탈은 p 이므로 2p로 나타내고, l=1 일때, m은 -1,0,1 의 세방향(x,y,z)의 오비탈이 존재해서 2px,2py,2pz가 존재합니다.
그래서..
s 오비탈은 자기양자수가 0 으로 오비탈 수는 1개 이고,
p 오비탈은 자기양자수가 -1.0.+1 로 오비탈 수는 3개 이고,
d 오비탈은 자기양자수가 -2.-1.0.+1,+2 로 오비탈수는 5개 이고,
f 오비탈은 자기양자수가 -3,-2,-1,0.+1,+2,+3 으로 오비탈 수는 7개가 됩니다.