점성

소개글

점성에 대한 보고서 자료입니다.

목차

점성유체

15.1. 소개

15.2 방정식들

참고 문헌

본문내용

① 점성 ②점성유체 ③점성력
유체 내부에 움직임을 멈추게 하려는 응력이 작용하는 성질
점성의 특성을 갖는 유체
서로 다른 속도로 움직이고 있을 때 균일하게 하려는 응력
어떤 물체에 끈적이는 점도
정지하고 있는 유체 → 응력이 존재하지 않음
운동하고 있는 유체 → (속도기울기가 있을경우)
속도를 평균화해서 균일하게 하려는
접선응력이 나타남.
점성 원인
액체
기체
분자들간의 응집력이 주 원인이며, 온도가 상승하면 점성이 낮아지고
기체는 분자들간의 상호충돌로 인한 운동량 교환이 일어나면서 온도가 상승하면 점성도 증가합니다.
점성
점성계수
점성류
점성유체
점성저항
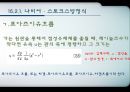
15.1.2. 점성계수
Ex) 유체가 x 축에 평행하게 흘러 속도 u 가 y 방향으로 변화하고 있을 때 y 축에 수직한 면에는
비례상수 μ 가 점성계수가 된다.
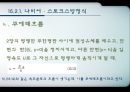
15.1.2. 점성계수
유체의 밀도를 ρ 라고 할 때, 동점성계수 ν
점성유체 속을 움직이는 물체에 작용하는 힘은 점성계수 ρ에 의하지만, 흐름의 상태는 ν인 동점성계수에 의해 지배
15.1.3. 점성류
넓은 의미
점성을 갖는
유체의 층류
좁은 의미
파이프 등을 따라서 압력구배가 있을 때 기체의 흐름~기체분자 끼리의 충돌이 지배적일 때의 압력 하에서의 층류
원형 파이프를 흐르는 점성류는 포아즈이유의 흐름으로써 해석적으로 나타날 수 있다.
원형 이외의 파이프에 대해서는 해석적으로 푸는 일은 곤란하다.
분자류 : 압력이 낮고 기체분자와 파이프 내벽과의 충돌만이
지배적일 경우의 흐름
이 분자류는 분자의 움직임이 문제가 될 정도로 희박한 기체의 흐름을 말함.
15.1.4. 점성유체
점성 유체
운동을 논의할 때 점성을
무시할 수 없는 유체
점성 속도
= 스토크스근사, 오센근사
점성 속도
= 완전유체
15.1.5. 점성저항
속도가 느릴 때에는 점성저항이 크고, 속도가 클수록 압력저항이 커지게 됨.
점성저항은 속도에 비례 , 압력저항은 속도의 제곱에 비례하기 때문.
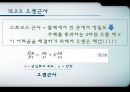
15.2. 방정식들
점성을 가진 유체에 대한 일반적 운동방적이며, 이 방정식을 이용하여 점성이 전혀 없는 완전유체와 관련된 문제부터 경계층의 난류 현상까지 다룰 수 있습니다. 스토크스 법칙은 점성을 가지는 유체 속 에서 낙하운동에 관한 이론인데, 물체가 유체속을 진행할 때 유체분자를 옆으로 밀어내면서 운동량을 전달하기 때문에 물체의 운동을 방해하는 마찰력이 작용하게 됩니다. 이 때 물체의 운동속도가 커질수록 유체내에서의 마찰력인 점성력을 증가시켜 마찰력은 더욱 커지게 됩니다. 수많은 분자의 운동이 관여되기 때문에 거시적인 많은 실험을 통해 통계적으로 결정되어야 합니다. 다음은 오센근사인데,
중략
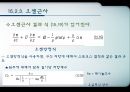
수축하지 않는 유체(incompressible fluid) :
유체의 균형이나 운동을 생각할 때 밀도변화가 무시되는 경우 = 수축하지 않는 유체
밀도변화를 생각할 필요가 있는 유체 = 수축하는 유체 또는 압축성유체
보통 흐름에서는 비압축성유체로 생각. (음속에 비교해서 늦은 운동)

키워드

점성,   유체,   점성유체,   점성력,   유체역학,   역학,   점성응력