정유 체압 Hydrostatic Pressure 실험

소개글

정유 체압 Hydrostatic Pressure 실험에 대한 보고서 자료입니다.

본문내용

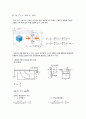
값을 구한다. 앞서 말했듯, 추에 의한 모멘트 M은 다음과 같다. .
이제, 물에 의한 모멘트를 구해보자. 물에 의해 단면이 받는 힘은 앞서 예비보고서를 참고하면 다음과 같다. . 이때 Xct가 바로 r이다. 위에서와 같은 방식으로 방정식을 세운다. 이번에는 Xc를 구하는 방법이 위에서와 다르다.
위 데이터 값을 대입하면 r에 대한 1차 방정식을 얻을 수 있다. 추의 질량을 변화시킴에 따라 달라지는 r값을 표 2에 기록했다.
표를 완성하고 나서 실험 결과에 대해 돌아보았더니 오차율이 10% 미만으로 형성되었다. 계산기를 사용하며 3차 방정식을 해결할 때 혹시 이론값과 측정값 사이의 오차가 매우 크지 않을까 염려했지만 그런 일은 일어나지 않았다. 비교적 정확하게 실험이 진행되었다고 할 수 있을 것이다.
Discussion
1. Confirm that the center of pressure is below the center of area, and discuss why.
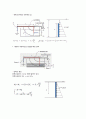
center of pressure (total immersion)
실험 참고자료에 의하면
z= bd³/12 / bd(r-d/2) + (r-d/2) from water surface.
= 0.00083/(r-0.05) + (r-0.05)
이 z값이 바로 center of pressure이 된다.
반면 center point of area => r-d/2 로 나타낼 수 있다.
비교해보면
자연스레 z> r-d/2 임을 알 수가 있다.
따라서 center of pressure 이 center point of area의 아래에 위치한다는 것을 알 수 있다.
그 이유를 추측해보건대
여기서 p₁이 깊이에 따라 일정하게 작용하는 것이 아니라 물의 깊이가 깊어질수록 더 크게 작용하기 때문에, 모멘트 적분을 해보면 압력의 중심이 하단에 작용하게 되는 것을 알 수 있다.
2. Compare the theoretical value with measured length, discuss why does the difference occurs.
이론값과 측정값이 근소한 차이이지만 오차를 내포하고 있다. 오차율이 1%안쪽으로 나오는 것이 매우 정확한 실험이라고 할 수 있겠지만 그러지 못했던 것은 사람 손으로 직접 실험했기 때문이다. 우선 저울이 수평을 이루었는지를 정확하게 맞추는 것이 사실상 불가능하다. 또한 물의 눈금을 읽는 것에도 사람 눈이 정확하지 않기 때문에 그 부분에서 약간의 오차가 발생할 수 있다.
물이 계속 흔들렸던 것도 저울의 수평에 약간의 영향을 주지 않았을까 추측해본다. 물을 확 붓고 확 빼는 과정에서 물이 다소 많이 흔들렸는데 시간이 지나서 겉보기에는 잔잔하지만 아직 물 내무의 흐름이 존재했을 수 있다. 만일 그랬다면 그것은 이 실험의 가정과는 다른 상황이 되어 오차의 원인이 될 수 있다.
마지막으로 처음 수평을 맞출 때 오차가 있었을 것이고 그 오차 역시 실험의 오차 발생에 기여를 했을 것이다.
3. Discuss why we do not consider the pressure at the surface of arc. Why we just calculate the pressure of the rectangular section?
부채꼴 모양의 단면의 경우 이 단면은 반대쪽에도 존재하기 때문에 안쪽과 바깥쪽에서 발생하는 수압이 서로 상쇄 작용을 하여 고려하지 않았다고 생각한다. 정유체에서 힘의 평형을 고려할 때 수평 방향의 힘은 서로 상쇄되어서 없어진다.
다른 곡면에서는 모멘트가 pivot에 의해 어떤 상황에서든 0을 나타내기 때문에 결국 직사각형 단면만 고려하면 된다는 결론에 도달하게 된다.

키워드

정유체압 Hydrostatic Pressure 실험,   Xct값 추출,   ● 유체 정역학