목차
1. 바빌로니아 수학이란
1)발견
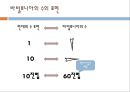
2)수의 표현
3)연습문제
2. 바빌로니아 수학의 특징
1)상업과 농업수학
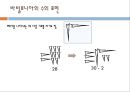
2)기하학
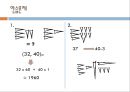
3)대수
4)플림프톤322
1)발견
2)수의 표현
3)연습문제
2. 바빌로니아 수학의 특징
1)상업과 농업수학
2)기하학
3)대수
4)플림프톤322
본문내용
바빌로니아 수학 [바빌로니아 수학 발견, 바빌로니아 수학 수의 표현, 바빌로니아 수학 특징, 바빌로니아 상업 수학, 바빌로니아 농업 수학, 바빌로니아 기하학, 바빌로니아 대수, 바빌로니아 플림프톤322].pptx
바빌로니아 수학
바빌로니아 수학이란
바빌로니아 수학의 발견
╋━━━━━━━━━━─────────
≪ 지 도 ≫
≪ 사 진 ≫
해석하려는 노력 X
바빌로니아 수학의 발견
╋━━━━━━━━━━─────────
≪ 사 진 ≫
≪ 그 림 ≫
헨리 롤린슨(1810~1895)
1846년 페르시아로 파견된
영국의 외교관 헨리롤린슨이
베이스툰(현 이란 비시툰)의
한 절벽에서 높이7m폭18m의
비문을 발견
≪ 그 림 ≫
바빌로니아 수학의 발견
╋━━━━━━━━━━─────────
□ 쐐기문자의 해독 덕에 점토판의 해석이 가능해졌고 그로 인해 당시의 생활상과 지식 등을 알 수 있게 되었다.
□ 오늘 날 우리가 배우고 있는 기하학, 대수 등 의 여러 수학적 지식들은 이를 통해 알려진 것들이다.
바빌로니아 수학
바빌로니아 수학이란
바빌로니아 수학의 발견
╋━━━━━━━━━━─────────
≪ 지 도 ≫
≪ 사 진 ≫
해석하려는 노력 X
바빌로니아 수학의 발견
╋━━━━━━━━━━─────────
≪ 사 진 ≫
≪ 그 림 ≫
헨리 롤린슨(1810~1895)
1846년 페르시아로 파견된
영국의 외교관 헨리롤린슨이
베이스툰(현 이란 비시툰)의
한 절벽에서 높이7m폭18m의
비문을 발견
≪ 그 림 ≫
바빌로니아 수학의 발견
╋━━━━━━━━━━─────────
□ 쐐기문자의 해독 덕에 점토판의 해석이 가능해졌고 그로 인해 당시의 생활상과 지식 등을 알 수 있게 되었다.
□ 오늘 날 우리가 배우고 있는 기하학, 대수 등 의 여러 수학적 지식들은 이를 통해 알려진 것들이다.










































소개글