목차
데이터 분석표 - A1: 발사속도
Part A1 & Part A2: 결론/질문
PART B: 결론/질문
데이터 분석표 - C1: 측정거리
오차율
오차분석
결과분석
Part A1 & Part A2: 결론/질문
PART B: 결론/질문
데이터 분석표 - C1: 측정거리
오차율
오차분석
결과분석
본문내용
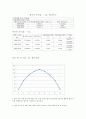
(v2)sin2θ/g 입니다.
v가 동일할 때 s가 가장 클 경우는 sin2θ가 가장 클 때이고 sin은 사잇각이 90°
일 때 2θ = 90° 즉 사잇각(θ)이 45° 일 대 가장 멀리 날아간다.
(Y축 단위: cm)
7. 오차율이 가장 적은 것으로 보아 45°에서 발사하는 것이 가장 정확하다.
데이터 분석표 - C1: 측정거리
높이: 0.805m
두 포트게이트 간의 거리: 0.1m
각(°)
두 포트게이트 사이를 지나는 시간 (s)
비행 시간 (s)
수평 거리[m(측정)]
-20°
0.0313 s
0.2910s
0.87m
-10°
0.0315 s
0.3355s
1.02m
10
0.0326 s
0.4553s
1.38m
데이터 분석표 - C2: 발사 속도, 계산 거리
각(°)
발사 속도(m/s)
수평 거리[m(계산)]
오차율(%)
-20°
3.194m/s
0.92m
0.000574712%
-10°
3.174m/s
1.06m
0.000392156%
10°
3.067m/s
1.39m
0.000072463%
PART C: 결론/질문
오차율
데이터 분석표 - A2
딸깍 소리의 횟수
오차율(%)
3번째 딸깍
2.85m-2.06m/2.85x100m=0.002771929%
2번째 딸깍
1.65m-1.58m/1.65x100m=0.000424242%
1번째 딸깍
1.27m-1.21m/1.27x100m=0.00047244%
데이터 분석표 - B2
각(°)
오차율(%)
25°
0.82m-0.81m/0.82x100m=0.000121951%
35°
0.96m-0.95m/0.96x100m=0.000104166%
45°
1.03m-1.02m/1.03x100m=0.000097087%
55°
1.01m-1.00m/1.01x100m=0.000099009%
65°
0.87m-0.86m/0.87x100m=0.000114942%
75°
0.66m-0.65m/0.65x100m=0.000151515%
데이터 분석표 - C2
각(°)
오차율(%)
-20°
|0.87m-0.92m/0.87x100m|=0.000574712%
-10°
|1.02m-1.06m/1.02x100m|=0.000392156%
10°
|1.38m-1.39m/1.28x100m|=0.000072463%
오차분석
공기 저항을 존재하지 않는다는 가정 하에 실험을 진행했다. 그렇기에 실제로는 공기 저항이 있음에 따라 오차가 발생하였다.
공이 발사대에서 발사할 때 발생한 마찰력을 고려하지 못했다.
결과분석
각도에 따라 거리가 변하는 이유는 마찰이 없을 경우 45° 이하일 때 중력으로 인해 비행거리 자체가 짧았다가 45°에 가까이 갈수록 커지며 도달거리가 길어지고, 45° 이상의 경우 각도가 이상적인 각도인 45°에서 멀어짐에 따라 너무 높은 각도로 인하여 상하이동에 힘을 너무 많이 쓰게 되어 실제 수평거리 자체는 짧고 위와 마찬가지로 경계인 45°에서 멀어질수록 줄어드는 것을 볼 수 있다. 공기 저항의 요인으로 45° 나오지 않을 거라고 생각했으나 실험 후 가장 멀리가는 각도가 45°가 되는 것을 보고 조금 의아했다.
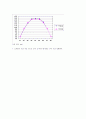
v가 동일할 때 s가 가장 클 경우는 sin2θ가 가장 클 때이고 sin은 사잇각이 90°
일 때 2θ = 90° 즉 사잇각(θ)이 45° 일 대 가장 멀리 날아간다.
(Y축 단위: cm)
7. 오차율이 가장 적은 것으로 보아 45°에서 발사하는 것이 가장 정확하다.
데이터 분석표 - C1: 측정거리
높이: 0.805m
두 포트게이트 간의 거리: 0.1m
각(°)
두 포트게이트 사이를 지나는 시간 (s)
비행 시간 (s)
수평 거리[m(측정)]
-20°
0.0313 s
0.2910s
0.87m
-10°
0.0315 s
0.3355s
1.02m
10
0.0326 s
0.4553s
1.38m
데이터 분석표 - C2: 발사 속도, 계산 거리
각(°)
발사 속도(m/s)
수평 거리[m(계산)]
오차율(%)
-20°
3.194m/s
0.92m
0.000574712%
-10°
3.174m/s
1.06m
0.000392156%
10°
3.067m/s
1.39m
0.000072463%
PART C: 결론/질문
오차율
데이터 분석표 - A2
딸깍 소리의 횟수
오차율(%)
3번째 딸깍
2.85m-2.06m/2.85x100m=0.002771929%
2번째 딸깍
1.65m-1.58m/1.65x100m=0.000424242%
1번째 딸깍
1.27m-1.21m/1.27x100m=0.00047244%
데이터 분석표 - B2
각(°)
오차율(%)
25°
0.82m-0.81m/0.82x100m=0.000121951%
35°
0.96m-0.95m/0.96x100m=0.000104166%
45°
1.03m-1.02m/1.03x100m=0.000097087%
55°
1.01m-1.00m/1.01x100m=0.000099009%
65°
0.87m-0.86m/0.87x100m=0.000114942%
75°
0.66m-0.65m/0.65x100m=0.000151515%
데이터 분석표 - C2
각(°)
오차율(%)
-20°
|0.87m-0.92m/0.87x100m|=0.000574712%
-10°
|1.02m-1.06m/1.02x100m|=0.000392156%
10°
|1.38m-1.39m/1.28x100m|=0.000072463%
오차분석
공기 저항을 존재하지 않는다는 가정 하에 실험을 진행했다. 그렇기에 실제로는 공기 저항이 있음에 따라 오차가 발생하였다.
공이 발사대에서 발사할 때 발생한 마찰력을 고려하지 못했다.
결과분석
각도에 따라 거리가 변하는 이유는 마찰이 없을 경우 45° 이하일 때 중력으로 인해 비행거리 자체가 짧았다가 45°에 가까이 갈수록 커지며 도달거리가 길어지고, 45° 이상의 경우 각도가 이상적인 각도인 45°에서 멀어짐에 따라 너무 높은 각도로 인하여 상하이동에 힘을 너무 많이 쓰게 되어 실제 수평거리 자체는 짧고 위와 마찬가지로 경계인 45°에서 멀어질수록 줄어드는 것을 볼 수 있다. 공기 저항의 요인으로 45° 나오지 않을 거라고 생각했으나 실험 후 가장 멀리가는 각도가 45°가 되는 것을 보고 조금 의아했다.


























소개글