실린더 주위의 유체유동측정 유체역학, 레이놀즈수

소개글

실린더 주위의 유체유동측정 유체역학, 레이놀즈수에 대한 보고서 자료입니다.

목차

1. 목 적
2. 이 론
3.에디슨에 따른 시뮬레이션 유동해석

본문내용

비이다. 이 수는 유체의 밀도, 흐름의 속도, 흐름속에 있는 물체의 길이가 클수록 커지고, 유체의 점성률에는 반비례한다. 영국의 공학자 레이놀즈 가 도입한것이다.
reynoldsnmber = 관성력 / 점성력
층류에서 난류로 , 또는 난류에서 층류로 천이할때의 유속을 임계속도라고 하고, 그 때의 레이놀즈 수를 임계레이놀즈수라고 한다. 층류에서 난류로 바뀔 때의 레이놀즈 수의 값을 상임계레이놀즈수라고하고, 난류에서 층류로 바뀔때의 레이놀즈 수를 하임계레이놀즈 수라고 한다.
3.에디슨에 따른 시뮬레이션 유동해석
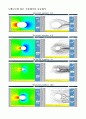
Reynold number 0.5
Reynold number 4.0
Reynold number 10
Reynold number 100
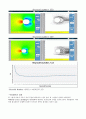
Reynold number 250
Reynold number 500
-Reynold Number 범위(10~490)(단위 10)
-시뮬레이션 결과
위 그림에 나타나 잇듯이 공의 주변의 압력차이가 생겨 난다. 위 그림들은 물체의 아랫면에서
와류흘림 (vortex shedding)이 발생할때에 형성되는 유동흐름의 양상을 보여주고있다. 와류흘림이 아래쪽에 형성되면서 아래쪽의 압력이 증가되어 양력이 발생되는 원인이 된다.

키워드

레이놀드수,   레이놀즈수,   reynold number,   유체역학,   실린더