본문내용
1.5000
1.4844
0.0179
1.051
8
1.4688
1.4844
1.4766
-0.0034
0.528
9
1.4766
1.4844
1.4805
0.0073
0.263
10
1.4766
1.4805
1.4785
0.0019
0.135
11
1.4766
1.4785
1.4775
-0.0007
0.068
False-position of Bracketing method
function y = han3(x);
y = x^2 - 0.2333*x - 1.8391221;
end
>>falsi('han3', 0, 2, 0.001, 50)
Bisect법과 거의 비슷하게 오차가 줄어들고 있는 경향을 보이는데 중간에 꺽어진 부분은 오차가 급격히 줄어드는 현상이다.
Iteration
Brackets
Estimate
y
1
0
2.0000
1.0410
-0.9983
ㆍ
2
1.0410
2.0000
1.3966
-0.2146
25.462
3
1.3966
2.0000
1.4644
-0.0363
4.630
4
1.4644
2.0000
1.4756
-0.0059
0.759
5
1.4756
2.0000
1.4775
-0.0010
0.129
6
1.4775
2.0000
1.4777
-0.0002
0.014
Newton-Raphson of Open method
function y = han5(x);
y = 0;
y = 2*x - 0.2333;
end
>>newton('han3', 'han5', 3, 0.001, 50)
False-position과 마찬가지로 꺽이는 부분이 존재하므로 오차가 근에 갈수록 급격히 줄어든다.
Iteration
y
1
3.0000
6.4610
ㆍ
2
1.8796
1.2553
59.608
3
1.5236
0.1267
23.366
4
1.4785
0.0020
3.050
5
1.4778
0.0000
0.047
Secant of Open method
function y = han3(x);
y = x^2 - 0.2333*x - 1.8391221;
end
>>secant('han3', 0, 2, 0.001, 50)
첫 부분에 보이는 그래프의 기울기가 직선의 모습을 한 형태는 오차가 100%인 지점이다. Secant도 결국 근에 근접할수록 오차가 줄어든다.
Iteration
y
1
0
-1.8391
ㆍ
2
2.0000
1.6943
100.000
3
1.0410
-0.9983
92.123
4
1.3966
-0.2146
25.462
5
1.4939
0.0441
6.513
6
1.4773
-0.0013
1.124
7
1.4778
-0.0000
0.034
Muller of Open method
function y = han3(x);
y = x^2 - 0.2333*x - 1.8391221;
end
>>muller('han3', 0, 2, 0.001, 50)
그래프의 첫 부분에서 오차가 100%로 y=c의 형태가 나타났고 Iteration 3에서 근으로 수렴하므로 오차가 0이 된다.
Iteration
y
1
0
-1.8391
ㆍ
2
2.0000
1.6943
100.000
3
1.0000
-1.0724
100.000
4
1.4778
0
32.332
5
1.4778
0
0.000
Fixed-point iteration method
function y = han6(x);
y = 0;
y = x.^2 - 0.2333.*x - 1.8391221 + x;
end
>>fixed_pt_sys('han6', 0, 0.001, 50)
그래프에서 오차의 폭이 커졌다가 작아지는 것을 반복하고 있다. 이는 Fixed-point iteration method의 특징이다. 그렇게 오차의 폭이 변하다가 결국은 수렴하게 된다. 즉, 근이 구해졌다.
Iteration
y
1
-1.8391
1.8391
ㆍ
2
0.1332
1.9723
1480.706
3
-1.7193
1.8525
107.747
4
-0.2014
1.5178
753.674
5
-1.9530
1.7516
89.688
6
0.4777
2.4306
508.834
7
-1.2447
1.7224
138.379
8
-1.2441
0.0007
0.048
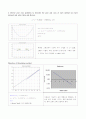
Bracketing methods
Open methods
Bisection
False-position
Newton-Raphson
Secant
Muller
Fixed-point
반복 횟수
11
6
5
7
5
8
정확도
-0.0007
-0.0002
0.0000
-0.0000
0.0000
0.0007
구해진 근
1.4775
1.4777
1.4778
1.4778
1.4778
-1.2441(X)
위 1번 문제가 거의 유사한 결과를 가져왔다.
일단 위 식 , x>0에서 근을 구하는 방법 중 가장 좋은 것은 Muller법이라고 여겨진다. Muller법은 다른 방법들보다 반복 횟수도 1∼6회가 적었으며 오차도 거의 없었다. 물론 컴퓨터 계산상의 오차가 약간은 있을 수 있지만 허용오차를 0.001로 잡았기 때문에 거의 없다고 봐도 무방했다.
Bisection법 같은 경우 반복 횟수도 제일 많고 정확도도 제일 떨어졌다. 그리고 False-position법 같은 경우 반복 횟수는 적었으나 오차가 약간 발생하였고 이 두 방법은 근을 포함하고 있는 구간을 잡아야 하는 번거로움이 있기 때문에 좋은 방법이 될 수 없을 것 같다.
Newton-Raphson법 같은 경우 오차는 거의 없었고 반복 횟수도 적었지만, 식을 미분하여 입력해야 하는 번거로움이 있어 그 과정동안 계산상의 오류가 생길 수 있기 때문에 좋은 방법은 아닌듯 하다. Secant법 같은 경우도 Muller법보다 반복 횟수가 많았다.
따라서 가장 효율적인 근을 구하는 방법은 Muller법으로 여겨진다.
Fixed-point iteration method법 같은 경우엔 처음 출발 값을 0과 5를 잡았는데 0에서 출발한 값은 음의 근을 구하였다. 하지만 문제에서 x<0이란 초기 조건을 걸었기 때문에 이것은 근이 될 수 없다. 그리고 5에서 출발한 값은 근에 수렴하지 못하고 발산 하였다. 따라서 이 식에서는 Fixed-point iteration method법을 적용하지는 못할 것 같다.
1.4844
0.0179
1.051
8
1.4688
1.4844
1.4766
-0.0034
0.528
9
1.4766
1.4844
1.4805
0.0073
0.263
10
1.4766
1.4805
1.4785
0.0019
0.135
11
1.4766
1.4785
1.4775
-0.0007
0.068
False-position of Bracketing method
function y = han3(x);
y = x^2 - 0.2333*x - 1.8391221;
end
>>falsi('han3', 0, 2, 0.001, 50)
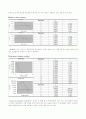
Bisect법과 거의 비슷하게 오차가 줄어들고 있는 경향을 보이는데 중간에 꺽어진 부분은 오차가 급격히 줄어드는 현상이다.
Iteration
Brackets
Estimate
y
1
0
2.0000
1.0410
-0.9983
ㆍ
2
1.0410
2.0000
1.3966
-0.2146
25.462
3
1.3966
2.0000
1.4644
-0.0363
4.630
4
1.4644
2.0000
1.4756
-0.0059
0.759
5
1.4756
2.0000
1.4775
-0.0010
0.129
6
1.4775
2.0000
1.4777
-0.0002
0.014
Newton-Raphson of Open method
function y = han5(x);
y = 0;
y = 2*x - 0.2333;
end
>>newton('han3', 'han5', 3, 0.001, 50)
False-position과 마찬가지로 꺽이는 부분이 존재하므로 오차가 근에 갈수록 급격히 줄어든다.
Iteration
y
1
3.0000
6.4610
ㆍ
2
1.8796
1.2553
59.608
3
1.5236
0.1267
23.366
4
1.4785
0.0020
3.050
5
1.4778
0.0000
0.047
Secant of Open method
function y = han3(x);
y = x^2 - 0.2333*x - 1.8391221;
end
>>secant('han3', 0, 2, 0.001, 50)
첫 부분에 보이는 그래프의 기울기가 직선의 모습을 한 형태는 오차가 100%인 지점이다. Secant도 결국 근에 근접할수록 오차가 줄어든다.
Iteration
y
1
0
-1.8391
ㆍ
2
2.0000
1.6943
100.000
3
1.0410
-0.9983
92.123
4
1.3966
-0.2146
25.462
5
1.4939
0.0441
6.513
6
1.4773
-0.0013
1.124
7
1.4778
-0.0000
0.034
Muller of Open method
function y = han3(x);
y = x^2 - 0.2333*x - 1.8391221;
end
>>muller('han3', 0, 2, 0.001, 50)
그래프의 첫 부분에서 오차가 100%로 y=c의 형태가 나타났고 Iteration 3에서 근으로 수렴하므로 오차가 0이 된다.
Iteration
y
1
0
-1.8391
ㆍ
2
2.0000
1.6943
100.000
3
1.0000
-1.0724
100.000
4
1.4778
0
32.332
5
1.4778
0
0.000
Fixed-point iteration method
function y = han6(x);
y = 0;
y = x.^2 - 0.2333.*x - 1.8391221 + x;
end
>>fixed_pt_sys('han6', 0, 0.001, 50)
그래프에서 오차의 폭이 커졌다가 작아지는 것을 반복하고 있다. 이는 Fixed-point iteration method의 특징이다. 그렇게 오차의 폭이 변하다가 결국은 수렴하게 된다. 즉, 근이 구해졌다.
Iteration
y
1
-1.8391
1.8391
ㆍ
2
0.1332
1.9723
1480.706
3
-1.7193
1.8525
107.747
4
-0.2014
1.5178
753.674
5
-1.9530
1.7516
89.688
6
0.4777
2.4306
508.834
7
-1.2447
1.7224
138.379
8
-1.2441
0.0007
0.048
Bracketing methods
Open methods
Bisection
False-position
Newton-Raphson
Secant
Muller
Fixed-point
반복 횟수
11
6
5
7
5
8
정확도
-0.0007
-0.0002
0.0000
-0.0000
0.0000
0.0007
구해진 근
1.4775
1.4777
1.4778
1.4778
1.4778
-1.2441(X)
위 1번 문제가 거의 유사한 결과를 가져왔다.
일단 위 식 , x>0에서 근을 구하는 방법 중 가장 좋은 것은 Muller법이라고 여겨진다. Muller법은 다른 방법들보다 반복 횟수도 1∼6회가 적었으며 오차도 거의 없었다. 물론 컴퓨터 계산상의 오차가 약간은 있을 수 있지만 허용오차를 0.001로 잡았기 때문에 거의 없다고 봐도 무방했다.
Bisection법 같은 경우 반복 횟수도 제일 많고 정확도도 제일 떨어졌다. 그리고 False-position법 같은 경우 반복 횟수는 적었으나 오차가 약간 발생하였고 이 두 방법은 근을 포함하고 있는 구간을 잡아야 하는 번거로움이 있기 때문에 좋은 방법이 될 수 없을 것 같다.
Newton-Raphson법 같은 경우 오차는 거의 없었고 반복 횟수도 적었지만, 식을 미분하여 입력해야 하는 번거로움이 있어 그 과정동안 계산상의 오류가 생길 수 있기 때문에 좋은 방법은 아닌듯 하다. Secant법 같은 경우도 Muller법보다 반복 횟수가 많았다.
따라서 가장 효율적인 근을 구하는 방법은 Muller법으로 여겨진다.
Fixed-point iteration method법 같은 경우엔 처음 출발 값을 0과 5를 잡았는데 0에서 출발한 값은 음의 근을 구하였다. 하지만 문제에서 x<0이란 초기 조건을 걸었기 때문에 이것은 근이 될 수 없다. 그리고 5에서 출발한 값은 근에 수렴하지 못하고 발산 하였다. 따라서 이 식에서는 Fixed-point iteration method법을 적용하지는 못할 것 같다.





































소개글