본문내용
txt","w");
fprintf(out,"variable=x,y\n\n");
for(i=0;i<=NM-1;i++)
{
fprintf(out,"\nzone t=\"t=%3.4f\",j=41\n",i*0.002);
for(j=0;j<=JM-1;j++)
{
fprintf(out,"%3.4lf\t%2.1f\n",U[i][j],j*0.1);
}
}
fclose(out);
}
2) 각 방법 결과를 Tecplot으로 시간을 0.24간격(120)
(1) FTCS Method
(2) Dufort-Frankel Method
(3) Lassonen Method
(4) Crank-Nicolson Method
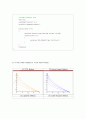
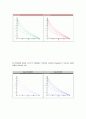
3) FTCS법에 대하여 시간간격 0.00232로 변경하여 산출하여 Tecplot으로 나타내고 0.002일때와 비교하여 서술
del_t=0.00232
del_t=0.002
4) 고 찰
두 평판 사이에 흐르는 유체에 대한 속도 분포를 C++을 이용하여 Explicit Method (양함수법)인 FTCS Method, Dufort-Frankel Method과 Implicit Method (음함수법)인 Lassonen Method, Crank-Nicolson Method을 이용하여 각 각 출력값의 차이를 비교해 보았다.
먼저 Explicit Method(양함수법)인 FTCS와 Dufort-Frankel을 비교해 보았을 때 FTCS Method이 다른 방법보다는 자세한 출력값을 보였다. 두 번째로 Implicit Method(음함수법)인 Lassonen과 Crank-Nicolson을 비교한 경우에는 큰 차이가 없었다. 세 번째로 Explicit Method과 Implicit Method을 비교한 경우는 확실히 양함수법보다 음함수법이 두 평판사이에 흐르는 유체의 속도분포가 자세히 출력이 되었다. 양함수법에서는 전진 차분 형식(Forward difference form)으로 나타나고, 음학수법에서는(Backward difference form)으로 나타난다. 그리고 양함수법은 적용하기 쉽지만 해를 구하는 과정에서 불안정성을 피하기 위해 시간 단계에 제한을 두어햐 하고, 음함수법은 본래 안정적이고, 시간 단계로서 djEJs 값의 △t의 최대값은 안정성 기준에 의해 제한된다. △t의 최대값은 최소 기본 계수를 이용하여 방정식에 안정성 기준을 적용하면 구할 수 있는데, 이것은 최소 기본 계수가 가장 제한적이기 때문이며 각 시간 단계에 대하여 절점의 속도들을 동시에 연립적으로 풀어야 하지만 시간 단계의 크기에 제한이 없다는 장단점이 있다.
그리고 C++을 이용하면서 4가지 Method으로 프로그래밍을 하면서 양함수법은 별 어려움이 없이 하였지만 음함수법에서 배열을 선언한 다음에 계수를 결정하는데 많은 어려움이 있었다.
Report 2
1) Jacobi Method
#include
#include
#define x 1
#define y 2
#define del_x 0.05
#define del_y 0.05
#define NM 21
#define JM 41
#define err_max 0.01
void main()
{
int i,j;
int n=1;
double err;
double T[NM][JM];
double old_T[NM][JM];
double fabs(double);
//Matrix 초기화
for(i=0;i<=NM-1;i++)
{
for(j=0;j<=JM-1;j++)
{
T[i][j]=0;
}
}
//Initial condition
for(i=0;i<=NM-1;i++)
{
T[i][0]=100;
T[i][40]=0;
}
for(j=1;j<=JM-2;j++)
{
T[0][j]=0;
T[20][j]=0;
}
//조건을 만족 할 때까지 루프반복
do
{
n=n++;
err=0;
for(i=0;i<=NM-1;i++)
{
for(j=0;j<=JM-1;j++)
{
old_T[i][j]=T[i][j];
}
}
for(i=1;i<=19;i++)
{
for(j=1;j<=39;j++)
{
T[i][j]=(old_T[i+1][j]+old_T[i-1][j]+old_T[i][j+1]+old_T[i][j-1])/4;
err=err+fabs(T[i][j]-old_T[i][j]);
}
}
}
while (err_max
FILE*out;
out=fopen("Jacobi.txt","w");
fprintf(out,"variables=x,y,T\nzone i=21,j=41,f=point\n\n");
printf("iteration = %d\n",n-1);
for(i=0;i<=NM-1;i++)
{
for(j=0;j<=JM-1;j++)
{
fprintf(out,"%3.2f\t%3.2f\t%3.2f\n",del_x*i,del_y*j,old_T[i][j]);
}
}
fclose(out);
}
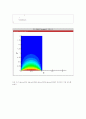
2) 결과를 Tecplot로 그릴 것
처음 조건 del_x=0.05, del_y=0.05을 del_x=0.025 del_y=0.025로 변경하여 색을 밀도를
높였다
3) Error_max 값이 0.01,0.001일 경우 Interation 수 산출
Error_max=0.01
Error_max=0.001
Error가 Error_max값보다 작아질때까지 루프를 반복한 횟수는 Error_max가 0.01일 때는 Interation이 1076이 나왔으면 Error_max가 0.001일 때는 Interation이가 1374가 나왔다.
4) 고 찰
Jacobi Method은 안정화 조건 없이 해를 구할 수 있으며 코딩에서 초기 조건과 경계 조건을 주고 Jacobi Function을 써서 결과 값을 얻을 수 있었다.
Tecplot를 이용하여 2차원 상에 가로 1 세로 2인 직사각형 내부의 온도 분포를 관찰할 수 있었다. 열전달에서 Analytical-Method 방법을 직접 손으로 풀던 문제를 프로그램을 이용하여 쉽게 값을 얻을 수 있었다.
늦게 제출하여서 죄송합니다. 보기에는 미흡하시지만 혼자서 Tecplot Program을 하면서 많을 것을 배우는 계기가 되었습니다.
fprintf(out,"variable=x,y\n\n");
for(i=0;i<=NM-1;i++)
{
fprintf(out,"\nzone t=\"t=%3.4f\",j=41\n",i*0.002);
for(j=0;j<=JM-1;j++)
{
fprintf(out,"%3.4lf\t%2.1f\n",U[i][j],j*0.1);
}
}
fclose(out);
}
2) 각 방법 결과를 Tecplot으로 시간을 0.24간격(120)
(1) FTCS Method
(2) Dufort-Frankel Method
(3) Lassonen Method
(4) Crank-Nicolson Method
3) FTCS법에 대하여 시간간격 0.00232로 변경하여 산출하여 Tecplot으로 나타내고 0.002일때와 비교하여 서술
del_t=0.00232
del_t=0.002
4) 고 찰
두 평판 사이에 흐르는 유체에 대한 속도 분포를 C++을 이용하여 Explicit Method (양함수법)인 FTCS Method, Dufort-Frankel Method과 Implicit Method (음함수법)인 Lassonen Method, Crank-Nicolson Method을 이용하여 각 각 출력값의 차이를 비교해 보았다.
먼저 Explicit Method(양함수법)인 FTCS와 Dufort-Frankel을 비교해 보았을 때 FTCS Method이 다른 방법보다는 자세한 출력값을 보였다. 두 번째로 Implicit Method(음함수법)인 Lassonen과 Crank-Nicolson을 비교한 경우에는 큰 차이가 없었다. 세 번째로 Explicit Method과 Implicit Method을 비교한 경우는 확실히 양함수법보다 음함수법이 두 평판사이에 흐르는 유체의 속도분포가 자세히 출력이 되었다. 양함수법에서는 전진 차분 형식(Forward difference form)으로 나타나고, 음학수법에서는(Backward difference form)으로 나타난다. 그리고 양함수법은 적용하기 쉽지만 해를 구하는 과정에서 불안정성을 피하기 위해 시간 단계에 제한을 두어햐 하고, 음함수법은 본래 안정적이고, 시간 단계로서 djEJs 값의 △t의 최대값은 안정성 기준에 의해 제한된다. △t의 최대값은 최소 기본 계수를 이용하여 방정식에 안정성 기준을 적용하면 구할 수 있는데, 이것은 최소 기본 계수가 가장 제한적이기 때문이며 각 시간 단계에 대하여 절점의 속도들을 동시에 연립적으로 풀어야 하지만 시간 단계의 크기에 제한이 없다는 장단점이 있다.
그리고 C++을 이용하면서 4가지 Method으로 프로그래밍을 하면서 양함수법은 별 어려움이 없이 하였지만 음함수법에서 배열을 선언한 다음에 계수를 결정하는데 많은 어려움이 있었다.
Report 2
1) Jacobi Method
#include
#include
#define x 1
#define y 2
#define del_x 0.05
#define del_y 0.05
#define NM 21
#define JM 41
#define err_max 0.01
void main()
{
int i,j;
int n=1;
double err;
double T[NM][JM];
double old_T[NM][JM];
double fabs(double);
//Matrix 초기화
for(i=0;i<=NM-1;i++)
{
for(j=0;j<=JM-1;j++)
{
T[i][j]=0;
}
}
//Initial condition
for(i=0;i<=NM-1;i++)
{
T[i][0]=100;
T[i][40]=0;
}
for(j=1;j<=JM-2;j++)
{
T[0][j]=0;
T[20][j]=0;
}
//조건을 만족 할 때까지 루프반복
do
{
n=n++;
err=0;
for(i=0;i<=NM-1;i++)
{
for(j=0;j<=JM-1;j++)
{
old_T[i][j]=T[i][j];
}
}
for(i=1;i<=19;i++)
{
for(j=1;j<=39;j++)
{
T[i][j]=(old_T[i+1][j]+old_T[i-1][j]+old_T[i][j+1]+old_T[i][j-1])/4;
err=err+fabs(T[i][j]-old_T[i][j]);
}
}
}
while (err_max
FILE*out;
out=fopen("Jacobi.txt","w");
fprintf(out,"variables=x,y,T\nzone i=21,j=41,f=point\n\n");
printf("iteration = %d\n",n-1);
for(i=0;i<=NM-1;i++)
{
for(j=0;j<=JM-1;j++)
{
fprintf(out,"%3.2f\t%3.2f\t%3.2f\n",del_x*i,del_y*j,old_T[i][j]);
}
}
fclose(out);
}
2) 결과를 Tecplot로 그릴 것
처음 조건 del_x=0.05, del_y=0.05을 del_x=0.025 del_y=0.025로 변경하여 색을 밀도를
높였다
3) Error_max 값이 0.01,0.001일 경우 Interation 수 산출
Error_max=0.01
Error_max=0.001
Error가 Error_max값보다 작아질때까지 루프를 반복한 횟수는 Error_max가 0.01일 때는 Interation이 1076이 나왔으면 Error_max가 0.001일 때는 Interation이가 1374가 나왔다.
4) 고 찰
Jacobi Method은 안정화 조건 없이 해를 구할 수 있으며 코딩에서 초기 조건과 경계 조건을 주고 Jacobi Function을 써서 결과 값을 얻을 수 있었다.
Tecplot를 이용하여 2차원 상에 가로 1 세로 2인 직사각형 내부의 온도 분포를 관찰할 수 있었다. 열전달에서 Analytical-Method 방법을 직접 손으로 풀던 문제를 프로그램을 이용하여 쉽게 값을 얻을 수 있었다.
늦게 제출하여서 죄송합니다. 보기에는 미흡하시지만 혼자서 Tecplot Program을 하면서 많을 것을 배우는 계기가 되었습니다.































소개글