가우스 구적법 (Gauss Quadrature)

소개글

가우스 구적법 (Gauss Quadrature)에 대한 보고서 자료입니다.

목차

Gauss Quadrature


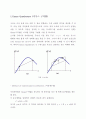
1. Gauss Quadrature (가우스 구적법)
2. 이론해 계산
3. 프로그램 알고리즘
4. 프로그램 리스트
5. 수치 적분 결과
6. 이론 해와 결과 비교 및 분석 고찰

본문내용

=2,3,4,5,6)
step 4 포인트에 맞는 weighting factor와 function arguments 를 찾는다.
step 5 이렇게 나온 x값을 원식 ()
에 넣는다.
step 6 을 구한다.
<플로우차트>
4. 프로그램 리스트
%n=2
clear all
format long
func=\'0.2+25*x-200*x^2+675*x^3-900*x^4+400*x^5\'
a=0; b=1;
xi1=0.577350269; xi2=-0.577350269;
c1=1.0; c2=1.0;
x1=(b+a)/2+(b-a)/2*xi1; x=x1; f1=eval(func);
x2=(b+a)/2+(b-a)/2*xi2; x=x2; f2=eval(func);
root=(b-a)/2*(c1*f1+c2*f2);
disp(sprintf(\'when n=2, 0 %n=3
clear all
format long
func=\'0.2+25*x-200*x^2+675*x^3-900*x^4+400*x^5\'
a=0; b=1;
xi1=0; xi2=0.774596669; xi3=-0.774596669;
c1=0.8888889; c2=0.5555556; c3=0.5555556;
x1=(b+a)/2+(b-a)/2*xi1; x=x1; f1=eval(func);
x2=(b+a)/2+(b-a)/2*xi2; x=x2; f2=eval(func);
x3=(b+a)/2+(b-a)/2*xi3; x=x3; f3=eval(func);
root=(b-a)/2*(c1*f1+c2*f2+c3*f3);
disp(sprintf(\'when n=3, 0 %n=5
clear all
format long
func=\'0.2+25*x-200*x^2+675*x^3-900*x^4+400*x^5\'
a=0; b=1;
xi1=-0.906179846; xi2=-0.538469310; xi3=0; xi4=0.538469310; xi5=0.906179846;
c1=0.2369269; c2=0.4786287; c3=0.5688889; c4=0.4786287; c5=0.2369269;
x1=(b+a)/2+(b-a)/2*xi1; x=x1; f1=eval(func);
x2=(b+a)/2+(b-a)/2*xi2; x=x2; f2=eval(func);
x3=(b+a)/2+(b-a)/2*xi3; x=x3; f3=eval(func);
x4=(b+a)/2+(b-a)/2*xi4; x=x4; f4=eval(func);
x5=(b+a)/2+(b-a)/2*xi5; x=x5; f5=eval(func);
root=(b-a)/2*(c1*f1+c2*f2+c3*f3+c4*f4+c5*f5);
disp(sprintf(\'when n=5, 0 %n=6
clear all
format long
func=\'0.2+25*x-200*x^2+675*x^3-900*x^4+400*x^5\'
a=0; b=1;
xi1=-0.932469514; xi2=-0.661209386; xi3=-0.238619186; xi4=0.238619186; xi5=0.661209386; xi6=0.932469514;
c1=0.1713245; c2=0.3607616; c3=0.4679139; c4=0.4679139; c5=0.3607616; c6=0.1713245;
x1=(b+a)/2+(b-a)/2*xi1; x=x1; f1=eval(func);
x2=(b+a)/2+(b-a)/2*xi2; x=x2; f2=eval(func);
x3=(b+a)/2+(b-a)/2*xi3; x=x3; f3=eval(func);
x4=(b+a)/2+(b-a)/2*xi4; x=x4; f4=eval(func);
x5=(b+a)/2+(b-a)/2*xi5; x=x5; f5=eval(func);
x6=(b+a)/2+(b-a)/2*xi6; x=x6; f6=eval(func);
root=(b-a)/2*(c1*f1+c2*f2+c3*f3+c4*f4+c5*f5+c6*f6);
disp(sprintf(\'when n=6, 0 5. 수치 적분 결과
n = 2
0.894444445584839
n = 3
1.450000016639698
n = 5
1.450000049832863
n = 6
1.449999914305718
<표 1 수치적분결과>
<그림 2 수치적분결과>
6. 이론 해와 결과 비교 및 분석 고찰
-이론 해와 결과 비교
이론해
수치해석값
1.45
n = 2
0.894444445584839
n = 3
1.450000016639698
n = 5
1.450000049832863
n = 6
1.449999914305718
<표 2 이론 해와 수치해석값>
이론 해와의 오차
오차값(절대값)
n=2일 때 이론 해와의 오차
0.55555555441516
n=3일 때 이론 해와의 오차
1.663969806386945e-008
n=5일 때 이론 해와의 오차
4.983286294724110e-008
n=6일 때 이론 해와의 오차
8.569428189275641e-008
<표 2 이론해와 수치해석값의 비교>
-분석 및 고찰
수치 해석 값과 이론 값 사이에는 엄연한 오차가 발생 하였다.
오차는 생각보다 컸으며 n=2일 때는 그 오차 값이 매우 커 수식을 잘못 사용하였는지 재검토 할 정도였다. 또 n=3 일 때 보다 n=5 , n=6 일 때 오차 값이 더 커 의아한 점이 있었다. 이를 분석 하여보니 0 <그림 3 (0
또 초반에 언급했듯이 n값이 커지면 오히려 round off error 발생률이 커진다. 따라서 작은 오차들이 모였기 때문에 n=3 일 때 보다 너 오차 값이 커졌을 것이다. 범위 내에 음수로 나오는 범위와 양수범위간의 차에서 유효 숫자로 인한 오차가 발생할 가능성이 매우 높다.

키워드

가우스 구적법,   프로그램 알고리즘,   Gauss,   알고리즘,   이론해 계산,   Gauss Quadrature,   가우스,   수치 적분 결과