목차
Ⅰ. Data의 대표값과 산포도
1) 산술평균
2) 표준편차와 표준오차
3) 변이계수
Ⅱ. 통계적 가설의 검정
1) 귀무가설과 대립가설
2) 가설검정 절차
3) 가설검정 결과 해석
Ⅲ. 분산분석표의 이해
1) 선형모형식
2) 분산분석표 작성
3) 분산분석 결과 해석
Ⅳ. 학습과제
Ⅴ. 학습과제 설명
Ⅵ. 참고문헌
1) 산술평균
2) 표준편차와 표준오차
3) 변이계수
Ⅱ. 통계적 가설의 검정
1) 귀무가설과 대립가설
2) 가설검정 절차
3) 가설검정 결과 해석
Ⅲ. 분산분석표의 이해
1) 선형모형식
2) 분산분석표 작성
3) 분산분석 결과 해석
Ⅳ. 학습과제
Ⅴ. 학습과제 설명
Ⅵ. 참고문헌
본문내용
, 165,
152, 144, 149, 157, 135, 142, 150, 132, 138, 164,
146, 158, 168, 126, 146, 142, 150, 156, 147, 173,
145, 138, 161, 128, 176, 145, 140, 135, 140, 147
아래 정답 설명 참고
3. 다음 각 항의 평균, 중앙값, 최빈값, 표준편차, 표준오차, 변이계수를 구하라.
(1) 7, 4, 10, 9, 15, 12, 9, 7
(2) 8, 11, 4, 3, 2, 5, 10, 6, 4, 1, 10, 8, 12, 6, 5, 7
(1) 평균 9.125 중앙값 9 최빈값 7, 9 표준편차 3.357 표준오차 1.187 변이계수 0.368
(2) 평균 6.375 중앙값 6 최빈값 4, 5, 6, 8, 10 표준편차 3.263 표준오차 0.816 변이계수 0.512
4. 벼 300개체에 대한 간장(稈長)을 측정하였더니, 평균 64 cm, 표준편차 4 cm였다.
(1) 60 cm와 68 cm 사이에 있는 개체수는 얼마인가? 204.78개
(2) 56 cm와 72 cm 사이에 있는 개체수는 얼마인가? 286.32개
(3) 75 cm 이상인 개체수는 얼마인가? 0.9개
(4) 55 cm 이하인 개체수는 얼마인가? 0.9개
Ⅴ. 학습과제 설명
학습과제 2
오름차순 정렬
[119, 125, 126, 128, 132, 135, 135, 135, 136, 138, 138, 140, 140, 142, 142, 144, 144, 145, 145, 146, 146, 147, 147, 148, 149, 150, 150, 152, 153, 154, 156, 157, 158, 161, 163, 164, 165, 168, 173, 176]
관찰값의 개수 40
계급수 5
계급폭은 (최댓값-최솟값)/5(=11.4)로 계산하여 사용했다.
계급 119~130.4, 130.4~141.8, 141.8~153.2, 153.2~164.6, 164.6~176
각 계급의 도수 4, 9, 16, 7, 4
계급값 = (하한값+상한값)/2
번호
계급
계급값()
도수()
누적도수
상대도수
누적상대도수
1
119~130.4
124.7
4
4
0.1(=4/40)
0.1
2
130.4~141.8
136.1
9
13
0.225(=9/40)
0.325
3
141.8~153.2
147.5
16
29
0.4(=16/40)
0.725
4
153.2~164.6
158.9
7
36
0.175(=7/40)
0.9
5
164.6~176
170.3
4
40
0.1(=4/40)
1
관찰값의 개수 40
계급수 10
계급폭은 (최댓값-최솟값)/10(=5.7)로 계산하여 사용했다.
계급 119~124.7, 124.7~130.4, 130.4~136.1, 136.1~141.8, 141.8~147.5,
147.5~153.2, 153.2~158.9, 158.9~164.6, 164.6~170.3, 170.3~176
각 계급의 도수 1, 3, 5, 4, 10, 6, 4, 3, 2, 2
번호
계급
계급값()
도수()
누적도수
상대도수
누적상대도수
1
119~124.7
121.85
1
1
0.025
0.025
2
124.7~130.4
127.55
3
4
0.075
0.1
3
130.4~136.1
133.25
5
9
0.125
0.225
4
136.1~141.8
138.95
4
13
0.1
0.325
5
141.8~147.5
144.65
10
23
0.25
0.575
6
147.5~153.2
150.35
6
29
0.15
0.725
7
153.2~158.9
156.05
4
33
0.1
0.825
8
158.9~164.6
161.75
3
36
0.075
0.9
9
164.6~170.3
167.45
2
38
0.05
0.95
10
170.3~176
173.15
2
40
0.05
1
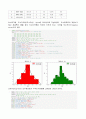
히스토그램, 도수다각형(도수곡선), Ogive은 파이썬으로 작성하였다. 도수분포표의 계급수가 많고 계급폭이 좁을 경우 도수다각형은 곡선에 가까게 되고, 이것을 도수곡선(frequency curve)라고 한다.
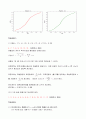
오자이브(ogive)는 도수분포표의 누적도수분포를 그래프로 나타낸 것이다.
학습과제 3
(1) 평균 = (7 + 4 + 10 + 9 + 15 + 12 + 9 + 7)/8 = 9.125
4, 7, 7, 9, 9, 10, 12, 15 (오름차순 정렬)
관찰값의 개수가 짝수이므로 중앙값은 다음과 같다.
관찰값 7과 9의 빈도수가 각각 2로 가장 크므로 최빈값은 7, 9이다.
표준편차는 편차(관찰값-평균)의 제곱합의 평균이고, 이때 표본의 개수가 n이면 n-1로 나누어 모수가 편의되지 않도록 계산한다.
표준오차는 표본평균의 표준편차로 이다. 모표준편차 를 모를 경우에는 표본표준편차 s를 사용하여 로 계산한다. 따라서 이 된다.
변이계수는 표본표준편차를 표본평균으로 나누어 계산한다.
변이계수 = 3.357/9.125 = 0.368
(2) (1)과 같은 방법으로 계산하면 된다.
1, 2, 3, 4, 4, 5, 5, 6, 6, 7, 8, 8, 10, 10, 11, 12 (오름차순 정렬)
학습과제 4
(1) 정규분포에서 확률변수가 에 존재할 확률은 68.26%이므로,
(이 구간에 있는 개체수) = 0.6826 X 300 = 204.97이다.
(2) 정규분포에서 확률변수가 에 존재할 확률은 95.44%이므로,
(이 구간에 있는 개체수) = 0.9544 X 300 = 286.32이다.
(3) 75를 정규화 하면 Z = (75-64)/4 = 2.75이다.
표준정규분포표에서 Z = 2.75에 해당하는 확률은 0.4970이다.
따라서 (75 cm 이상인 개체수) = (0.5-0.4970) X 300 = 0.9이다.
(4) 55를 정규화 하면 Z = (55-64)/4 = -2.75이다.
정규분포는 평균을 중심으로 대칭형이므로 Z = -2.75에 해당하는 확률은 0.4970이다.
따라서 (55 cm 이하인 개체수) = (0.5-0.4970) X 300 = 0.9이다.
Ⅵ. 참고문헌
박순직·한원식·정남진, 생물통계학, 한국방송대학교출판문화원, 2022.
과제 스트레스 싹~ 학점 쑥!
감사합니다.
152, 144, 149, 157, 135, 142, 150, 132, 138, 164,
146, 158, 168, 126, 146, 142, 150, 156, 147, 173,
145, 138, 161, 128, 176, 145, 140, 135, 140, 147
아래 정답 설명 참고
3. 다음 각 항의 평균, 중앙값, 최빈값, 표준편차, 표준오차, 변이계수를 구하라.
(1) 7, 4, 10, 9, 15, 12, 9, 7
(2) 8, 11, 4, 3, 2, 5, 10, 6, 4, 1, 10, 8, 12, 6, 5, 7
(1) 평균 9.125 중앙값 9 최빈값 7, 9 표준편차 3.357 표준오차 1.187 변이계수 0.368
(2) 평균 6.375 중앙값 6 최빈값 4, 5, 6, 8, 10 표준편차 3.263 표준오차 0.816 변이계수 0.512
4. 벼 300개체에 대한 간장(稈長)을 측정하였더니, 평균 64 cm, 표준편차 4 cm였다.
(1) 60 cm와 68 cm 사이에 있는 개체수는 얼마인가? 204.78개
(2) 56 cm와 72 cm 사이에 있는 개체수는 얼마인가? 286.32개
(3) 75 cm 이상인 개체수는 얼마인가? 0.9개
(4) 55 cm 이하인 개체수는 얼마인가? 0.9개
Ⅴ. 학습과제 설명
학습과제 2
오름차순 정렬
[119, 125, 126, 128, 132, 135, 135, 135, 136, 138, 138, 140, 140, 142, 142, 144, 144, 145, 145, 146, 146, 147, 147, 148, 149, 150, 150, 152, 153, 154, 156, 157, 158, 161, 163, 164, 165, 168, 173, 176]
관찰값의 개수 40
계급수 5
계급폭은 (최댓값-최솟값)/5(=11.4)로 계산하여 사용했다.
계급 119~130.4, 130.4~141.8, 141.8~153.2, 153.2~164.6, 164.6~176
각 계급의 도수 4, 9, 16, 7, 4
계급값 = (하한값+상한값)/2
번호
계급
계급값()
도수()
누적도수
상대도수
누적상대도수
1
119~130.4
124.7
4
4
0.1(=4/40)
0.1
2
130.4~141.8
136.1
9
13
0.225(=9/40)
0.325
3
141.8~153.2
147.5
16
29
0.4(=16/40)
0.725
4
153.2~164.6
158.9
7
36
0.175(=7/40)
0.9
5
164.6~176
170.3
4
40
0.1(=4/40)
1
관찰값의 개수 40
계급수 10
계급폭은 (최댓값-최솟값)/10(=5.7)로 계산하여 사용했다.
계급 119~124.7, 124.7~130.4, 130.4~136.1, 136.1~141.8, 141.8~147.5,
147.5~153.2, 153.2~158.9, 158.9~164.6, 164.6~170.3, 170.3~176
각 계급의 도수 1, 3, 5, 4, 10, 6, 4, 3, 2, 2
번호
계급
계급값()
도수()
누적도수
상대도수
누적상대도수
1
119~124.7
121.85
1
1
0.025
0.025
2
124.7~130.4
127.55
3
4
0.075
0.1
3
130.4~136.1
133.25
5
9
0.125
0.225
4
136.1~141.8
138.95
4
13
0.1
0.325
5
141.8~147.5
144.65
10
23
0.25
0.575
6
147.5~153.2
150.35
6
29
0.15
0.725
7
153.2~158.9
156.05
4
33
0.1
0.825
8
158.9~164.6
161.75
3
36
0.075
0.9
9
164.6~170.3
167.45
2
38
0.05
0.95
10
170.3~176
173.15
2
40
0.05
1
히스토그램, 도수다각형(도수곡선), Ogive은 파이썬으로 작성하였다. 도수분포표의 계급수가 많고 계급폭이 좁을 경우 도수다각형은 곡선에 가까게 되고, 이것을 도수곡선(frequency curve)라고 한다.
오자이브(ogive)는 도수분포표의 누적도수분포를 그래프로 나타낸 것이다.
학습과제 3
(1) 평균 = (7 + 4 + 10 + 9 + 15 + 12 + 9 + 7)/8 = 9.125
4, 7, 7, 9, 9, 10, 12, 15 (오름차순 정렬)
관찰값의 개수가 짝수이므로 중앙값은 다음과 같다.
관찰값 7과 9의 빈도수가 각각 2로 가장 크므로 최빈값은 7, 9이다.
표준편차는 편차(관찰값-평균)의 제곱합의 평균이고, 이때 표본의 개수가 n이면 n-1로 나누어 모수가 편의되지 않도록 계산한다.
표준오차는 표본평균의 표준편차로 이다. 모표준편차 를 모를 경우에는 표본표준편차 s를 사용하여 로 계산한다. 따라서 이 된다.
변이계수는 표본표준편차를 표본평균으로 나누어 계산한다.
변이계수 = 3.357/9.125 = 0.368
(2) (1)과 같은 방법으로 계산하면 된다.
1, 2, 3, 4, 4, 5, 5, 6, 6, 7, 8, 8, 10, 10, 11, 12 (오름차순 정렬)
학습과제 4
(1) 정규분포에서 확률변수가 에 존재할 확률은 68.26%이므로,
(이 구간에 있는 개체수) = 0.6826 X 300 = 204.97이다.
(2) 정규분포에서 확률변수가 에 존재할 확률은 95.44%이므로,
(이 구간에 있는 개체수) = 0.9544 X 300 = 286.32이다.
(3) 75를 정규화 하면 Z = (75-64)/4 = 2.75이다.
표준정규분포표에서 Z = 2.75에 해당하는 확률은 0.4970이다.
따라서 (75 cm 이상인 개체수) = (0.5-0.4970) X 300 = 0.9이다.
(4) 55를 정규화 하면 Z = (55-64)/4 = -2.75이다.
정규분포는 평균을 중심으로 대칭형이므로 Z = -2.75에 해당하는 확률은 0.4970이다.
따라서 (55 cm 이하인 개체수) = (0.5-0.4970) X 300 = 0.9이다.
Ⅵ. 참고문헌
박순직·한원식·정남진, 생물통계학, 한국방송대학교출판문화원, 2022.
과제 스트레스 싹~ 학점 쑥!
감사합니다.
추천자료
 사료학(농후사료, 조사료, 사료첨가제, 사료사양표준, 사료계산법, 사료배합, 사료배합작성방법)
사료학(농후사료, 조사료, 사료첨가제, 사료사양표준, 사료계산법, 사료배합, 사료배합작성방법) (2022년 방송통신대 Visual C++프로그래밍 출석수업대체과제물)교재 1 장의 1.5절 버튼 사용...
(2022년 방송통신대 Visual C++프로그래밍 출석수업대체과제물)교재 1 장의 1.5절 버튼 사용... 2022년 2학기 생물통계학 출석수업대체시험 과제물(주관식 문제)
2022년 2학기 생물통계학 출석수업대체시험 과제물(주관식 문제) 2023년 2학기 방송통신대 생물통계학 출석수업대체과제물)아래 첨부한 파일(생물통계학 출석...
2023년 2학기 방송통신대 생물통계학 출석수업대체과제물)아래 첨부한 파일(생물통계학 출석... 2023년 2학기 생물통계학 출석수업대체시험 과제물(주관식 문제)
2023년 2학기 생물통계학 출석수업대체시험 과제물(주관식 문제) 보건통계학 2024년 2학기 방송통신대 출석수업과제물) 다음 문제들에 대해 풀이 과정을 제시...
보건통계학 2024년 2학기 방송통신대 출석수업과제물) 다음 문제들에 대해 풀이 과정을 제시... 2024년 2학기 생물통계학 출석수업대체시험 과제물(주관식 문제)
2024년 2학기 생물통계학 출석수업대체시험 과제물(주관식 문제)





























소개글