목차
Ⅰ. 실험 요약 5-8
1.1 실험 목적 5
1.2 이론적 배경 5-7
1.3 실험 장비 7
1.4 실험 방법 8
Ⅱ. 시험 결과 및 비교 그래프 9-15
2.1 자중에 의한 처짐 9
2.2 이론값 계산 10-12
1). 집중하중 10
2). 모멘트 11
3). 복합하중 12
2.3 이론값 실험값 비교 표 12-13
1). 집중하중 12
2). 모멘트 13
3). 복합하중 13
2.4 이론값 실험값 그래프 14-17
1). 집중하중 14
2). 모멘트 15
3). 복합하중 16-17
Ⅲ. 고찰 18
Ⅳ. 참고문헌 19
1.1 실험 목적 5
1.2 이론적 배경 5-7
1.3 실험 장비 7
1.4 실험 방법 8
Ⅱ. 시험 결과 및 비교 그래프 9-15
2.1 자중에 의한 처짐 9
2.2 이론값 계산 10-12
1). 집중하중 10
2). 모멘트 11
3). 복합하중 12
2.3 이론값 실험값 비교 표 12-13
1). 집중하중 12
2). 모멘트 13
3). 복합하중 13
2.4 이론값 실험값 그래프 14-17
1). 집중하중 14
2). 모멘트 15
3). 복합하중 16-17
Ⅲ. 고찰 18
Ⅳ. 참고문헌 19
본문내용
달아 집중하중을 가한다.
각각 게이지의 값을 측정한다.
추를 바꿔 위 과정을 반복한다.
2) 모멘트
양단 지지보를 고정한다.
게이지의 영점을 조정한다.
보의 왼쪽으로부터 지점에 디스크를 설치한 후 양쪽에 추를 단다.
각각 게이지의 값을 측정한다.
추를 바꿔 위 과정을 반복한다.
3) 복합 하중
양단 지지보를 고정한다.
게이지의 영점을 조정한다.
보의 오른쪽으로부터 지점에 추를 달아 집중하중을 가한다.
보의 왼쪽으로부터 지점에 디스크를 설치한 후 양쪽에 추를 단다.
각각 게이지의 값을 측정한다.
추를 바꿔 위 과정을 반복한다.
2. 실험 결과 및 비교 그래프
2.1 자중에 의한 처짐
실험에서 고려해야하는 사항이 있다. 시험을 진행할 때 보의 자중이 걸려있는 상태에 서 게이지의 영점을 맞췄다. 따라서 정확한 값을 알기 위해서는 게이지 측정값과 이론값에 자중에 의한 처짐을 더해야 한다. 자중에 의한 하중 조건, 게이지 위치에서 보의 처짐은 다음과 같다.
[. 보의 자중에 의한 처짐]
2.2 이론값 계산 [2]
이론값 계산은 특이함수법을 사용해서 계산한다.
1). 집중하중
[. 집중하중 FBD]
이다.
경계조건에 따라 이다. 따라서
경계조건에 따라 이다. 따라서
경계조건에 따라 , 이므로
이다 따라서
,
이다.
2). 모멘트
[. 모멘트 FBD]
이다.
경계조건에 따라 이다. 따라서
경계조건에 따라 이다. 따라서
경계조건에 따라 , 이므로
이다 따라서
,
이다
3). 복합하중
[. 복합하중 FBD]
복합 하중은 중첩의 원리에 따라 (식1)과 (식2)를 더해 구할 수 있다. 결과는 다음과 같다.
2.3 이론값 실험값 비교 및 그래프
1) 집중하중
(단위: mm)
Gauge
실험값
이론값
오차율(%)
5N
1
-1.969
-1.918
2.659
2
-3.845
-3.710
3.638
3
-2.315
-2.174
6.485
10N
1
-2.520
-2.436
3.448
2
-5.122
-4.930
3.894
3
-3.279
-3.028
8.289
.
2) 모멘트
(단위: mm)
Gauge
실험값
이론값
오차율(%)
5N
1
-1.443
-1.447
0.2557
2
-2.671
-2.673
0.074
3
-1.420
-1.412
0.602
10N
1
-1.476
-1.493
1.165
2
-2.826
-2.856
1.050
3
-1.510
-1.503
0.465
.
3) 복합하중
(단위: mm)
Gauge
실험값
이론값
오차율(%)
P : 5N
M : 5N
1
-1.949
-1.968
0.965
2
-3.916
-3.893
0.590
3
-2.357
-2.266
4.015
P : 5N
M : 10N
1
-1.992
-2.011
0.944
2
-4.081
-4.076
0.122
3
-2.457
-2.357
4.242
P : 10N
M : 5N
1
-2.519
-2.485
1.368
2
-5.227
-5.113
2.229
3
-3.338
-3.119
7.021
P : 10N
M : 10N
1
-2.545
-2.530
0.592
2
-5.364
-5.296
1.283
3
-3.413
-3.211
6.290
.
2.4 이론값 실험값 그래프
순수 집중하중, 모멘트, 복합하중에 의한 처짐만을 비교하기 위해 자중에 의한 처짐은 제고하고 그래프를 그려 비교한다.
1). 집중하중
. _집중하중 5N
. _집중하중 10N
2). 모멘트
. _모멘트 5N
. _모멘트 10N
3). 복합하중
. _집중하중 5N, 모멘트 5N
. _집중하중 10N, 모멘트 5N
. _집중하중 5N, 모멘트 10N
. _모멘트 10N, 모멘트 10N
3. 고찰
이번 실험을 통해 보에 하중에 따른 처짐량 를 측정하고 계산한 이론값과 비교하는 실험을 진행했다. 각 실험에서 gage3의 오차율이 가장 크게 나타났다. 따라서 gage3 장비의 오차율이 있음을 알 수 있다. 이론값을 계산할 때 특이함수법을 사용하여 계산했다. 따라서 특이함수의 사용 방법에 대해 이해할 수 있었다, 여러하중 조건에서 보의 처짐을과 재료의 거동을 이해할 수 있었다.
-각 실험의 처짐량 비교
보의 자중에 의한 처짐을 빼고 각 실험에서의 처짐량을 비교한다. 집중하중의 처짐과 모멘트에 의한 처짐을 합치면 복합 하중의 처짐과 비슷한 값을 가진다. 따라서 이론에서 알아봤던 중첩의 원리가 성립함을 알 수 있다. 또한 집중하중에 의한 하중중이 모멘트에 의한 하중보다 큰 값을 가짐을 알 수 있다.
-실험값과 이론값 비교
이론값과 실험값의 오차율은 7%를 넘지 않는다. 따라서 실험이 잘 진행됐음을 알 수 있다. 실험값과 이론값을 비교했을 때 대부분 실험값이 큰 것을 볼 수 있다. 이 이유를 생각하면 이론에서는 2차원 평면에서 해석했을 때 값을 계산했다. 하지만 실험에서는 3차원으로 변형이 발생한다. 따라서 실험값과 이론값의 차이는 여기서 발생했음을 예상할 수 있다.
-오차의 원인 분석
오차의 원인을 분석하면 다음과 같다.
첫 번째 시편의 부식이다. 사진과 같이 시편을 관찰하면 표면에 녹이 있는 것을 관찰할 수 있다. 이는 시편의 물성치와 표면에 영향을 주어 응력집중을 일으켜 오차의 원인이 된다.
두 번째 변형량 계산 방법이다. 이론값을 계산할 때 계산을 간편하게 하기 위해 2차원으로 가정하고 문제를 푼다. 하지만 실험에서는 3차원에서 변형이 발생하기 때문에 원래의 변형 값보다 더 큰 값을 가진다.
마지막은 추를 올릴 때 발생하는 충격이다. 추를 장치에 올릴 때 충격량이 발생하고 이는 변형량에 영향을 끼치는 원인이 된다.
4. 참고문헌
[1]: 송동근, 보의 처짐 교안
[2]: SI재료역학 9th edition, Barry J. Goodno & James M. Gere, CENGAGE, p776~790
[3]: SI재료역학 9th edition, Barry J. Goodno & James M. Gere, CENGAGE, p795~798
[4]:심재헌. 특이함수에 의한 보의 처짐 및 부정정 보 문제의 풀이. 대한기계학회지, 1983, 23.6: 448-458.
[Fig 1, 2, 3]: 보의 처짐 교안
각각 게이지의 값을 측정한다.
추를 바꿔 위 과정을 반복한다.
2) 모멘트
양단 지지보를 고정한다.
게이지의 영점을 조정한다.
보의 왼쪽으로부터 지점에 디스크를 설치한 후 양쪽에 추를 단다.
각각 게이지의 값을 측정한다.
추를 바꿔 위 과정을 반복한다.
3) 복합 하중
양단 지지보를 고정한다.
게이지의 영점을 조정한다.
보의 오른쪽으로부터 지점에 추를 달아 집중하중을 가한다.
보의 왼쪽으로부터 지점에 디스크를 설치한 후 양쪽에 추를 단다.
각각 게이지의 값을 측정한다.
추를 바꿔 위 과정을 반복한다.
2. 실험 결과 및 비교 그래프
2.1 자중에 의한 처짐
실험에서 고려해야하는 사항이 있다. 시험을 진행할 때 보의 자중이 걸려있는 상태에 서 게이지의 영점을 맞췄다. 따라서 정확한 값을 알기 위해서는 게이지 측정값과 이론값에 자중에 의한 처짐을 더해야 한다. 자중에 의한 하중 조건, 게이지 위치에서 보의 처짐은 다음과 같다.
[. 보의 자중에 의한 처짐]
2.2 이론값 계산 [2]
이론값 계산은 특이함수법을 사용해서 계산한다.
1). 집중하중
[. 집중하중 FBD]
이다.
경계조건에 따라 이다. 따라서
경계조건에 따라 이다. 따라서
경계조건에 따라 , 이므로
이다 따라서
,
이다.
2). 모멘트
[. 모멘트 FBD]
이다.
경계조건에 따라 이다. 따라서
경계조건에 따라 이다. 따라서
경계조건에 따라 , 이므로
이다 따라서
,
이다
3). 복합하중
[. 복합하중 FBD]
복합 하중은 중첩의 원리에 따라 (식1)과 (식2)를 더해 구할 수 있다. 결과는 다음과 같다.
2.3 이론값 실험값 비교 및 그래프
1) 집중하중
(단위: mm)
Gauge
실험값
이론값
오차율(%)
5N
1
-1.969
-1.918
2.659
2
-3.845
-3.710
3.638
3
-2.315
-2.174
6.485
10N
1
-2.520
-2.436
3.448
2
-5.122
-4.930
3.894
3
-3.279
-3.028
8.289
.
2) 모멘트
(단위: mm)
Gauge
실험값
이론값
오차율(%)
5N
1
-1.443
-1.447
0.2557
2
-2.671
-2.673
0.074
3
-1.420
-1.412
0.602
10N
1
-1.476
-1.493
1.165
2
-2.826
-2.856
1.050
3
-1.510
-1.503
0.465
.
3) 복합하중
(단위: mm)
Gauge
실험값
이론값
오차율(%)
P : 5N
M : 5N
1
-1.949
-1.968
0.965
2
-3.916
-3.893
0.590
3
-2.357
-2.266
4.015
P : 5N
M : 10N
1
-1.992
-2.011
0.944
2
-4.081
-4.076
0.122
3
-2.457
-2.357
4.242
P : 10N
M : 5N
1
-2.519
-2.485
1.368
2
-5.227
-5.113
2.229
3
-3.338
-3.119
7.021
P : 10N
M : 10N
1
-2.545
-2.530
0.592
2
-5.364
-5.296
1.283
3
-3.413
-3.211
6.290
.
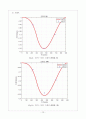
2.4 이론값 실험값 그래프
순수 집중하중, 모멘트, 복합하중에 의한 처짐만을 비교하기 위해 자중에 의한 처짐은 제고하고 그래프를 그려 비교한다.
1). 집중하중
. _집중하중 5N
. _집중하중 10N
2). 모멘트
. _모멘트 5N
. _모멘트 10N
3). 복합하중
. _집중하중 5N, 모멘트 5N
. _집중하중 10N, 모멘트 5N
. _집중하중 5N, 모멘트 10N
. _모멘트 10N, 모멘트 10N
3. 고찰
이번 실험을 통해 보에 하중에 따른 처짐량 를 측정하고 계산한 이론값과 비교하는 실험을 진행했다. 각 실험에서 gage3의 오차율이 가장 크게 나타났다. 따라서 gage3 장비의 오차율이 있음을 알 수 있다. 이론값을 계산할 때 특이함수법을 사용하여 계산했다. 따라서 특이함수의 사용 방법에 대해 이해할 수 있었다, 여러하중 조건에서 보의 처짐을과 재료의 거동을 이해할 수 있었다.
-각 실험의 처짐량 비교
보의 자중에 의한 처짐을 빼고 각 실험에서의 처짐량을 비교한다. 집중하중의 처짐과 모멘트에 의한 처짐을 합치면 복합 하중의 처짐과 비슷한 값을 가진다. 따라서 이론에서 알아봤던 중첩의 원리가 성립함을 알 수 있다. 또한 집중하중에 의한 하중중이 모멘트에 의한 하중보다 큰 값을 가짐을 알 수 있다.
-실험값과 이론값 비교
이론값과 실험값의 오차율은 7%를 넘지 않는다. 따라서 실험이 잘 진행됐음을 알 수 있다. 실험값과 이론값을 비교했을 때 대부분 실험값이 큰 것을 볼 수 있다. 이 이유를 생각하면 이론에서는 2차원 평면에서 해석했을 때 값을 계산했다. 하지만 실험에서는 3차원으로 변형이 발생한다. 따라서 실험값과 이론값의 차이는 여기서 발생했음을 예상할 수 있다.
-오차의 원인 분석
오차의 원인을 분석하면 다음과 같다.
첫 번째 시편의 부식이다. 사진과 같이 시편을 관찰하면 표면에 녹이 있는 것을 관찰할 수 있다. 이는 시편의 물성치와 표면에 영향을 주어 응력집중을 일으켜 오차의 원인이 된다.
두 번째 변형량 계산 방법이다. 이론값을 계산할 때 계산을 간편하게 하기 위해 2차원으로 가정하고 문제를 푼다. 하지만 실험에서는 3차원에서 변형이 발생하기 때문에 원래의 변형 값보다 더 큰 값을 가진다.
마지막은 추를 올릴 때 발생하는 충격이다. 추를 장치에 올릴 때 충격량이 발생하고 이는 변형량에 영향을 끼치는 원인이 된다.
4. 참고문헌
[1]: 송동근, 보의 처짐 교안
[2]: SI재료역학 9th edition, Barry J. Goodno & James M. Gere, CENGAGE, p776~790
[3]: SI재료역학 9th edition, Barry J. Goodno & James M. Gere, CENGAGE, p795~798
[4]:심재헌. 특이함수에 의한 보의 처짐 및 부정정 보 문제의 풀이. 대한기계학회지, 1983, 23.6: 448-458.
[Fig 1, 2, 3]: 보의 처짐 교안






































소개글