목차
1. 정규분포의 개념
2. 정규분포 곡선
3. 정규분포의 특징
2. 정규분포 곡선
3. 정규분포의 특징
본문내용
집단에서 무작위로(Randomly) 하나의 개체를 뽑아 어떤 특성에 대해 측정하였다면,
이 개체의 측정값이 μ+3σ보다 크거나 μ-3σ보다 작을 가능성(확률)은
단지 0.27%에 불과하다. (0.27% = 100% - 99.73%)
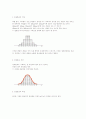
- 평균(u)에서 양쪽으로 1σ만큼의 면적 : 60.26%
- 평균(u)에서 양쪽으로 2σ만큼의 면적 : 95.44%
- 평균(u)에서 양쪽으로 3σ만큼의 면적 : 99.73%
4)파티에 참석한 성인 남성의 키 사례 :
모집단의 평균값(μ)은 170cm이고, 표준편차(σ)는 5cm라고 하자.
만약 그 집단에서 무작위로 한 사람을 선정했을 때,
그 사람의 키가 155cm(μ-3σ)보다 작거나
185cm(μ+3σ)보다 클 확률은 아주 작을 것이다. ( 0.27% )
이 개체의 측정값이 μ+3σ보다 크거나 μ-3σ보다 작을 가능성(확률)은
단지 0.27%에 불과하다. (0.27% = 100% - 99.73%)
- 평균(u)에서 양쪽으로 1σ만큼의 면적 : 60.26%
- 평균(u)에서 양쪽으로 2σ만큼의 면적 : 95.44%
- 평균(u)에서 양쪽으로 3σ만큼의 면적 : 99.73%
4)파티에 참석한 성인 남성의 키 사례 :
모집단의 평균값(μ)은 170cm이고, 표준편차(σ)는 5cm라고 하자.
만약 그 집단에서 무작위로 한 사람을 선정했을 때,
그 사람의 키가 155cm(μ-3σ)보다 작거나
185cm(μ+3σ)보다 클 확률은 아주 작을 것이다. ( 0.27% )























소개글