
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
-
11
-
12
-
13
-
14
-
15
-
16
-
17
-
18
-
19
-
20
-
21
-
22
-
23
-
24
-
25
-
26
-
27
-
28
-
29
-
30
-
31
-
32
-
33
-
34
-
35
-
36
-
37
-
38
-
39
-
40
-
41
-
42
-
43
-
44
-
45
-
46
-
47
-
48
-
49
-
50
-
51
-
52
-
53
-
54
-
55
-
56
-
57
-
58
-
59
-
60
-
61
-
62
-
63
-
64
-
65


목차
문제 1) X1,X2,...,Xn ∼ N(200, 302)라 하자. 표본크기가 40인 표본을 5번 추출하여 평균과 분산 및 기타 정규분포에 관한 통계량들을 통해 정규분포를 이루는지를 알아보자.
문제 2) X11,..., X1n ∼ Exp(1) .....
X21,..., X2n ∼ Exp(2) .....
X31,..., X3n ∼ Exp(3)라 하자. 이때 표본의 크기가 30인 표본을 3번 추출하여 평균과 분산 및 기타 정규분포에 관한 통계량들을 통해 정규분포를 이루는 지 알아보자. 그리고 또한 OUTPUT에서 MEAN과 STDEV(S,E)를 주의깊게 살펴보자.
문제 3) X1,...,Xn,...∼Exp(5) 이라 하자. 이때 난수발생함수를 이용하여 가상적 분포의 Central Limit Theorem 실례를 보이고 N의 값이 증가하는 경우도 아울러 생각해보자.
문제 4) X1, X2 ∼ U(a, b)인 Random Variable이라 하자. 이 경우에서도 마찬가지로 표본의 크기가 커짐에 따라 CLT에 가까워짐을 시뮬레이트해보고, 모수의 값이 달라짐에 따라 또 어떻게 달라지는 가에 대해서도 주목해보자.
문제 5) X1, X2,..., Xn 이 베르누이확률변수라 하자. 이때 P값과 N값을 달리하면서 그 결과치를 비교해보면서 CLT가 됨을 증명해보아라. 여기서 중요한 것은 베르누이에 대한 난수발생함수가 없기 때문에 UNIFORM난수발생함수를 이용하여라. 단, 프로그램은 MACRO명령을 써서 프로그램밍하여라.
문제 2) X11,..., X1n ∼ Exp(1) .....
X21,..., X2n ∼ Exp(2) .....
X31,..., X3n ∼ Exp(3)라 하자. 이때 표본의 크기가 30인 표본을 3번 추출하여 평균과 분산 및 기타 정규분포에 관한 통계량들을 통해 정규분포를 이루는 지 알아보자. 그리고 또한 OUTPUT에서 MEAN과 STDEV(S,E)를 주의깊게 살펴보자.
문제 3) X1,...,Xn,...∼Exp(5) 이라 하자. 이때 난수발생함수를 이용하여 가상적 분포의 Central Limit Theorem 실례를 보이고 N의 값이 증가하는 경우도 아울러 생각해보자.
문제 4) X1, X2 ∼ U(a, b)인 Random Variable이라 하자. 이 경우에서도 마찬가지로 표본의 크기가 커짐에 따라 CLT에 가까워짐을 시뮬레이트해보고, 모수의 값이 달라짐에 따라 또 어떻게 달라지는 가에 대해서도 주목해보자.
문제 5) X1, X2,..., Xn 이 베르누이확률변수라 하자. 이때 P값과 N값을 달리하면서 그 결과치를 비교해보면서 CLT가 됨을 증명해보아라. 여기서 중요한 것은 베르누이에 대한 난수발생함수가 없기 때문에 UNIFORM난수발생함수를 이용하여라. 단, 프로그램은 MACRO명령을 써서 프로그램밍하여라.
본문내용
********+
| ******+++
| *******+++
0.5+*+++++
+----+----+----+----+----+----+----+----+----+----+
-2 -1 0 +1 +2
⑧ %CLTB1P(P=0.1, N=100, M=1000, SEED=91910141)
Empirical Distribution of sumy
sumy=sum of b(1, p)variables from each sample of size n
%cltb1p(p=0.1, n=100, m=1000, seed=91910141)
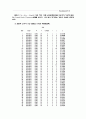
UNIVARIATE PROCEDURE
Variable=SUMY
Moments
N 1000 Sum Wgts 1000
Mean 9.967 Sum 9967
Std Dev 2.953072 Variance 8.720632
Skewness 0.182568 Kurtosis -0.19363
USS 108053 CSS 8711.911
CV 29.62849 Std Mean 0.093384
T:Mean=0 106.731 Prob>|T| 0.0
Sgn Rank 250250 Prob>|S| 0.0001
Num ^= 0 1000
W:Normal 0.969999 Prob
100% Max 19 99% 17
75% Q3 12 95% 15
50% Med 10 90% 14
25% Q1 8 10% 6
0% Min 3 5% 5
1% 4
Range 16
Q3-Q1 4
Mode 9
Extremes
Lowest Obs Highest Obs
3( 930) 18( 952)
3( 561) 19( 575)
3( 513) 19( 659)
3( 457) 19( 686)
3( 128) 19( 756)
-------------------------------------------------------------- Simulation#5 13
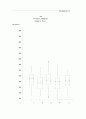
UNIVARIATE PROCEDURE
Variable=SUMY
Histogram # Boxplot
19.5+** 4 0
.* 3 |
.*** 8 |
.***** 14 |
.************** 41 |
.******************* 56 |
.************************** 76 |
.********************************* 97 +-----+
11.5+************************************** 113 | |
.****************************************** 126 *-----*
.*********************************************** 139 | + |
.**************************************** 120 +-----+
.******************************** 94 |
.*************** 45 |
.************ 35 |
.******** 22 |
3.5+*** 7 |
----+----+----+----+----+----+----+----+----+--
* may represent up to 3 counts
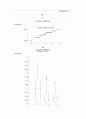
Normal Probability Plot
19.5+ *
| *
| ***+
| ****+
| *****+
| *****++
| ****++
| ****++
11.5+ ****+
| ****+
| *****+
| ****+
| *****+
| ****+
| *****+
| ******++
3.5+* +++
+----+----+----+----+----+----+----+----+----+----+
-2 -1 0 +1 +2
참고로 sas 프로그램을 출력해본다.
* sas macro program for clt applied on b(1, p) variables;
option ps=60 ls=78 nodate pageno=1;
%macro cltb1p(p= ,n= ,m= , seed= );
data b; p=&p; n=&n; m=&m; seed=&seed;
do i=1 to m;
do j=1 to n;
u=ranuni(seed); y=(u
* y is a b(1, p) variable;
output; end; end;
run;
-------------------------------------------------------------- Simulation#5 14
proc means data=b sum noprint;
by i;
var y;
output out=mout sum=sumy;
run;
title \'Empirical Distribution of sumy\';
title2 \'sumy=sum of b(1, p)variables from each sample of size n\';
title3 \'%cltb1p(p=0.1, n=100, m=1000, seed=91910141)\';
proc univariate data=mout plot normal;
var sumy;
run;
%mend;
%cltb1p(p=0.1, n=100, m=1000, seed=91910141)
우리가 예상했던 대로 N값이 커질수록 정규성이 가까워짐을 알 수 있다. 또한 대칭성이 인정되는 분포는 그 만큼 빠르게 정규분포로 근사함을 알 수 있다.
위 5문제를 통해 각각의 분포의 중심극한정리를 확인해보았다. 사실, 수학적인 개념을 정식적인 표본으로 실험하기란 불가능하므로 약간의 변칙적인 방법 컴퓨터시뮬레이션을 이용해보았다.
어떤 확률분포를 다른 분포로 근사화시키는 것이 매우 유용한 경우인 것은 우리가 잘 알고 있다. 원래의 분포함수를 수학적으로 조작하기 어렵거나 확률을 구할때 많은 계산량이 요구되는 경우가 이에 해당된다.
모집단의 확률분포가 이산형이든 연속형이든 한정된(Limited)분산만 가진다면 그 분포는 표본의 크기가 커질수록 정규분포에 가까워진다고 최종적인 결론을 내릴수가 있겠다. 다시 말하자면, 수학적인 증명으로 내려오던 CLT가 컴퓨터를 이용한 새로운 방법으로 증명된다고 할 수 있겠다.
| ******+++
| *******+++
0.5+*+++++
+----+----+----+----+----+----+----+----+----+----+
-2 -1 0 +1 +2
⑧ %CLTB1P(P=0.1, N=100, M=1000, SEED=91910141)
Empirical Distribution of sumy
sumy=sum of b(1, p)variables from each sample of size n
%cltb1p(p=0.1, n=100, m=1000, seed=91910141)
UNIVARIATE PROCEDURE
Variable=SUMY
Moments
N 1000 Sum Wgts 1000
Mean 9.967 Sum 9967
Std Dev 2.953072 Variance 8.720632
Skewness 0.182568 Kurtosis -0.19363
USS 108053 CSS 8711.911
CV 29.62849 Std Mean 0.093384
T:Mean=0 106.731 Prob>|T| 0.0
Sgn Rank 250250 Prob>|S| 0.0001
Num ^= 0 1000
W:Normal 0.969999 Prob
100% Max 19 99% 17
75% Q3 12 95% 15
50% Med 10 90% 14
25% Q1 8 10% 6
0% Min 3 5% 5
1% 4
Range 16
Q3-Q1 4
Mode 9
Extremes
Lowest Obs Highest Obs
3( 930) 18( 952)
3( 561) 19( 575)
3( 513) 19( 659)
3( 457) 19( 686)
3( 128) 19( 756)
-------------------------------------------------------------- Simulation#5 13
UNIVARIATE PROCEDURE
Variable=SUMY
Histogram # Boxplot
19.5+** 4 0
.* 3 |
.*** 8 |
.***** 14 |
.************** 41 |
.******************* 56 |
.************************** 76 |
.********************************* 97 +-----+
11.5+************************************** 113 | |
.****************************************** 126 *-----*
.*********************************************** 139 | + |
.**************************************** 120 +-----+
.******************************** 94 |
.*************** 45 |
.************ 35 |
.******** 22 |
3.5+*** 7 |
----+----+----+----+----+----+----+----+----+--
* may represent up to 3 counts
Normal Probability Plot
19.5+ *
| *
| ***+
| ****+
| *****+
| *****++
| ****++
| ****++
11.5+ ****+
| ****+
| *****+
| ****+
| *****+
| ****+
| *****+
| ******++
3.5+* +++
+----+----+----+----+----+----+----+----+----+----+
-2 -1 0 +1 +2
참고로 sas 프로그램을 출력해본다.
* sas macro program for clt applied on b(1, p) variables;
option ps=60 ls=78 nodate pageno=1;
%macro cltb1p(p= ,n= ,m= , seed= );
data b; p=&p; n=&n; m=&m; seed=&seed;
do i=1 to m;
do j=1 to n;
u=ranuni(seed); y=(u
* y is a b(1, p) variable;
output; end; end;
run;
-------------------------------------------------------------- Simulation#5 14
proc means data=b sum noprint;
by i;
var y;
output out=mout sum=sumy;
run;
title \'Empirical Distribution of sumy\';
title2 \'sumy=sum of b(1, p)variables from each sample of size n\';
title3 \'%cltb1p(p=0.1, n=100, m=1000, seed=91910141)\';
proc univariate data=mout plot normal;
var sumy;
run;
%mend;
%cltb1p(p=0.1, n=100, m=1000, seed=91910141)
우리가 예상했던 대로 N값이 커질수록 정규성이 가까워짐을 알 수 있다. 또한 대칭성이 인정되는 분포는 그 만큼 빠르게 정규분포로 근사함을 알 수 있다.
위 5문제를 통해 각각의 분포의 중심극한정리를 확인해보았다. 사실, 수학적인 개념을 정식적인 표본으로 실험하기란 불가능하므로 약간의 변칙적인 방법 컴퓨터시뮬레이션을 이용해보았다.
어떤 확률분포를 다른 분포로 근사화시키는 것이 매우 유용한 경우인 것은 우리가 잘 알고 있다. 원래의 분포함수를 수학적으로 조작하기 어렵거나 확률을 구할때 많은 계산량이 요구되는 경우가 이에 해당된다.
모집단의 확률분포가 이산형이든 연속형이든 한정된(Limited)분산만 가진다면 그 분포는 표본의 크기가 커질수록 정규분포에 가까워진다고 최종적인 결론을 내릴수가 있겠다. 다시 말하자면, 수학적인 증명으로 내려오던 CLT가 컴퓨터를 이용한 새로운 방법으로 증명된다고 할 수 있겠다.
















































































소개글