물리 실험 - 이중슬릿에 의한 빛의 간섭과 회절 - 예비보고서

소개글

물리 실험 - 이중슬릿에 의한 빛의 간섭과 회절 - 예비보고서에 대한 보고서 자료입니다.

목차

1. 실험 목적

2. 실험 원리

3. 실험 기구 및 장치

4. 실험 방법

본문내용

건에 따라 간섭무늬가 나타난다.
따라서 스크린상의 가장 밝은 부분(광축)과 m번째 밝은 무늬 간와의 거리을
라고 하면 각
가 작을
때는
이고
이므로
(12)
로 나타낼 수 있다. 그러므로
와
를 측정함으로써 슬릿간격
를 구할 수 있다.
3. 실험 기구 및 장치
레이저, 이중슬릿, 광학대
4. 실험 방법
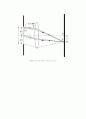
(1) 광학대 위에 레이저, 슬릿, 스크린을 장치한다. (그림 3)
(2) 슬릿과 스크린의 간격
를 적당히 정하고 그 값을 측정한다.
(3) 스크린상의 가장 밝은 간섭 무늬의 중심으로부터 m번째 밝은 무늬의 중심까지의 거리간격
를 측정한다.
이 때 m은 실험자가 임의 로 정한다.
(4)
를 변화시키면서 간섭무늬 간격을 측정 한다.
(5) (12)식으로부터 거리
를 계산하여 구한다.
(주의) 슬릿의 면에 지문이 찍히지 않도록 주의한다.
<참고자료>
회절
회절현상은 광원과 스크린 사이에 구멍이나 장애물이 있을 때 빛의 간섭현상에 의하여 발생한다. Freanel 회절은 광원과 스크린 사이의 거리가 유한할 경우에 발생하고 무한한 경우에는 Frauhofer 회절이라고 한다.
Fresnel 과 Fraunhofer 회절과 거리와의 관계.
Fraunhofer 회절에서는 평행한 광원이 구멍에 도달하고 평행한 광선이 구멍을 떠나간다.
(a) Fresnel 회절. 광원과 스크린 둘다 구멍과 가깝다. 광원으로부터 나온 빛과 스크린으로 가는 빛은 평행하지 않다.
(b) Fraunhofer 회절. 광원과 스크린 둘다 구멍에서 아주 먼 곳에 있다. 구멍에 입사해 들어가는 빛이나 구멍을 떠나서 스크린으로 가는 빛 둘 다 평행하다.(c) 광원과 스크린이 가까울 때 수렴렌즈를 두 개 사용하면 Fraunhofer 조건을 만족시킬 수 있다.">
크기가 a인 단일 슬릿을 y의 아주 작은 영역으로 나누면 각각의 영역은 Huygens의 2차 파의 파 원(波源)으로 생각할 수 있고 스쿠린 위의 점 P에 전기장 진폭 E 만큼의 기여를 하게 된다. 점 P에서의 총 전기장 E0
는 슬릿의 각 영역에서 나오는 전기장 기여의 합으로 나타 난다.
★Huygens의 원리 : 파면 위의 모든 점들은 제 2차파의 점광원으로 고려된다. 시간 t이후의 새로운 파면의 위치는 제 2차파들의 포락선(evnvelope)에 의하여 형성된다.
경로차/ = 위상차/ (2 ) 이므로
( y sin )/ = / (2 )
= (2 / ) y sin
파면을 폭이 좁은 많은 조각으로 나눈다.
(a) 각 전기장의 세기가 모두 같은 위상일 때의 페이서도( =0, =0),
(b) 각 전기장의 세기가 그 앞의 세기에 비하여 약간의 위상차가 있을 때의 페이서도,
(c) 슬릿을 무한히 많은 수로 나눈 극한에서의 페이서도.
단일 슬릿에 의한 Fraunhofer 회절에서 파의 간서에 의한 강도 변화를 살펴보자.
슬릿 중앙의 아주 작은 영역과 슬릿 상단부의 아주 작은 영역을 통과한 파를 고려하면 스크린 상 의 한점 P까지의 경로차는 a/ 2 sin ( = slit의 폭)
만일 이 경로차가 /2와 같으면 소멸간섭(상쇄간섭)이 일어나고 2개의 영역 바로 밑에 있는 부 분으로 부터 나온 파도 반주기의 위상차를 가지므로, 슬릿의 상반부와 하반부에서 나오는 모든 빛이 서로 소멸간섭을 하여 어두운 줄무늬를 스크린상에 형성한다.
(a/2) sin = /2 sin = /a이면 소멸간섭함을 알수 있다. 또한 스크린을 4등분, 6등분하여 마찬가지 방법으로 생각하면 sin = 2 /a , 3 /a ,… 등일 때 소멸간섭을 하므로 일반화하여 sin = n /a , n=1, 2, 3, … 일 때 소멸간섭을 한다고 할수 있다.

키워드

빛,   이중슬릿,   간섭,   회절,   실험,   예비