경제성 공학에 대한 전반적인 이해

소개글

경제성 공학에 대한 전반적인 이해에 대한 보고서 자료입니다.

목차

1. 서론

2. 기초적인 경제개념

3. 등가계수와 등가계산

4. 인플레이션과 등가계산

5. 투자 대안의 선정

6. 대안평가 및 의사결정 방법의 활용

본문내용

현가의 변화를 나타내었다. 마찬가지로 예상수익 A의 변화에 따른 현가 변화와 투자기간 n의 변화에 따른 현가 변화를 각각 <표 6.4>,<6.5>에 나타내었다.
<표 6.4> A의 변화에 따른 현가 변화 추이
A(천원)
연간등가변동
P(천원)
현가변동
1,050
1,200
1,350
1,500
1,650
1,800
1,950
-30%
-20%
-10%
0
10%
20%
30%
-1,548
-626
295
1,217
2,139
3,060
3,982
-227%
-151%
-76%
0%
+76%
+151%
+227%
<표6.5> 기간(n)의 변화에 따른 현가 변화 추이
기간(년)
기간변동
P(천원)
현가변동
7
8
9
10
11
12
13
-30%
-20%
-10%
0%
10%
20%
30%
-697
2
639
1,217
1,743
2,221
2,655
-157%
-100%
-48%
0%
+43%
+82%
+118%
1) 현가가 양의 값을 갖기 위해서는 이자율의 변화가 추정치의 + 30%(즉 I=13%) 이내거나, 투자의 지속기간이 추정치의 -20%인 8년 이상, 연간 수익은 추정치의 -10%인 1,350,000원 이상 유지되어야 함을 알 수 있다.
2) 연간 수익의 경우 현재 추정치는 1,500,000원이나 경제 상황의 변화로 연간 예상 수익이 1,350,000원 까지 줄어들어도 투자의 타당성이 보장되고 있음을 알 수 있으며(이자율 및 투자기간이 변하지 않은 경우), 이자율 및 투자기간의 변화에 대하여도 유사한 해석을 할 수 있다.
3) 현가에 영향을 미치는 세 가지 변수 중 연간수익의 변화가 현가에 미치는 영향이 가장 큼을 알 수 있으므로, 이러한 투자를 계획하는 경우에는 연간 수익의 추정이 정확한 지를 특히 엄밀히 검토해 볼 필요가 있다.
4) 민감도 분석을 실시할 경우, 투자의 의사 결정을 정확히 하는 데에 많은 도움을 받을 수 있으며 투자된 사업의 운영을 위한 지침을 결정하는 데에도 참고자료가 된다. 따라서 사업을 위한 투자계획을 작성 할 때에 대부분 이러한 민감도 분석을 함께 실시하게 된다.
6.3 최적화문제
6.3.1 최적화의 개념
투자에 있어서 일반적으로 고려하는 사항은, 소요되는 비용을 최소화하거나 투자로 인하여 발생되는 이익을 최대화하는 것이다.
최적화(optimization) : 투자와 관련된 특정 변수 값의 조절을 통하여 비용을 최소 화하거나 이익의 극대화를 달성하는 것
임의의 변수를 ｘ로 나타내면, 변수 ｘ에 비례하는 비용( C1 )과 반비례하는 비용( C2 )은 일반적으로 다음과 같이 나타낼 수 있다.
C1 = ax + b (6.3)
C2 =
{ c} over {x }
+ d (6.4)
여기서 ｘ는 공통변수, ａ,ｂ,ｃ는 임의의 상수를 나타낸다.
따라서 총 비용은
CT = ax + b +
{c} over {x }
+ d
로 주어지는데, 총비용을 최소화하는 ｘ값은 CT 를 ｘ에 대하여 미분함으로써 구할 수 있다.
{ dC_{T}} over {dx }
= a -
{ c} over {x^{2} }
= 0
즉
x =
LEFT ( { c} over {a } RIGHT )^{1/2}
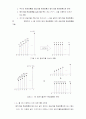
으로 주어진다. 한편 그래프에 의하여 최적 값을 구할 수도 있다. 즉 공통변수 ｘ에 따른 비용의 변화(식(6.3)과 식 (6.4))를 그래프로 나타내면 [그림6.5]와 같이 주어지므로, 이로부터 비용을 최적화하는 변수 값 ｘ를 구할 수 있다.
[그림6.5] 비용을 최소화하는 최적 변수 X값
예제6.5 소형 냉장고를 생산하는 전자회사에서, 냉장고 생산에 따른 비용을 분석해본 결과 냉장고 1대 당 소요되는 변동비는 47,730+100P 원으로 계산되었다. P는 냉장고의 일일생산량을 나타낸다. 또한 냉장고 생산시설과 관련한 고정비는 1,750,000원/일이며, 기타 고정생산비용은 7,325,000원/일으로 분석되었다. 냉장고의 판매가격이 대당 173,000원일 경우, (a) 냉장고 생산비용을 최소화하기 위한 일일 생산량을 결정하고 그때의 이익을 계산하시오. (b)일일 이익을 최대화하기 위한 일일 생산량을 결정하고 그때의 이익을 계산하시오. (c) 손익분기점이 되기 위한 일일 생산량을 결정하시오.
(풀이) (a) 생산비용을 최소화하기 위한 일일 생산량
냉장고 한 대 당 생산비용(TC)은 변동비와 고정비로부터,
TC=47,730 + 100P1.2 + (1,750,000 + 7,325,000)/P
으로 주어진다. 따라서 총비용을 일일 생산대수 P 에 대하여 미분하여 풀면,
{ dTC} over {dP }
= 0 =120P0.2 -
{ 9,075,000} over {P^{2} }
으로부터, 생산비용을 최소화하기 위한 일일생산량 P=165대임을 알 수 있다.
이때의 일일 총 이익(total profit per day) TP를 구하면,
TP =
LEFT [ 173,000-47,730-100(165)^{1.2}- { 9,075,000} over {165 } RIGHT ](165)
= 4,040,000원이다.
(b) 일일 이익을 최대화하기 위한 일일 생산량
생산대수가 P일 경우의 일일 총 이익은
TP =
LEFT ( 173,000-47,730-100P^{1.2}- { 1,750,000 + 7,325,000} over {P } RIGHT )P
의식으로 주어지므로, P에 대하여 미분하여 풀면,
{ dTC} over {dP }
= 0 = 125,270 - 220P1.2
으로부터, P=198대/일을 생산할 경우 일일 총 이익이 최대가 됨을 알 수 있으며, 그 값은
TP =
LEFT [ 173,000 - 47,730 - 100(198)^{1.2}- { 9,075,000} over {198 } RIGHT ](198)
= 4,400,000 이 된다.
(c) 손익분기점이 되기 위한 일일 생산량
손익분기점에서는 일일 총 이익과 총 비용이 같아지므로,
173,000P =
LEFT ( 47,730 + 100P^{1.2}+ { 1,750,000+7,325,000} over {P } RIGHT )P
으로부터, 손익분기점에서의 생산량은 P=88대/일 임을 알 수 있다.

키워드

경제성공학,   공학경제,   공학프로젝트,   경제개념,   경제공학공식풀이,   경제공학문제풀이