인지 발달 단계 이론과 수학 학습

소개글

인지 발달 단계 이론과 수학 학습에 대한 보고서 자료입니다.

목차

1. J. Piaget의 수학 학습 이론

2. J. Bruner 의 발견 학습

3. R. Gagne와 학습 위계 이론

4. Ausubel의 유의미적 수용 학습 이론

본문내용

지 않고도 내면화되어 의미 있게 적용될 수 있으므로 발견하는 활동이 개념이나 규칙의 내면화에 선행될
이유가 없다.
발견 학습은 그 나름의 정교성을 가지고 있으나 일정한 한계를 넘어서면 그
적용과 효과에 대한 기대가 미치지 못하는 때가 있고, 지식의 체계적인 습득이 곤란하며 시간이 많이 걸릴 가능성이 있다.
<표 6> 구 분
지식의 구조
인지 구조
주 창 자
Bruner
Ausubel
내 용
학문의 기저를 이루는 기본 개념과 원리, 핵심적 아이디어
어느 한 시점에서 학습자가 유용하게 사용할 수 있는 사실, 개념, 원리 및 이론 등으로 이루어진 지식체
위계적 구조
수학 개념이나 정리들이 상호 연관된 위계적 구조라서 수학적 지식의 구조를 명료하게 해준다.
하위 개념에서 점점 더 추상적, 포괄적 개념으로 위계구조가 형성됨
특 징
일반적인 아이디어, 원리로서의 지식의 구조를 강조함
학습자의 인지구조가 위계적이므로 개념원리를 먼저 제시하고 그 후에 특수한 예를 보이는 순서로 학습해야 한다.(연역적 계열을 옹호함)
브루너의 지식의 구조와 오스벨의 인지 구조 비교
(4) 유의미 학습의 전제 조건
학습자의 유의미 학습 태세
- 주어진 수학내용을 이해하려고 하며, 새로이 학습하는 내용을 이미 학습한
내용에 적용 또는 관련지으려는 태도를 갖추고 있는 경우
학습 자료의 잠재적 유의미가
- 학습자가 학습될 새로운 자료를 이미 아는 것에 관련지을 수 있도록 관련
정착 의미나 경험이 있어야 한다. 학습할 대상이 갖는 속성과 조직된 방법, 학습자마다의 고유한 인지 구조가 좌우
- 실사성: 한 과제를 어떻게 표현하더라도 그 과제의 의미가 변하지 않는 것
‘정삼각형은 세변의 길이가 같은 삼각형이다’ → ‘세변의 길이가 같은 삼각형은 정삼각형이다.’
- 구속성: 일단 임의적으로 맺어진 관계가 하나의 관습으로 굳어진 후에는 그 관계가 다시 임의로 변경될 수 없는 성질
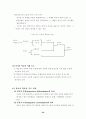
<그림 15> 유의미 학습의 조건
(5) 유의미 학습의 저해 요소
학습자가 수학의 특정 내용에 대한 유의미 학습에 필요한 지적 발달 수준에
도달하지 못한 경우
학습자가 유의미하게 학습을 수행하기에 충분히 동기 유발이 안 된 경우
교사가 자신이 지도할 내용이나 방식이 학습자에게 유의미할 것이라 잘 못
생각하는 경우
4.2 유의미 학습의 지도 원리
(1) 점진적 분화(progressive differentiation)의 원리
교과의 가장 포괄적이고 일반적이며 설명력이 있는 통합 개념과 원리를 먼저
제시하고 점차 특수화되고 세분화되는 방향으로 분화, 구체화하여 조직하는
원리.
(2) 통합적 조정(integrative reconciliation)의 원리
새로운 학습 내용과 이미 학습된 내용의 유사성과 차이점을 분명하게 하여 새
로운 학습 내용이 인지 구조 내에서 의식적으로 조정되고 명확히 분별되어 통
합되도록 하는 원리.
3) 선행 조직자(advanced organizer)의 원리
점진적 분화의 원리와 통합적 조정의 원리를 전개하기 위한 구체적인 교수
전략
새로운 학습 과제보다 추상성, 일반성, 포괄성의 정도가 높은 자료로 새로
운 학습 과제 제시에 앞서서 제시하는 자료로서 새로운 학습 내용을 이전
에 배운 내용과 연결, 통합, 설명해주는 것이다.
③ 선행 조직자의 종류
<표 6> 선행 조직자의 종류
종 류
적용 범위와 원리
주요 기능
설명 선행 조직자
비교적 생소한 내용 : 점진적 분화의 원리
정착 의미, 포섭
비교 선행 조직자
비교적 친숙한 내용 : 통합적 조정의 원리
인지적 다리, 변별
★ 설명 조직자의 예
“직각 삼각형”의 성질에 대한 학습에 앞서 일반적으로 삼각형이란 무엇이며
어떤 성질을 갖는지를 설명하는 것.
★ 비교 조직자의 예
“입체도형을 배우면서 그 전에 배웠던 평면도형과 비교한다.”
♠ 선행 조직자 모형을 적용한 수업 방법의 예
“덧셈과 뺄셈의 교환 작용의 의미”를 가르치기 위해 선행 조직자로서 국어의 “활동-반대 활동”을 먼저 도입한다.
<활동 1> 다음 빈 곳에 활동이나 반대 활동을 채워 넣어라
일어서다 - 앉다 / 시작하다 - 멈추다 / 열다 - 닫다
<활동 2> 수학의 경우에도 활동과 반대 활동이 있다.
(a) 8에 3을 더한 다음, 다시 3을 빼면 얼마인가?
8 + 3 -3 = ?
(b) 10에서 6을 뺀 다음 다시 6을 더하면 얼마인가?
10 - 6 + 6 = ?
(c) 6+4가 6이 되게 하려면 어떻게 해야 하는가?
4) 내용의 체계적 제시의 원리 : 학습효과의 극대화를 위해서는 학습 내용이
계열적, 체계적으로 조직되어야 한다. (연결성)
4.3 Ausubel의 선행조직자 수업 모델
<표 8> Ausubel의 선행조직자 수업 모델
단 계
활동 내용
1단계
선행 조직자 제시
수업 목표를 분명히 한다.
선행조직자를 제시한다.
학습자가 지니고 있는 사전 지식과 경험을 현재 수업 내용과 연결짓도록 자극한다.
학습 의욕을 고취시킨다.
2단계
학습 과제
및
자료의 제시
학습과제의 구속성과 실사성을 분명히 한다.
학습 자료의 논리적 조직을 명확히 한다.
자료를 제시한다.
점진적 분화의 원리 적용
3단계
학습자의
인지 조직 강화
적극적 수용 학습의 조장
통합 조정의 원리 이용하기
학습 내용에 대한 비판적 접근 유도하기
학습 내용 명료화하기 (정리)
◆ 참고문헌 ◆
강완, 백석윤 (1998). 초등수학교육론. 서울: 동명사.
강지형 (1999). 초등수학교육. 서울: 동명사
계영희, 김진숙 (2003). 우리 아이 수학 가르치기. 서울: 경문사
구광조, 오병승, 전평국(공역) (1995). 수학학습심리학. 서울: 교우사.
김용태, 박한식, 우정호 (1984). 수학 교육학개론. 서울: 서울대학교 출판부.
린 D. 잉글리쉬, 그레엄 S (2003). 수학교육론. 서울: 경문사.
우정호 (2000). 수학 학습-지도의 원리와 방법. 서울: 서울대학교 출판부.
이숙례 (1981). 현대 초등 수학 교육론. 서울: 이화여자대학교 출판부.
Bruner, J. (1965). Toward a theory of Instruction. New York: W. Norton Co.

키워드

피아제,   브루너,   가네,   아수벨,   인지,   수학,   발달,   학습