아레니우스

본문내용

{dC} over {C^2} ~=~ INT _{ o}^{t } -kdt
, 따라서 농도는
1 over C ~=~ {1 over C_o} ~+~ kt}
가 된다.
반응 시간(횡축)과
1 over C
(종축)를 그려 직선이 되는지 여부를 확인하여 직선이 되면 위 반응은 2차 반응이 된다. 마찬가지로 직선식의 기울기가 반응속도상수(k)가 된다.
▷ A + B --> P (반응물이 2개, 비가역 반응)와 같은 반응이 진행되는 경우 반응속도식 도출과정을 살펴보면 다음과 같다. 우선 이 반응이 기본반응이라면 반응속도식은 다음과 같이 표현될 수 있다.
r_A ~=~ r_B ~=~ -k C_A C_B ~=~ dC_A over dt ~=~ dC_B over dt
① 두 반응물의 초기 농도가 같은 경우(
C_{A_O} = C_{B_O}
)
두 반응물의 초기 농도가 같고 위 반응식에서 A와 B는 1:1로 반응하여 생성물로 되기 때문에 일정시간 t가 지난 후에 남아 있는 A와 B의 물질 농도는 동일하다. 따라서 반응속도식은
dC_A over dt ~=~ -kC_A^2
으로 쓸 수 있다. 그러면 A에 대해 2차 반응이므로 그림 3과 같이 2차 반응으로 해석할 수 있다.
② 두 반응물의 초기 농도가 다른 경우(
C_{A_O} != C_{B_O}
)
반응물의 초기 농도가 다르기 때문에 t 시간 후 남아 있는 반응물의 농도도 다르다. 따라서 t 시간 동안 반응에 의해 없어진 반응물의 농도를 X라 두면 남아 있는 반응물의 농도는 다음과 같이 정리된다. 즉
C_{A} ~=~ C_{A_O} ~-~ X
,
C_{B} ~=~ C_{B_O} ~-~X
가 된다. 이 식을 미분하면
dX over dt ~=~ - {dC_A over dt} ~=~- {dC_B over dt}
가 된다. 원래의 반응속도식에 X가 고려된 농도를 이용하면 다음과 같다.
dX over dt ~=~ - {dC_A over dt} ~=~- {dC_B over dt} ~= ~ k(C_{A_O} - X)(C_{B_O} -X)
위 식을 적분하면 다음과 같아진다. (부분분수로 분리하여 적분한다.)
INT _{ 0}^{X } dX over {(C_{A_O} - X)(C_{B_O} -X)} ~ = ~ INT _{ 0}^{t } k dt
ln{C_B over C_A} ~=~ ln{C_{B_O} over C_{A_O}} +(C_{B_O} - C_{A_O})kt
따라서
ln{C_B over C_A}
와 t를 그래프로 그리면 직선이 나오고 직선의 기울기는
{(C_{B_O} - C_{A_O})} k
이므로 반응속도상수 k값을 결정할 수 있다.
※ 따라서 위와 같은 경우에는 두 반응물의 초기 농도를 같게 놓은 후 반응을 진행시킨 후 결과를 속도론으로 해석하는 것이 더 간편함을 알 수 있다.
그림1
C_{A_O} = C_{B_O}
인 경우의 선형화 그림2
C_{A_O} != C_{B_O}
인 경우의 선형화
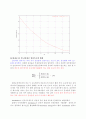
그림3 적분법으로 반응차수와 속도상수 결정
a) 1차 반응 b) 2차 반응

키워드

함수,   아레니우스,   아레