비누화 반응 실험

목차

1. 실험목적

2. 이론

3. 실험 장치와 시약

4. 실험방법

본문내용

-1.975
적분법
위의 식 (4)를 변형하면,
( { 1} over { a } - { 1} over { { a}_{ 0} }) = { K}_{1 }t
가 된다.
적분법에서도 시간에 대한
( { 1} over { a } - { 1} over { { a}_{ 0} })
의 그래프에서 기울기가
{ K}_{1 }
이 된다.
실험 30
실험 50
시간 (min)
t
a(=b)
da/dt 10-3
ab(=a2) 10-3
t
a(=b)
da/dt 10-3
ab(=a2) 10-3
0
1
0.05
-15.80
2.50
1
0.05
-4.93
2.50
1
1
0.0342
-5.40
1.17
1
0.0068
-2.40
0.4624
2
0.0288
0.83
0.0044
0.0194
1
-5.10
1
-1.76
3
0.0237
0.562
0.00264
0.00697
1
-3.60
1
-0.68
4
0.0201
0.404
0.00196
0.00384
1
-3.00
1
-0.32
5
0.0198
0.392
0.00164
0.00269
2
-1.05
2
-0.08
7
0.0177
0.313
0.00148
0.00219
3
-1.00
3
-0.093
10
0.0147
0.216
0.0012
0.00144
2
-1.90
2
-0.44
12
0.0109
0.119
0.00032
0.0001
3
-0.23
3
-0.013
15
0.0102
0.104
0.00036
0.0001
5
-0.42
5
0.0
20
0.0081
0.0656
0.00036
0.0001
5
-0.14
5
-0.008
25
0.0074
0.0547
0.00032
0.0001
5
-0.28
5
0.008
30
0.0060
0.0360
0.00036
0.0001
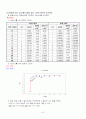
①
( { 1} over { a } - { 1} over { { a}_{ 0} })
를 t에 대하여 그려라.
적분법을 이용한 data 계산 및 그래프
30 일때 그래프
50 일때 그래프
②
{ K}_{1 }
의 값을 구한다.
식 (4)에서 보면
( { 1} over { a } - { 1} over { { a}_{ 0} }) = { K}_{1 }t
이므로 위의 그래프에서 기울기가
{ K}_{1 }
에 해당한다. 그러므로 적분법으로 구한 반응속도 정수 (실험 30
{ K}_{1 }
= 4.889 실험 50
{ K}_{1 }
=9.192)
실험 30
실험 50
시간 (min)
(1/a - 1/a0)
(1/a - 1/a0)
0
0
0
1
9.240
12.105
2
14.72
20.77
3
22.194
30.878
4
29.751
49.020
5
30.505
58.975
7
36.497
65.5672
10
48.027
81.333
12
71.743
310.5
15
78.039
275.777
20
103.458
275.777
25
115.135
310.5
30
146.667
275.777
30 일때 -
50 일때 -
③ 역반응이 무시될 수 있는 가를 검토하여라.
{ K}_{2 }
값을 계산하기 위해선 우선, 위의 (1)번 반응식에 해당하는
{H }_{f }
,
{ G}_{ f}
를 문헌에서 찾아보면,
화학식
{H }_{f }
{ G}_{ f}
CH3COOC3H5( )
-111.18
-102.02
NaOH
-101.30
-112.19
CH3COONa( )
-176.18
-175.45
C2H5OH( )
-66.63
-66.35
(단위,kcal/mol)
이고,
{ K}_{2 }
계산에 있어서 다음 식들이 사용된다.
{G }^{. } =RTlnK
(i)
■■
{H }^{. } =R { T}^{2 } { d(lnK)} over {dT }
(ii)
d(lnK)= { - {H }^{. } } over { R} TIMES d( { 1} over { T} )
(iii)
{H }^{. }
는 온도의 함수이지만 온도에 따라 크게 변하지 않으므로 T와 무관하다고 가정하면, 식 (iii)는
ln { K} over { { K}_{ 0} } = -{ {H }^{. } } over { R} TIMES ( { 1} over { T}- { 1} over { { T}_{0 } } )
(iv)
로 변형된다.
표준상태
{ T}_{ 0}
=25 =298.15K서
{ G}_{0 } =175.45-66.35-(-102.02-112.193)=-27.587 kcal/mol
을 가지고, 위 식 (i)에서 보면,
ln { K}_{ 0} = -{ {G }^{. } } over { RT} = { 27.587 TIMES 1000} over {298.15 TIMES 1.987} =46.57
{ K}_{0 } =1.6792 TIMES { 10}^{20 }
이번 실험은 25 로 맞추어진 항온조에 반응기를 넣어 실험하였으므로 식 (iv)에서,
( { 1} over { T}- { 1} over { { T}_{0 } } )=0
이므로,
lnK=ln {K }_{0 }
이다.
K=1.6792 TIMES { 10}^{20 }
반응 속도식에서보면,에서 [
{ K}_{2 }
=
{ K}_{1 }
/
K
]이다.
그러므로를
K
와
{ K}_{1 }
값을 대입하면,
미분법 :
{ K}_{2 } = { 6.298} over {1.6792 TIMES { 10}^{20 } }= 6.5859 TIMES { 10}^{ -20}
{ K}_{2 } = { 1.975} over {1.6792 TIMES { 10}^{20 } }= 6.5859 TIMES { 10}^{ -20}
적분법 :
{ K}_{2 } = {4.889} over {1.6792 TIMES { 10}^{20 } }=1.1897 TIMES { 10}^{-18 }
{ K}_{2 } = {9.192} over {1.6792 TIMES { 10}^{20 } }=1.1897 TIMES { 10}^{-18 }
이 나온다.
위에서 구한
{ K}_{2 }
의 값은
{ K}_{1 }
값에 비하여 충분히 작은값, 0에 가까운 값을 나타내므로 처음 가정했던 것처럼 평형상수의 정의에 의해 역반응은 무시할 수 있다.y

키워드

보고서,   비누화,   비누화 반응,   비누화 반응 실험,   실험,   실험 보고서